曲线y1=x^2与y2=(1/n)√x围成的面积

1、y1=x^2与y2=√x在直角坐标系的图像如下：

2、联立曲线方程y1=x^2与y2=√x，求出二者的交点：

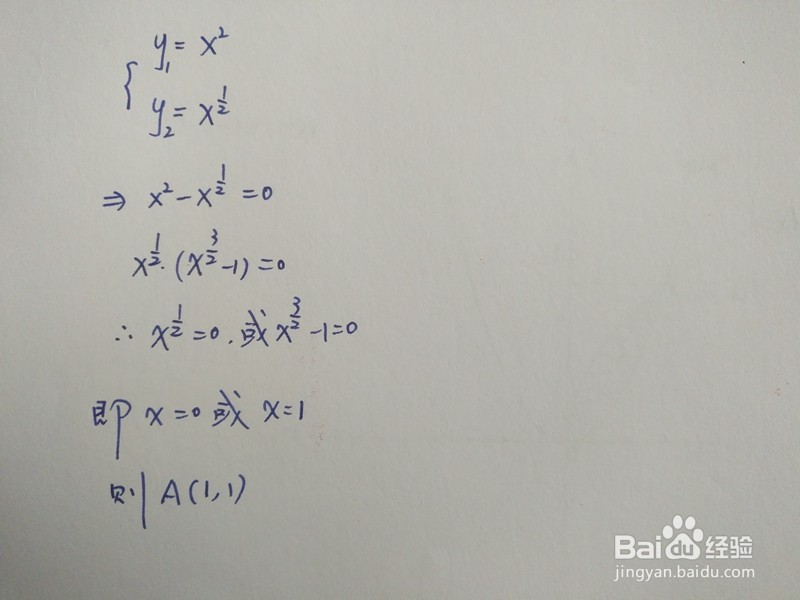
3、根据定积分面积公式，求出此时曲线围成的面积，主要步骤如下：

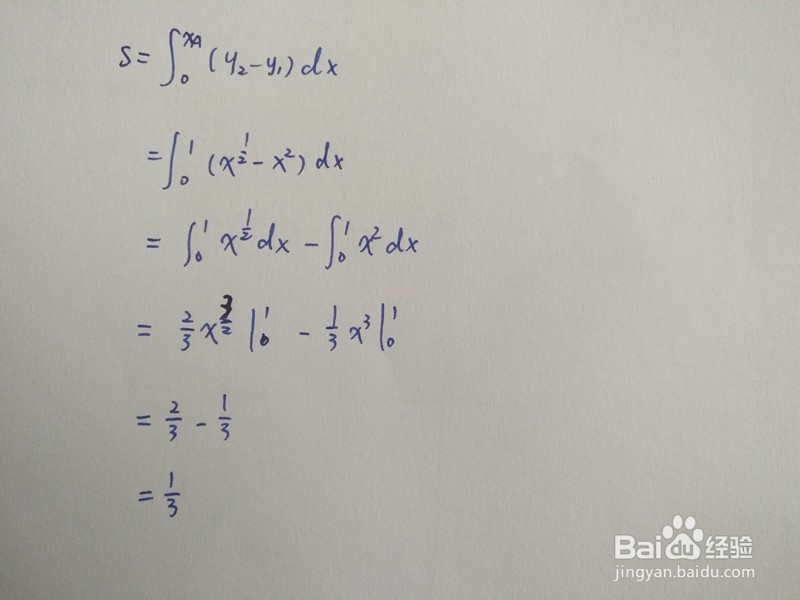
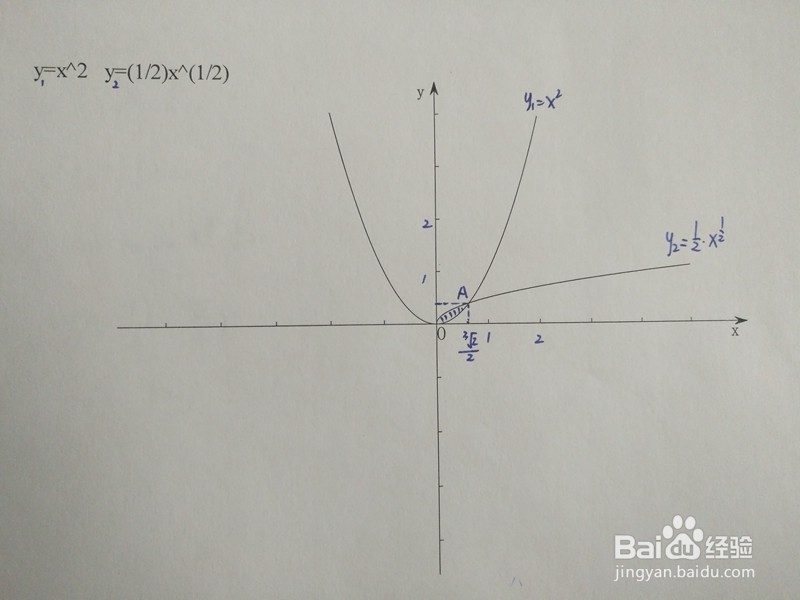
1、y1=x^2与y2=(1/2)√x在直角坐标系的图像如下：

2、联立曲线方程y1=x^2与y2=(1/2)√x，求出二者的交点：

3、根据定积分面积公式，求出此时曲线围成的面积，主要步骤如下：

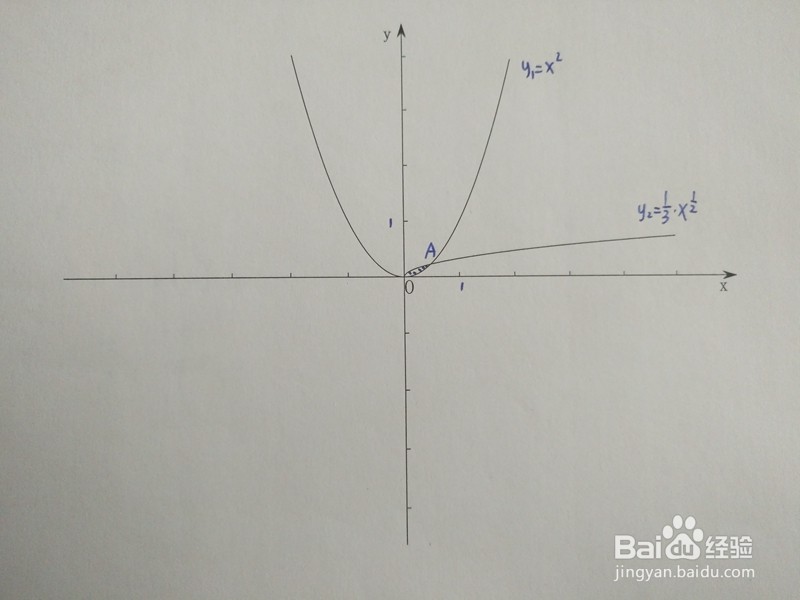
1、y1=x^2与y2=(1/3)√x在直角坐标系的图像如下：

2、联立曲线方程y1=x^2与y2=(1/3)√x，求出二者的交点：

3、根据定积分面积公式，求出此时曲线围成的面积，主要步骤如下：