python fipy 求解偏微分方程

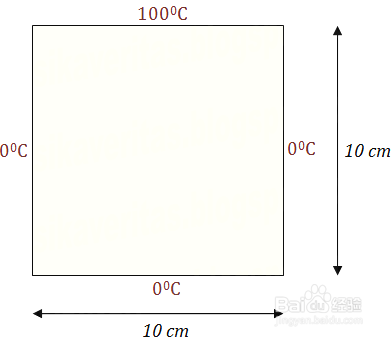
1、首先简介问题。一个二维平板，顶端1摄氏度（100也可以，只是一个系数），另外三个边缘0摄氏度，初始时刻整个板子都是0摄氏度，随之时间的推进，热量在板子上传递，最后达到平衡态，我们不仅希望知道平衡态的温度分布，也希望知道温度随时间是如何变化的。

如果这篇经验过于复杂者不够直接或者fipy无法安装，可以参考另一篇python偏微分方程经验  

jingyan.baidu.com/article/46650658d71872f548e5f852.html

12python有限差分求解拉普拉斯方程

2、热量的传递由微分方程给出，可以简单地理解为热量按照温度降低最快的方向进行传递。

公式右边是温度的梯度，左边是温度随时间的变化

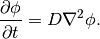
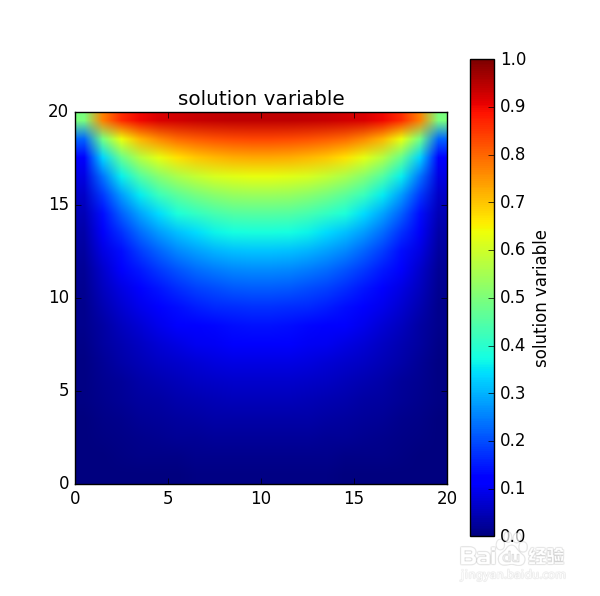
3、先看一张最后的结果过个瘾，也比较容易想象，最后整个板子的温度分布大致呈现怎样

4、只有一个包需要导入

import fipy as fp

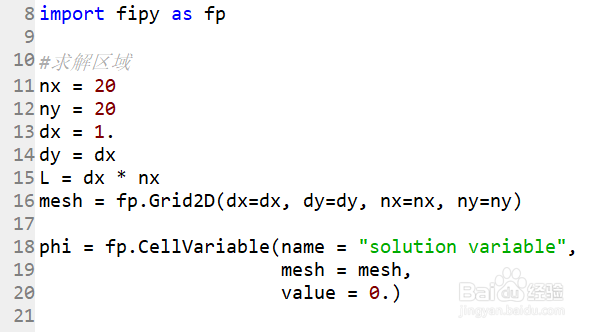
5、确定求解区域，一个20*20的格点

#求解区域nx = 20ny = 20dx = 1.dy = dxL = dx * nxmesh = fp.Grid2D(dx=dx, dy=dy, nx=nx, ny=ny)

phi = fp.CellVariable(name = "solution variable",                      mesh = mesh,                      value = 0.)

6、创建微分方程

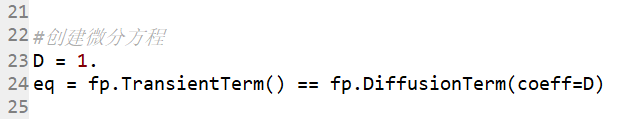
7、设立边界条件

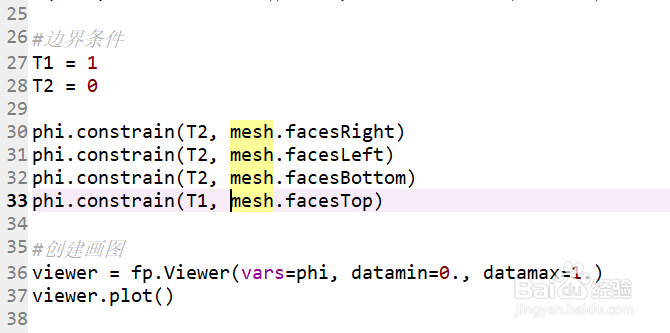
8、创建画图

9、求解

10、建议在命令行里面运行，命令行里面可以获得动图，ipython里面只有最后一张图

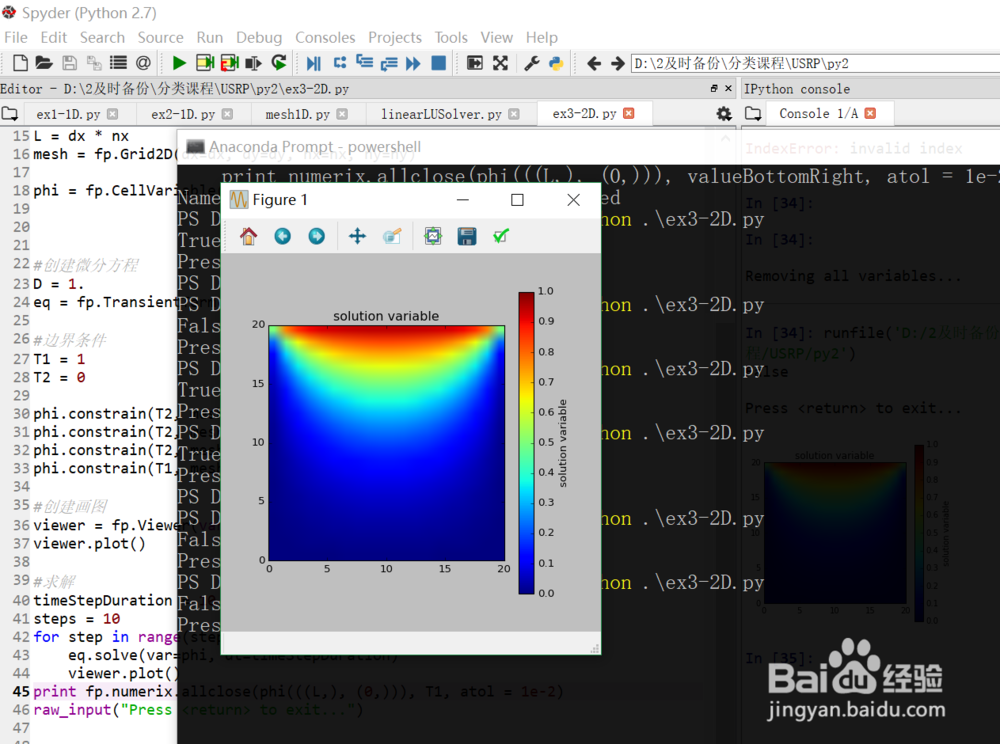
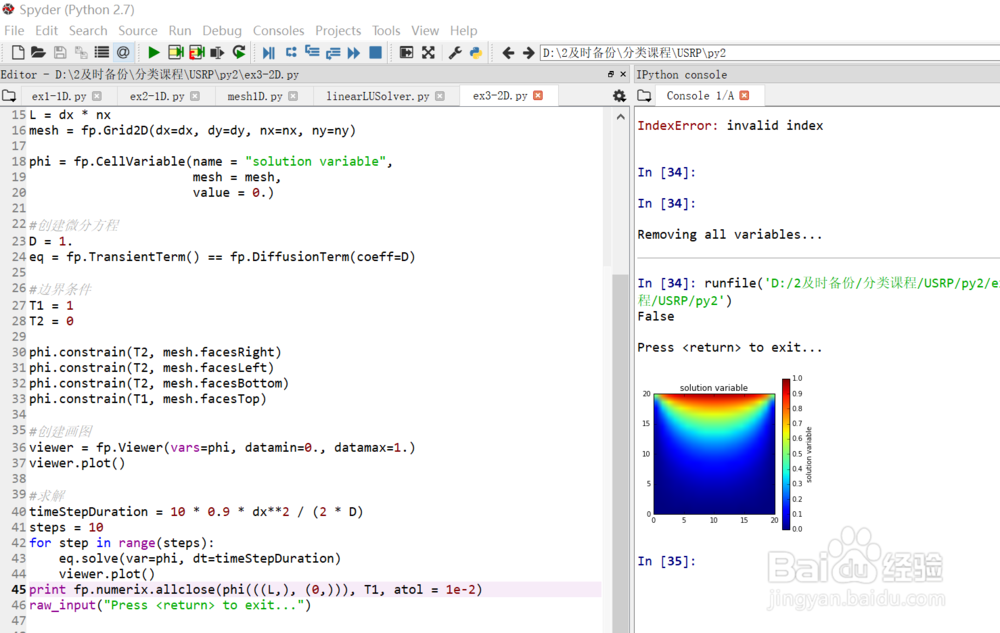
11、spyder的ipython里面只有最后的一张图片

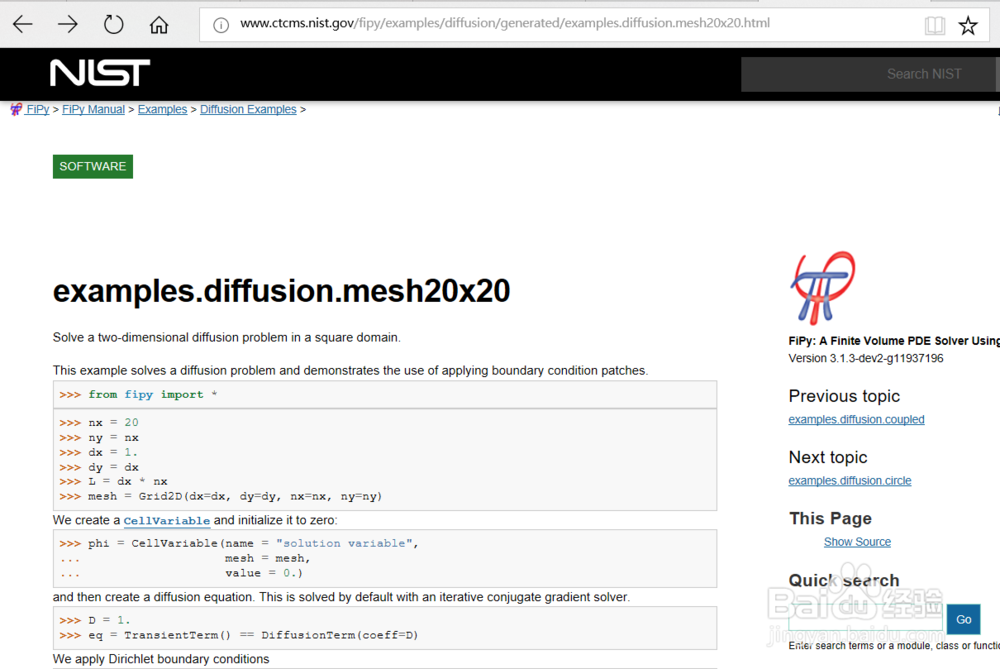
12、主要参考文章为fipy的官方示例                             

www.ctcms.nist.gov/fipy/examples/diffusion/generated/examples.diffusion.mesh20x20.html                                    

www.ctcms.nist.gov/fipy/examples/diffusion/generated/examples.diffusion.mesh1D.html#equation-eq:diffusion:mesh1D:constantD