求证：直角三角形的外接圆半径等于斜边的一半

1、这是数学中有关于几何图形（直角三角形和圆）定理的互相证明问题，一般初高中的同学会经常遇到。

1、这里涉及到两个长度概念，一是直角三角形的外接圆半径长度R，二是直角三角形斜边长度的一半，需要证明这二者的长度相等。可以直接用画图配合文字说明的方法来证明。

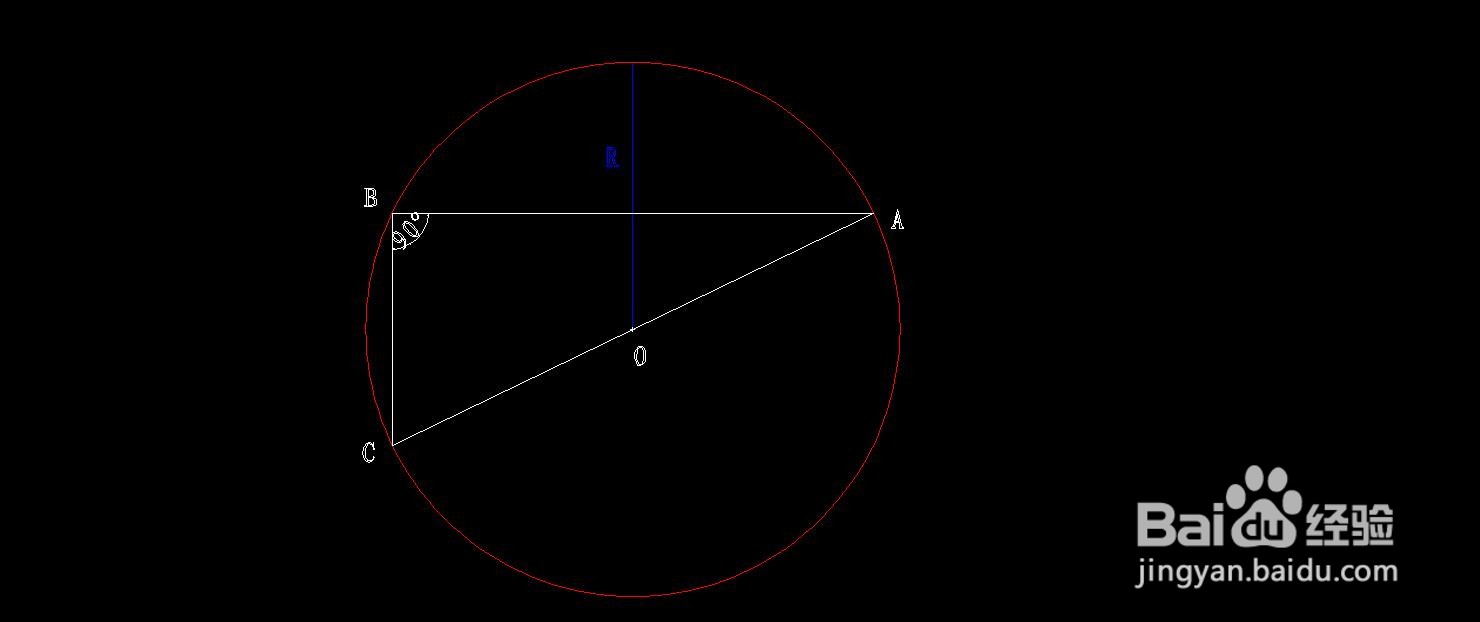
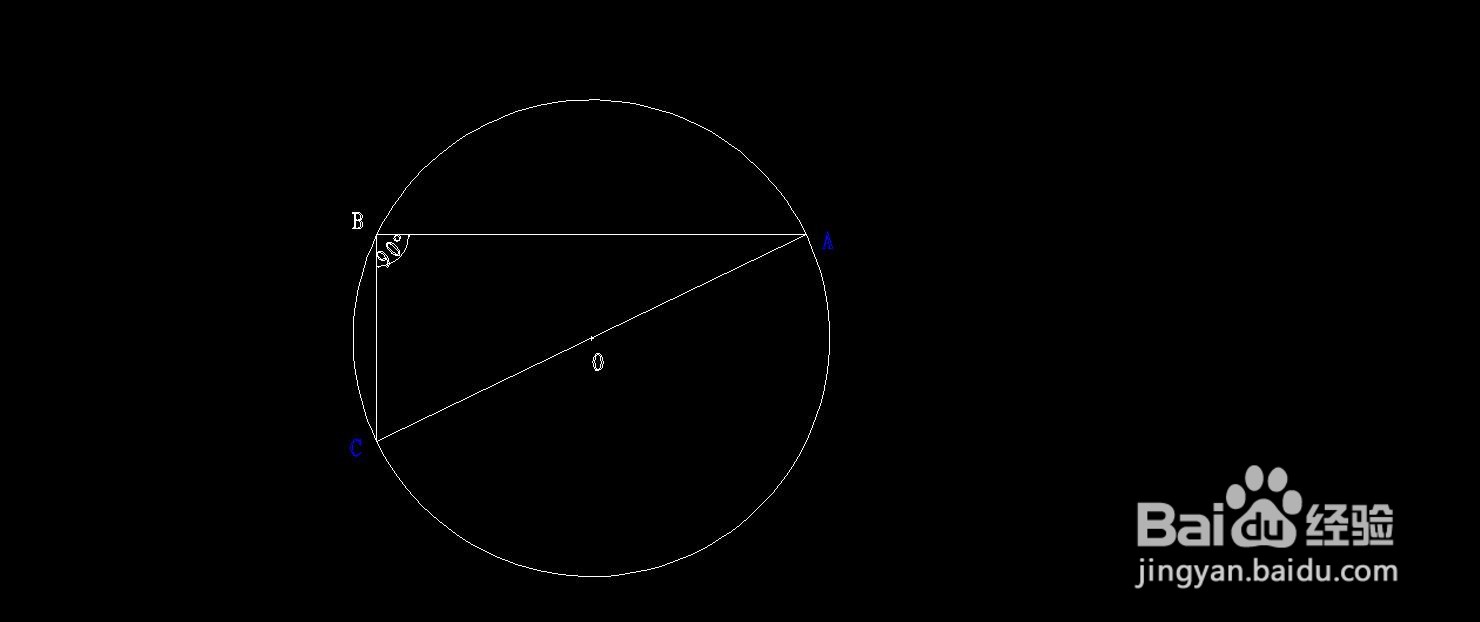
1、先画图，画图分两步完成。

①先画任意直角三角形。作以∠B为直角的任意直角三角形▲ABC；

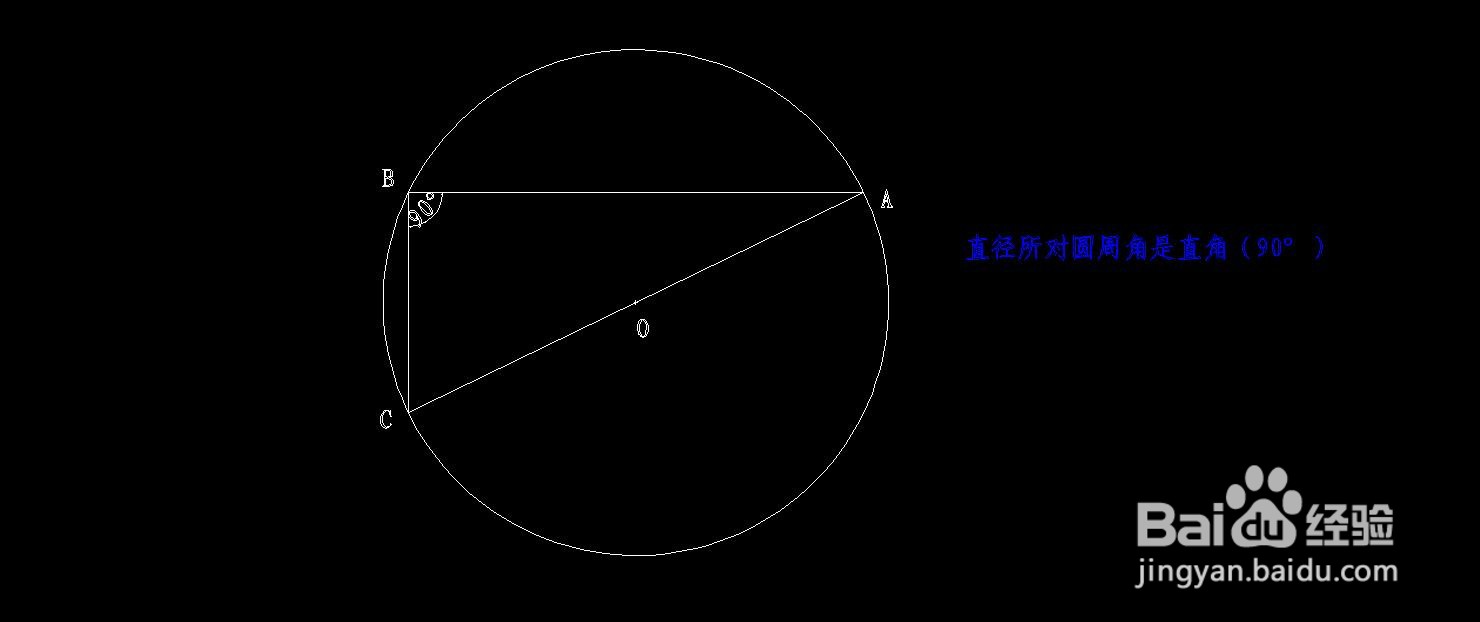
②再画出该直角三角形的外接圆。过直角▲ABC三个顶点A、B、C作圆心为O点的外接圆。

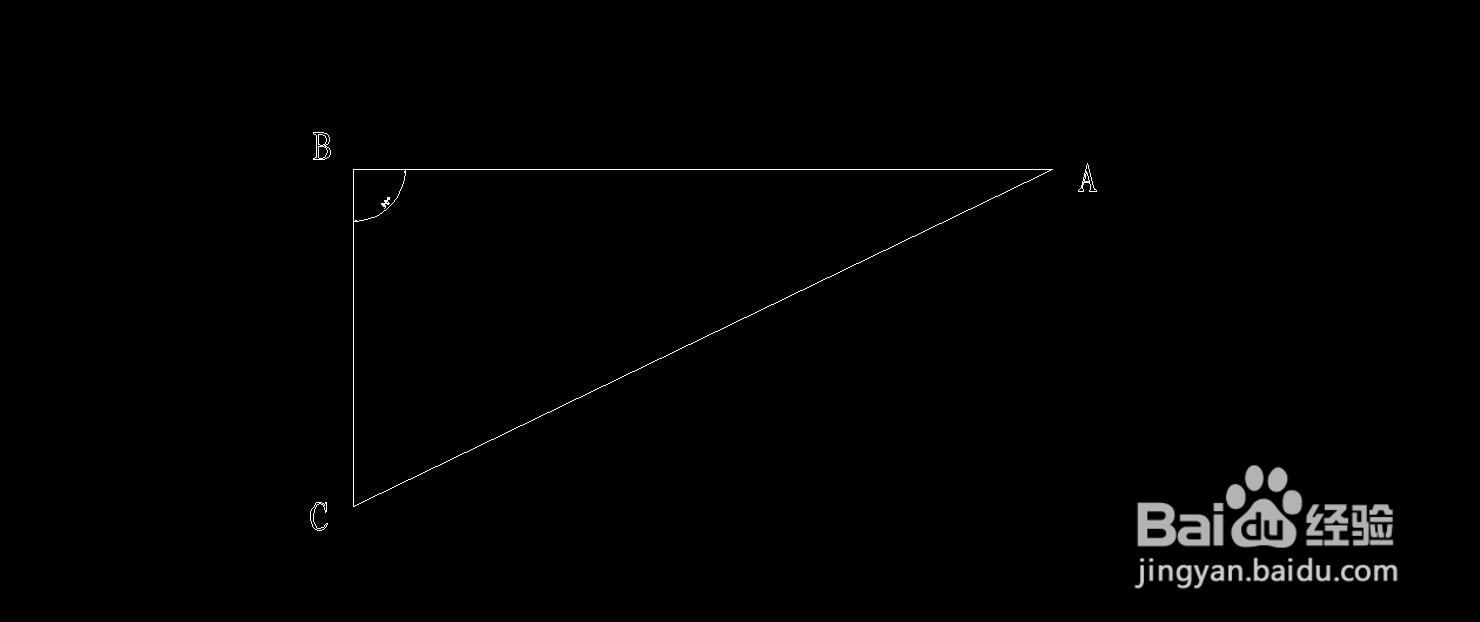
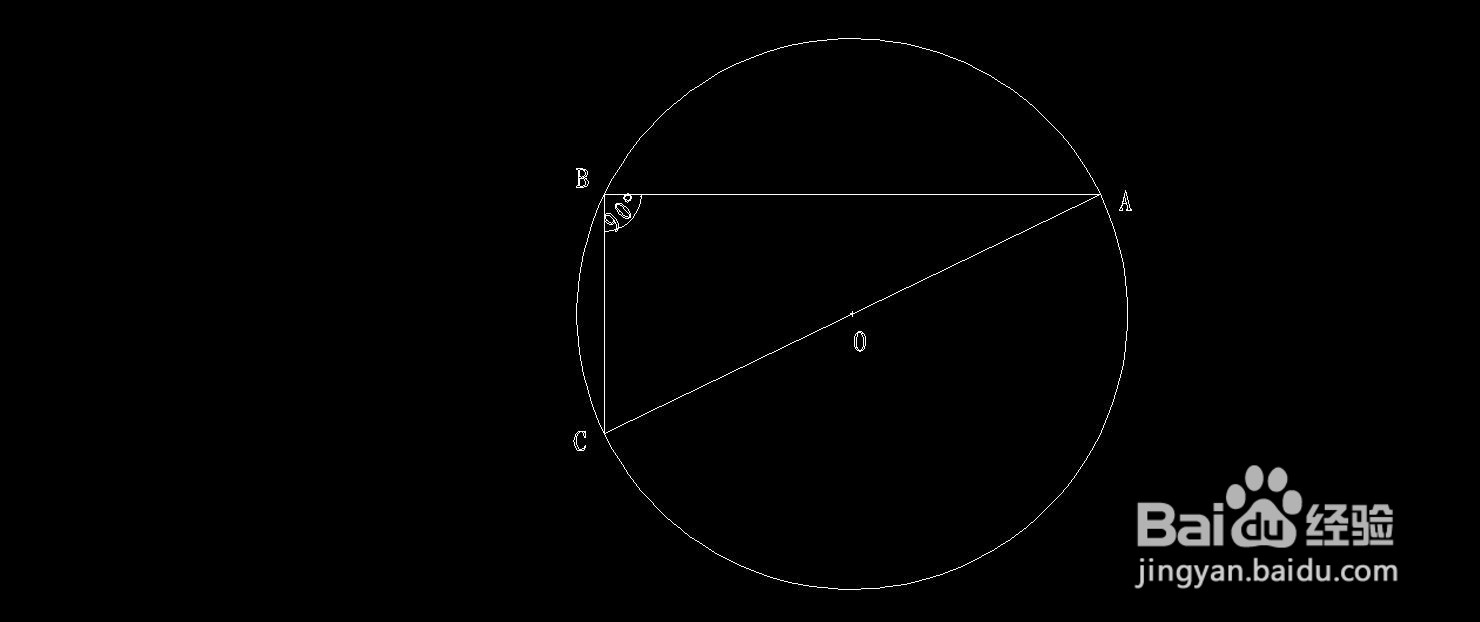
2、再证明：

∵任意半径为R的圆O的性质（直径所对的圆周角等于90°），

∴斜边AC即为圆O的直径，

∴斜边AC的中点即为圆的圆心O，

∴OA=OC=AC/2=R，

即得证，任意直角三角形的外接圆半径长度等于斜边长度的一半。

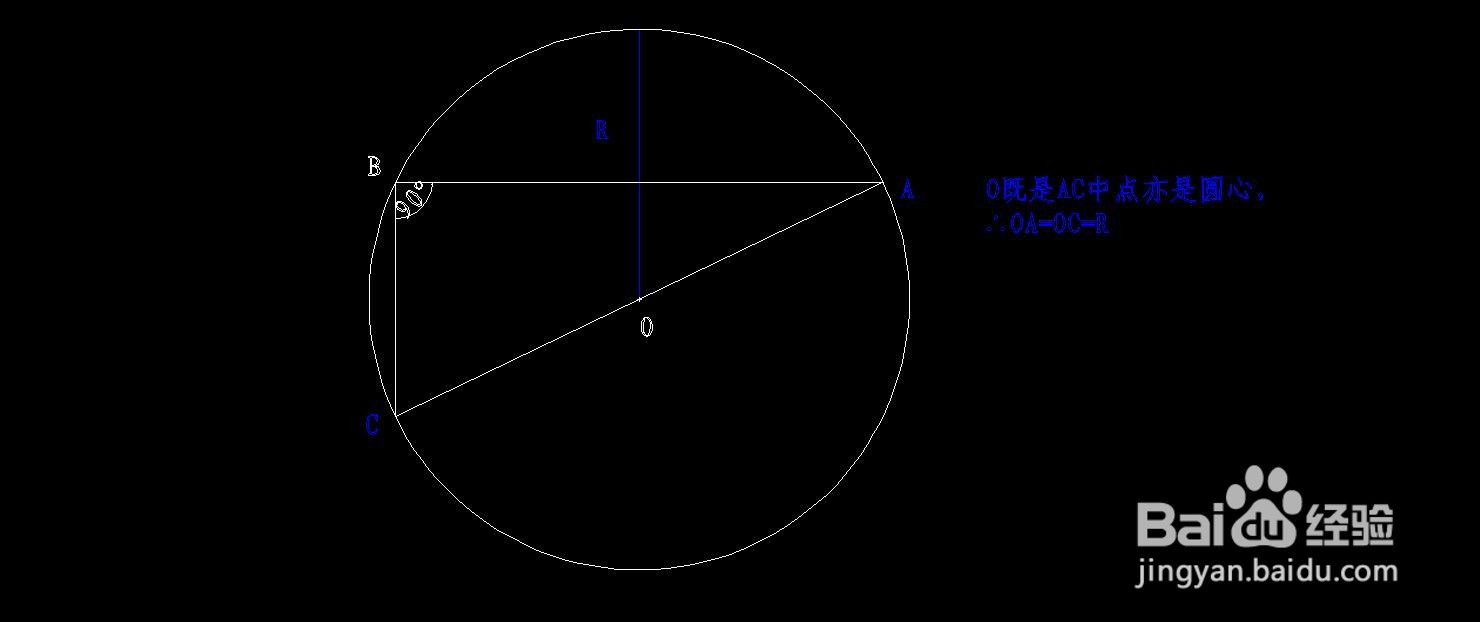
1、结论：任意直角三角形的外接圆半径长度等于斜边长度的一半。

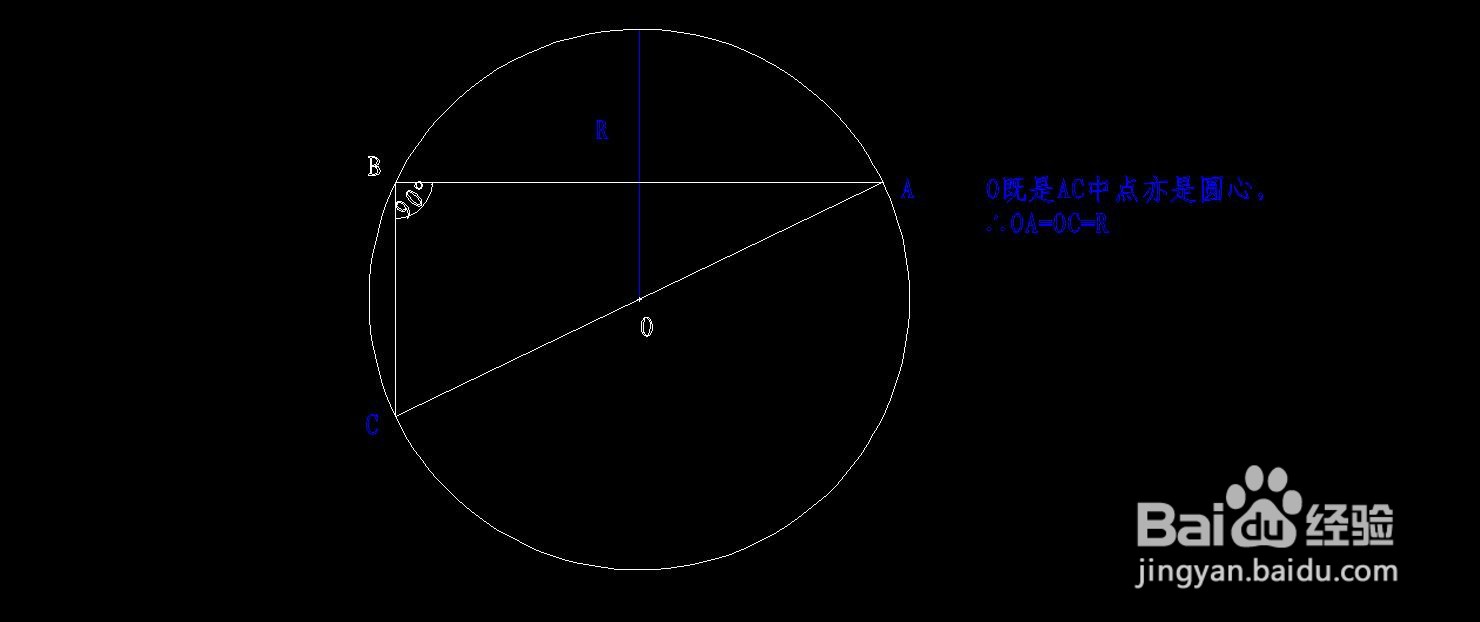
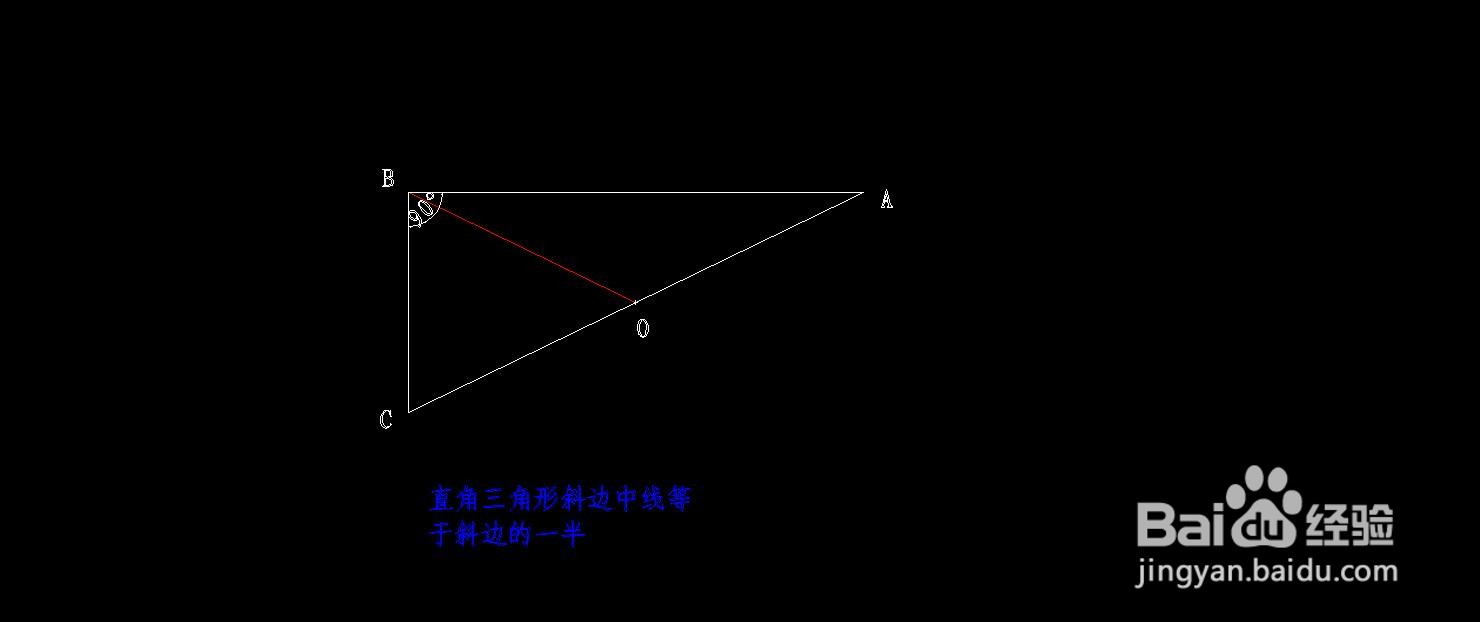
1、先连接OB，如下图所示。

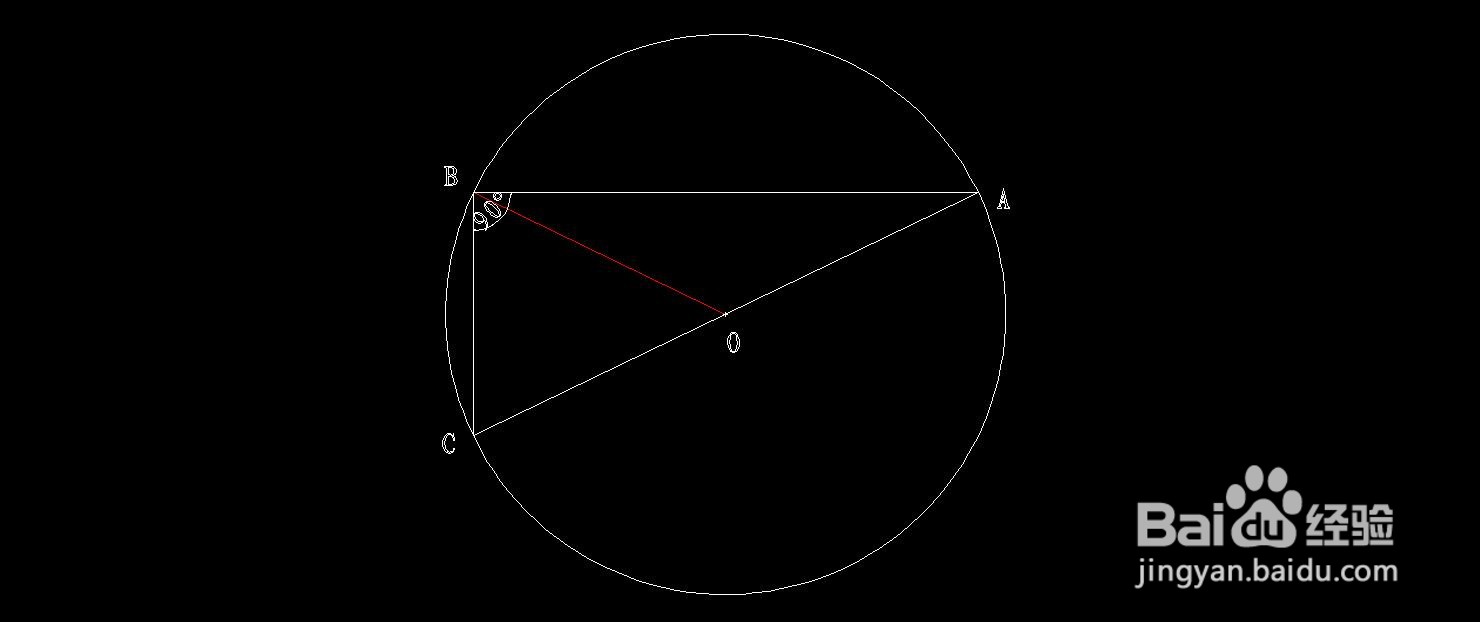
2、推论证明过程。

证明：

∵OB是▲ABC斜边AC的中线，

又∵OB是圆O的半径，

∴AC的中线OB长度即为圆半径长度R，

∴OB=OA=OC=AC/2=R，

∴任意直角三角形的斜边上的中线等于斜边的一半。

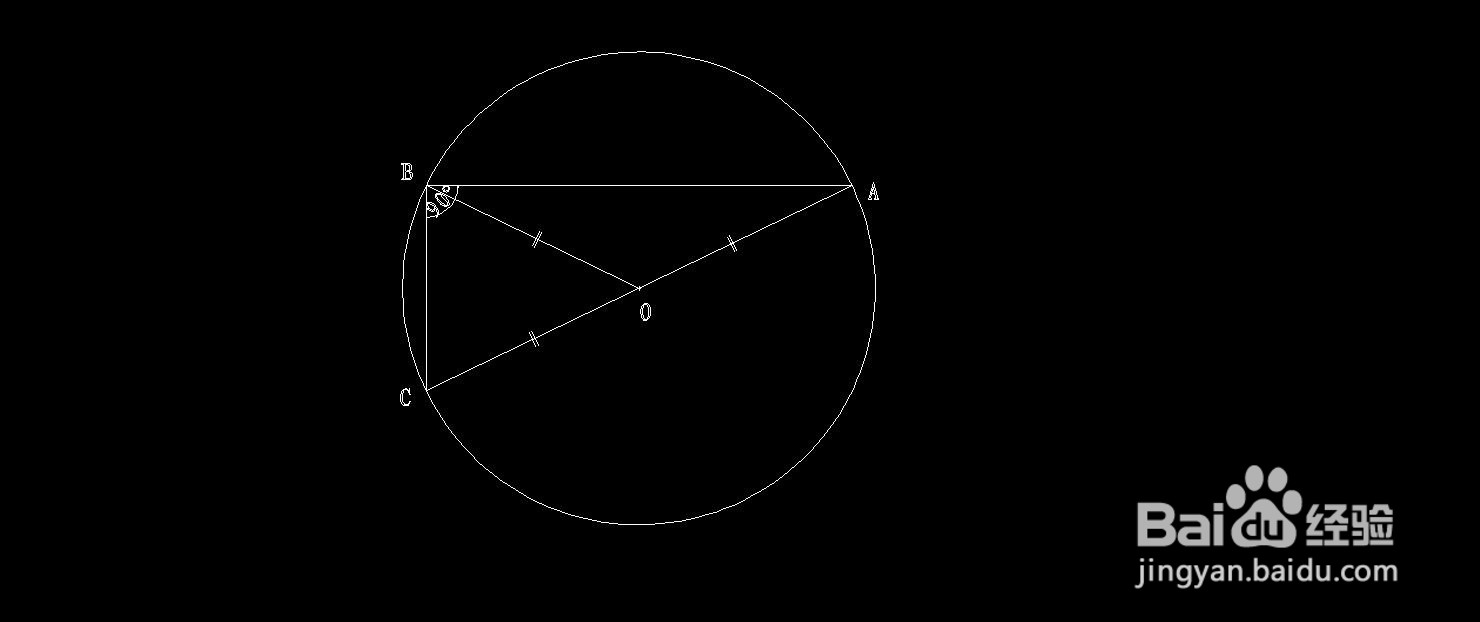
3、由结论得出推论。

由以上结论，任意直角三角形的外接圆半径长度等于斜边长度的一半。可以得出以下两条推论。

推论1：任意直角三角形的斜边上的中线长度等于斜边长度的一半。

推论2：推论1和圆的性质（直径所对的圆周角等于90°）可以互相证明彼此。