Mathematica基础——ContourPlot的选项（续）

1、        用PlotLegends来增加图形的图例：

ContourPlot[Sin[6 x + y] Cos[x - 6 y], {x, 0, Pi}, {y, 0, Pi}, 

             PlotLegends -> Automatic]

        等高线的数量越多，图例越多：

Table[ContourPlot[Sin[6 x + y] Cos[x - 6 y], {x, 0, Pi}, {y, 0, Pi}, 

       Contours -> c, PlotLegends -> Automatic], {c, {5, 10, 20}}]

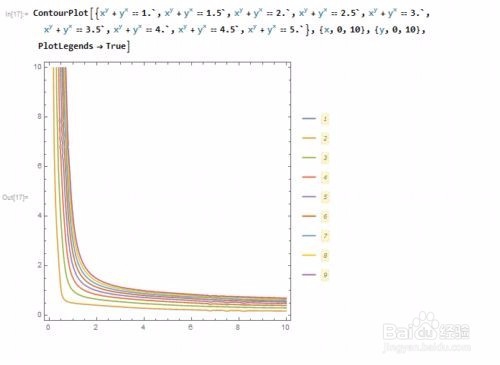
2、        当在一幅图里绘制多条隐函数图像时，可以给不同的图像，加上图例，并且颜色是相互匹配的：

ContourPlot[{x^y + y^x == 1.`, x^y + y^x == 1.5`, x^y + y^x == 2.`, 

  x^y + y^x == 2.5`, x^y + y^x == 3.`, x^y + y^x == 3.5`, 

  x^y + y^x == 4.`, x^y + y^x == 4.5`, x^y + y^x == 5.`}, {x, 0, 

  10}, {y, 0, 10}, PlotLegends -> True]

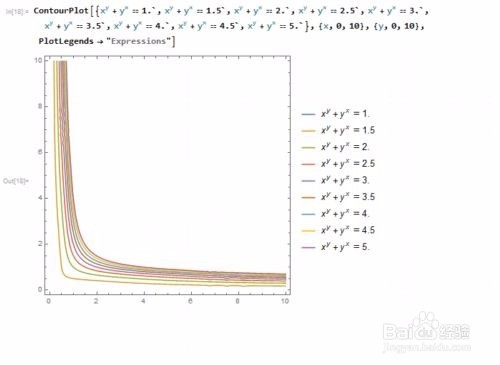
        或者用PlotLegends -> "Expressions"来把图例显示为具体的表达式：

ContourPlot[{x^y + y^x == 1.`, x^y + y^x == 1.5`, x^y + y^x == 2.`, 

  x^y + y^x == 2.5`, x^y + y^x == 3.`, x^y + y^x == 3.5`, 

  x^y + y^x == 4.`, x^y + y^x == 4.5`, x^y + y^x == 5.`}, {x, 0, 

  10}, {y, 0, 10}, PlotLegends -> "Expressions"]

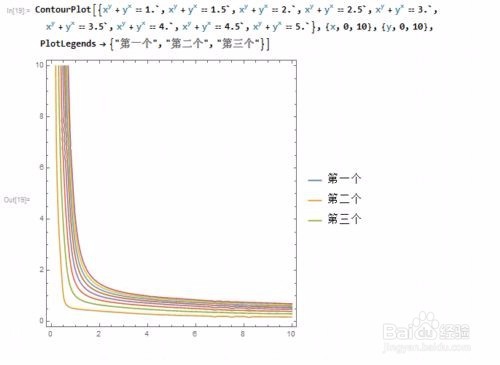
3、        还可以指定图例所要显示的内容：

ContourPlot[{x^y + y^x == 1.`, x^y + y^x == 1.5`, x^y + y^x == 2.`, 

  x^y + y^x == 2.5`, x^y + y^x == 3.`, x^y + y^x == 3.5`, 

  x^y + y^x == 4.`, x^y + y^x == 4.5`, x^y + y^x == 5.`}, {x, 0, 

  10}, {y, 0, 10}, PlotLegends -> {"第一个", "第二个", "第三个"}]

        后面的那些图的图例，大家可以自己写。

4、        用Placed可以改变图例放置的位置：

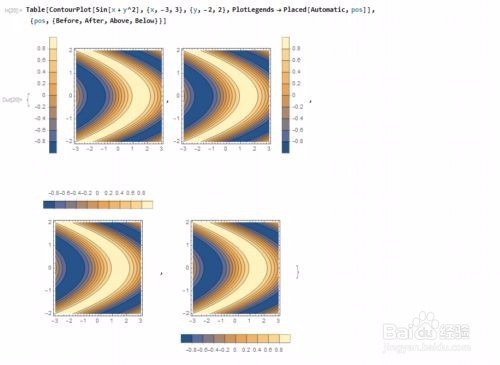
Table[ContourPlot[Sin[x + y^2], {x, -3, 3}, {y, -2, 2}, 

    PlotLegends -> Placed[Automatic, pos]], {pos,

       {Before, After, Above,Below}}]

        或

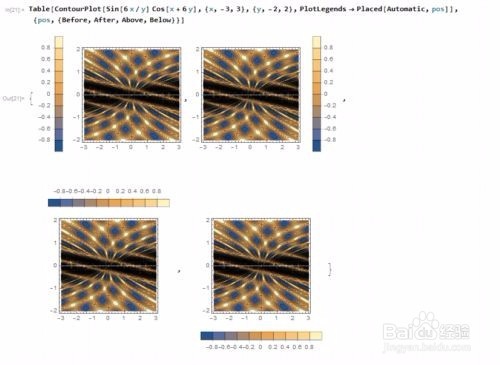
Table[ContourPlot[Sin[6 x/y] Cos[x + 6 y], {x, -3, 3}, {y, -2, 2}, 

  PlotLegends -> Placed[Automatic, pos]], 

    {pos, {Before, After, Above,Below}}]

        把图例非别放在前边、后边、上边、下边。

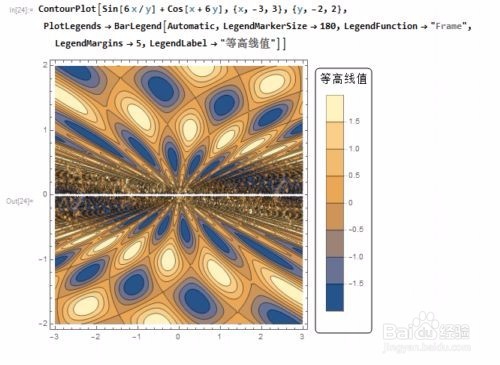
5、        用BarLegend（酒吧的传说）可以改变图例的具体样式，

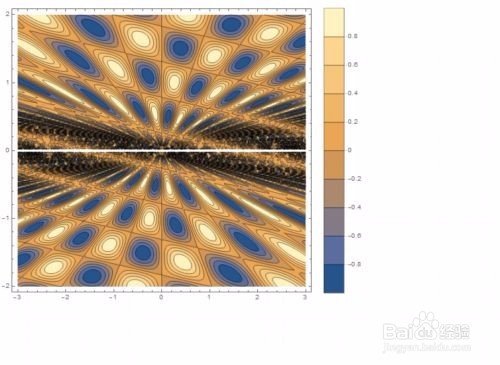
ContourPlot[Sin[6 x/y] + Cos[x + 6 y], {x, -3, 3}, {y, -2, 2}, 

 PlotLegends -> 

  BarLegend[Automatic, LegendMarkerSize -> 180, 

   LegendFunction -> "Frame", LegendMargins -> 5, 

   LegendLabel -> "等高线值"]]