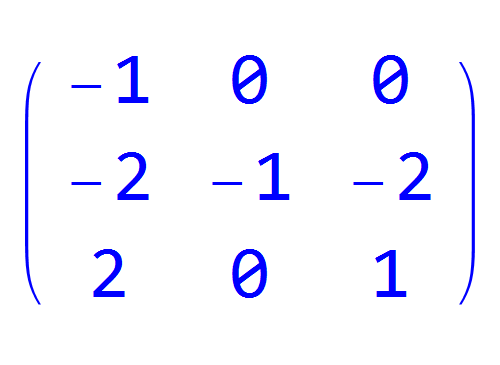怎么用计算机来构造一个简单的循环群？

1、当a={{1,1}, {0, -1}}，那么，a生成的循环群，共有六个元素：

MatrixForm[#] & /@ (Table[MatrixPower[a, n], {n, 1, 10}] // Union)

而且，a是这个群里面的一元，其阶数是6。

2、如果矩阵a的行列式大于1，那么a一般不会生成一个群：

a = {{1, 1}, {-1, 1}}

比如：

MatrixPower[a, 6]

3、对应的逆矩阵是：

MatrixPower[a, 6] // Inverse

而这不可能通过a生成。

4、当a={{1, 1/2}, {-1, 1/2}}，行列式等于1，这个a也未必能够生成一个循环群：

MatrixForm[#] & /@ (Table[MatrixPower[a, n], {n, 1, 20}] // Union)

5、MatrixPower[a, 5]是由a生成的。

6、MatrixPower[a, 5] 的逆元素基本不可能用a生成：

MatrixPower[a, 5] // Inverse

7、看一下，能不能找到逆元素。

MatrixForm[#] & /@ (Table[MatrixPower[a, n], {n, 1, 100}] // Union)

1、给出一个三阶矩阵：

a = {{1, 1, 1}, {-1, 1, 0}, {0, -1, 0}}

2、MatrixPower[a, 2]

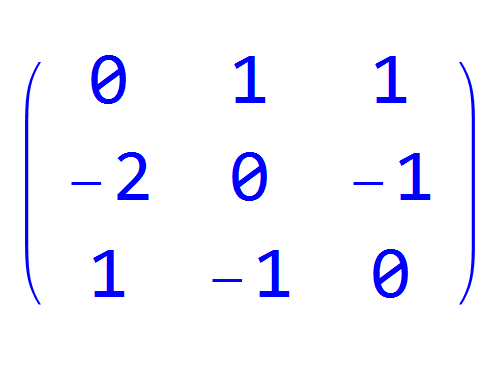
3、MatrixPower[a, 6]

这是一个单位矩阵，说明a可以生成一个6阶循环群。

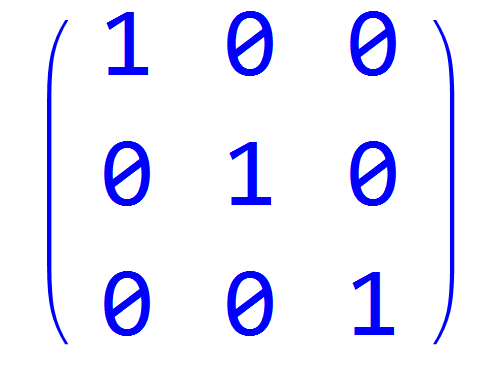
4、这个循环群的元素包括：

MatrixForm[#] & /@ (Table[MatrixPower[a, n], {n, 1, 20}] // Union)

5、验证可知，a的逆矩阵也在里面。

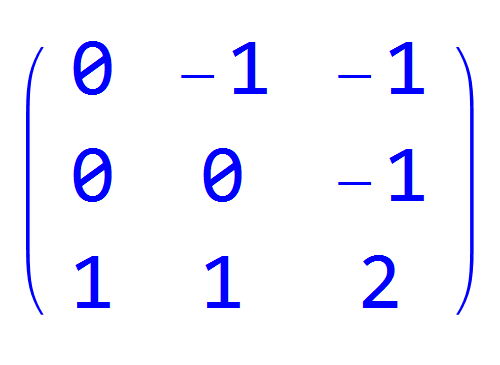
6、MatrixPower[a, 3]的逆矩阵是它自身：