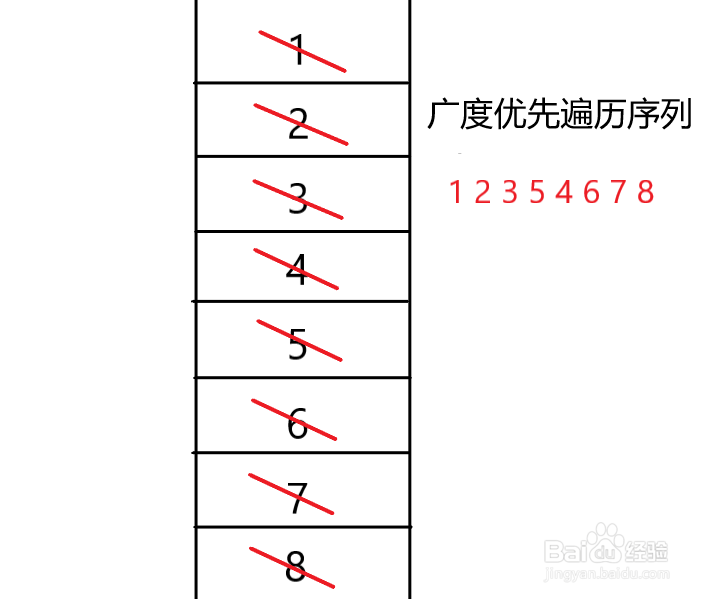
图的遍历方法

1、图的遍历是从某顶点出发访问图中每个节点，且每个节点仅访问一次。下图是我们今天要讲的图。接下来我们一起来学习吧。

1、深度优先遍历是指从图中某个节点出发，首先访问出发点，然后在出发点的邻接点中寻找一个未被访问过的节点，以该节点为新的出发点继续进行深度优先遍历。以下图为例，假设访问的第一个节点是1。

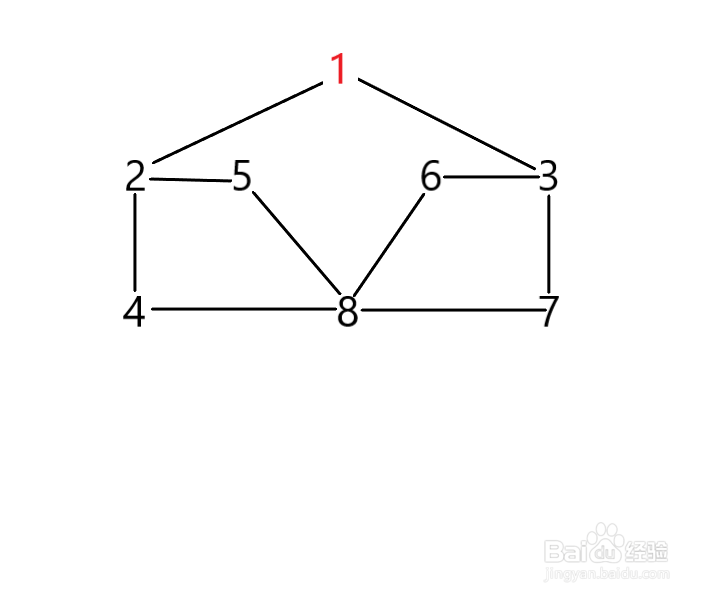
2、那么节点1的邻接点有2和3，并且2和3都没有被访问过。我们这里选择2，当然选择3也是可以的。

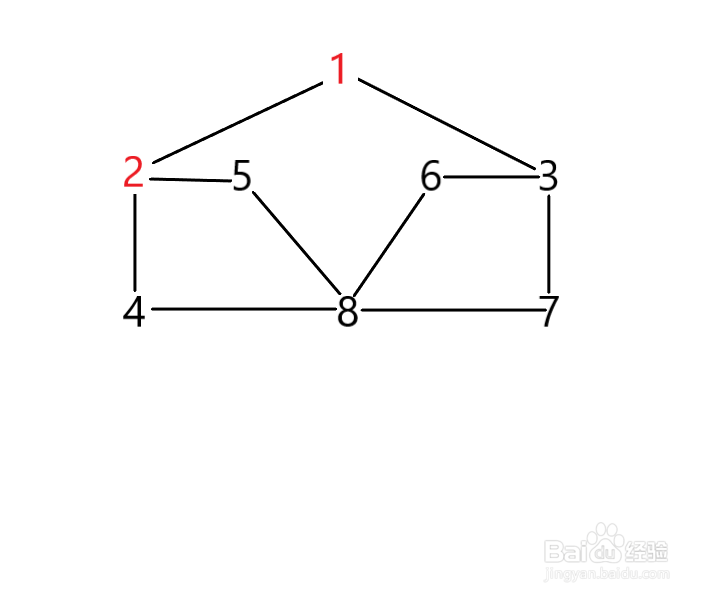
3、以2为新的出发点，2的邻接点有4和5，4和5都没有被访问过，那么我们这里选择4。

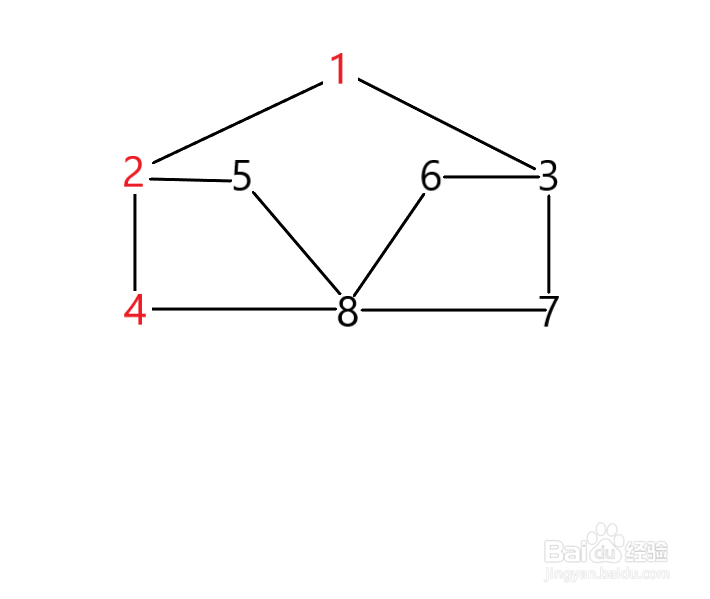
4、以4为新出发点，4的邻接点有2和8，其中2已经被访问过了，那么我们现在只能选择8。

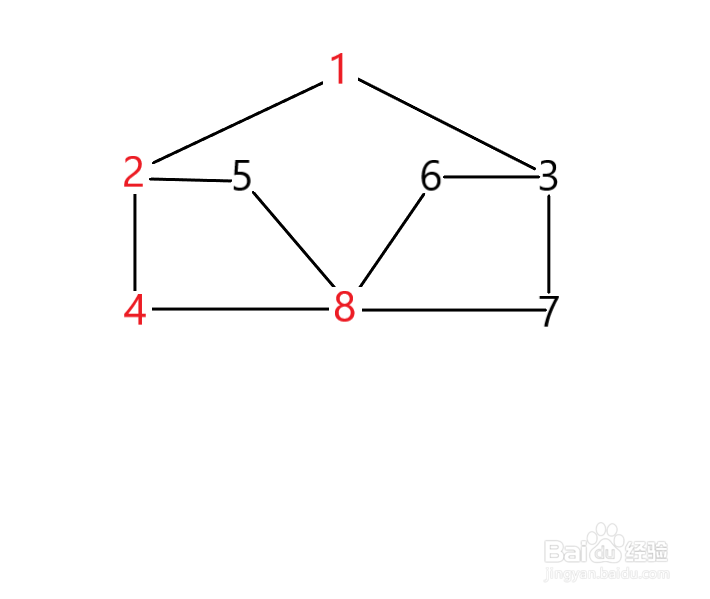
5、以8为新出发点，8的邻接点有4,5,6,7.其中5,6,7没有被访问我们选择5。

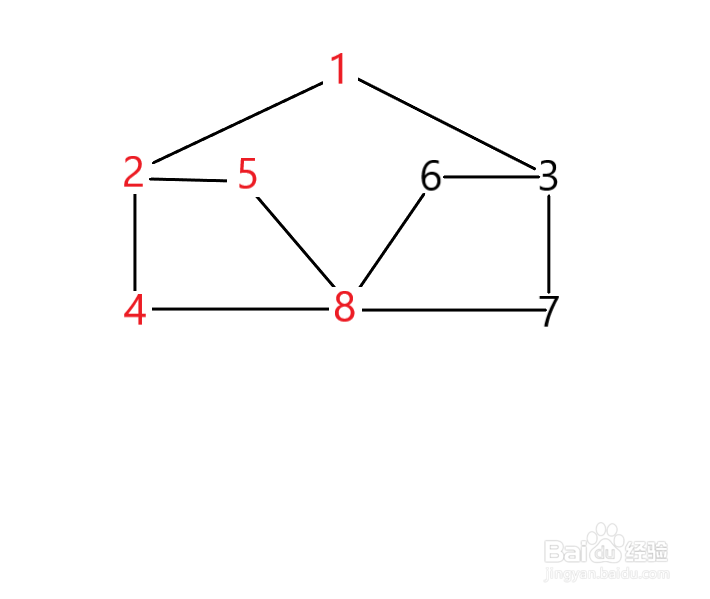
6、以5为新的出发点，5的邻接点有2和8，可是2和8都被访问过了，这时我们应该返回当前出发点的上一个出发点8，以上一个出发点8为新的出发点，继续寻找新出发点的未被访问过的邻接点。

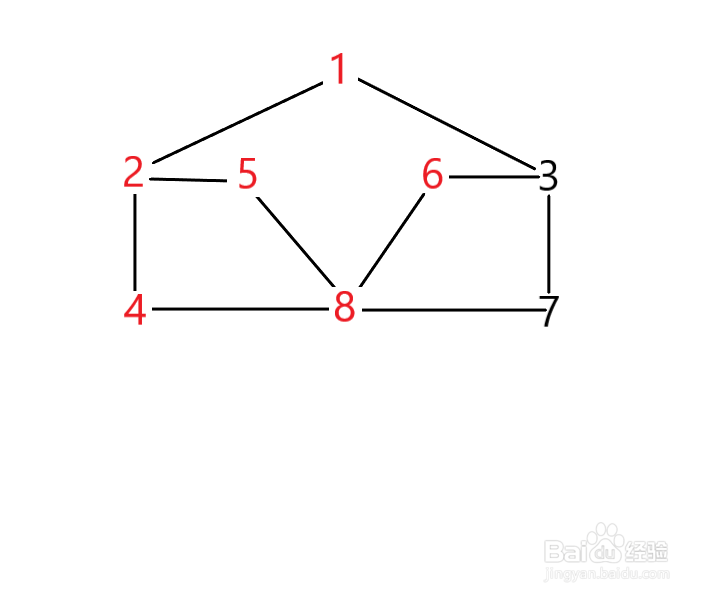
7、之后的节点的遍历逻辑是一样的，遍历完成后，我们将访问过的节点按顺序输出。即可得到我们的深度优先遍历序列。如果大家模拟正确的话，可能是如下图所示的序列，为什么这里说可能呢？因为其实我们的深度优先遍历序列是不唯一的。

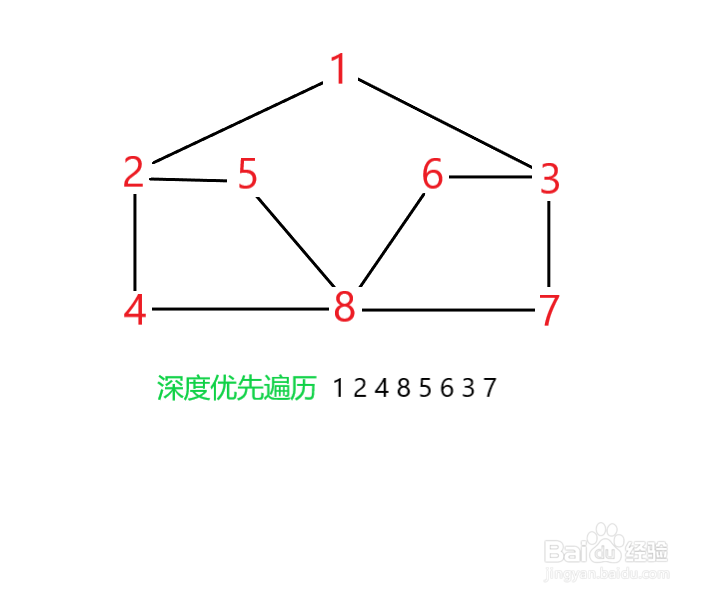
1、广度优先遍历是指从图中某一个节点出发，首先访问出发点，之后依次访问出发点的各个未被访问过的邻接点。然后分别从这些邻接点出发依次访问它们的邻接点。这里我们要注意，应使先被访问的出发点的邻接点先于后被访问的出发点的邻接点被访问，直至图中所有已被访问过的节点的邻接点都被访问到。

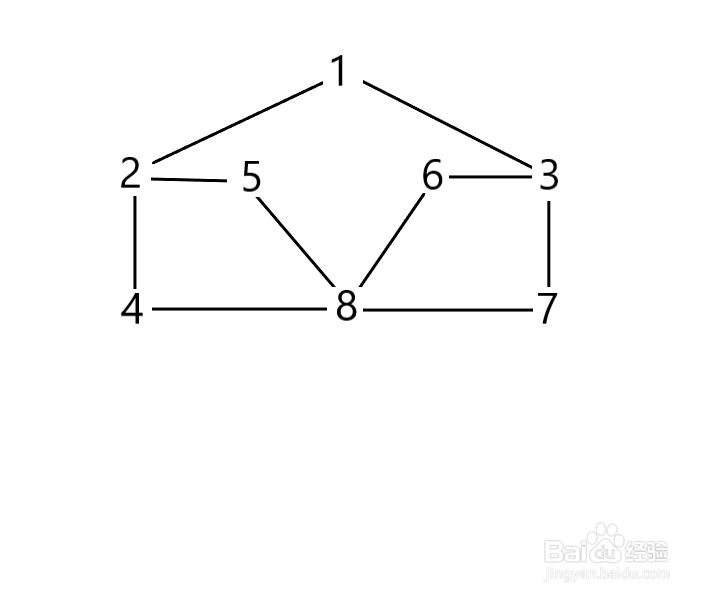
2、那这里我们要引入一个方法，就是创建一个队列，将节点和它的邻接点一次存入队列。这里我们首先选择节点1，那么这里的节点1的邻接点有2,3。如下图所示。

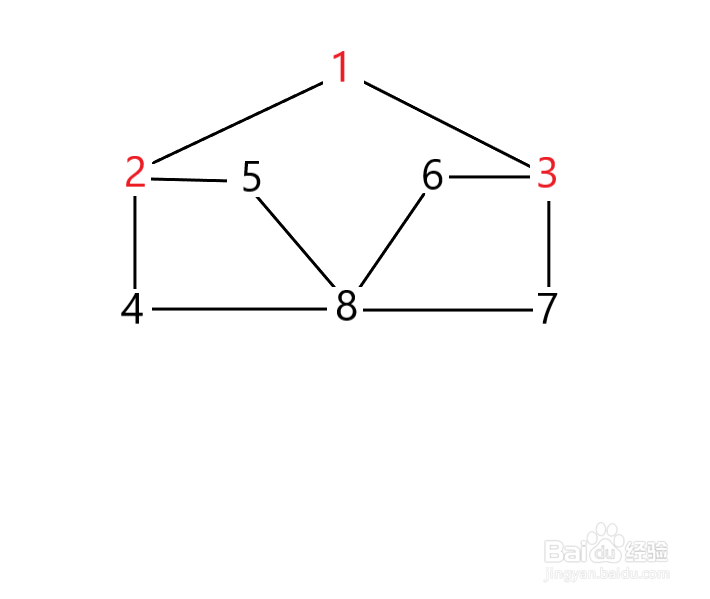
3、接下来我们把1存入队列，此时队列中只有一个节点1，当我们将节点1拿出队列时，我们将节点1的所有未被访问过的邻接点依次放入队列。如下图所示。

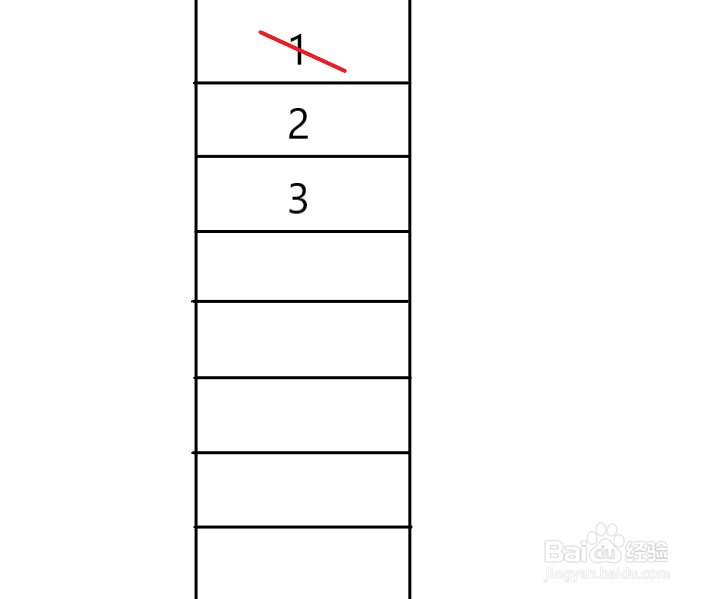
4、队列的特点是先进先出，那么我们先放入的是节点2，这时先出的也应当是节点2。当我们移出节点2时，也要把2的所有未被访问过的邻接点全部放入队列中。节点2的未被访问过的邻接点有4,5。

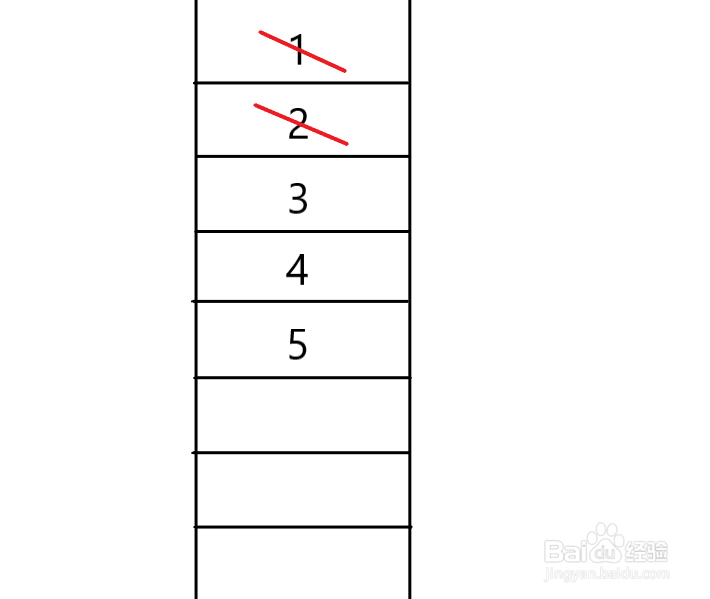
5、之后的节点的遍历逻辑相同，其实我们也可以发现广度优先遍历序列也不是唯一的。在这里放一个我练习的序列。