【Mathematica】科学计算向量夹角

1、如果给出两个具体向量，Mathematica可以直接算出夹角：

a = {1, 0}; b = -a; p = {1/2, 2};

VectorAngle[p - a, p - b]

2、但如果给定的向量里面有未知数，情况就不一样了：

a = {1, 0}; b = -a; p = {x, y};

VectorAngle[p - a, p - b]

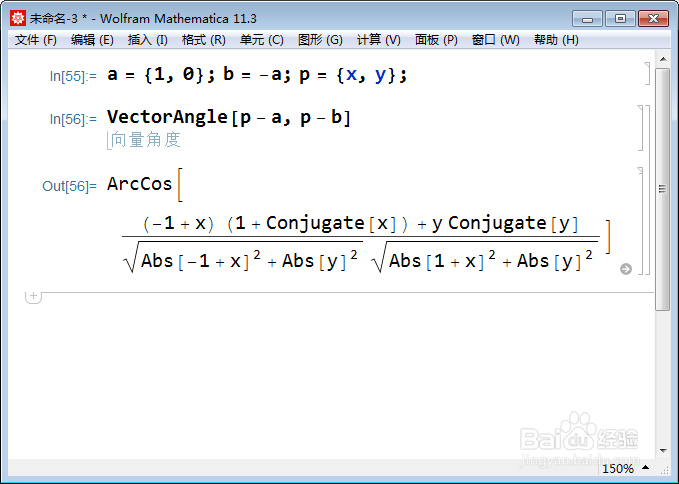
3、Mathematica默认x和y是复数。

如果需要，请把x和y限定为实数：Element[{x,y}, Reals]

具体代码如下：

Refine[VectorAngle[p - a, p - b],Element[{x, y}, Reals] ]

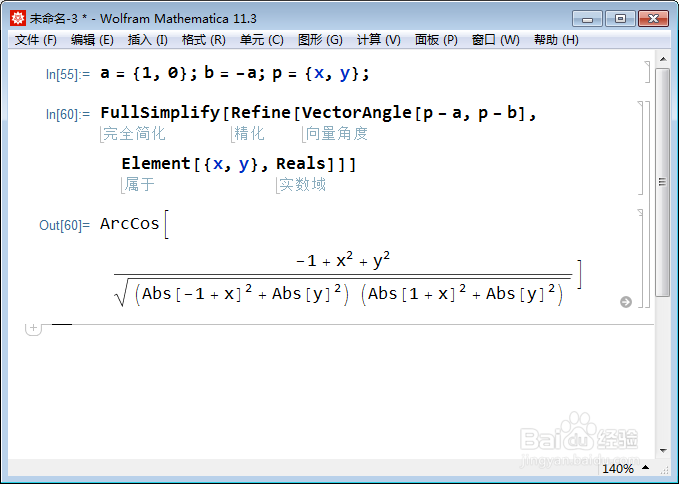
4、在外面化简：

FullSimplify[Refine[VectorAngle[p - a, p - b], Element[{x, y}, Reals]]]

化简效果不好。

5、在里面化简，也不够彻底：

Refine[FullSimplify[VectorAngle[p - a, p - b]], Element[{x, y}, Reals]]

6、增加一个限制条件：

Refine[FullSimplify[VectorAngle[p - a, p - b]], 

 Element[{x, y}, Reals] && -1 < x < 1]

脱去与x相关的绝对值符号。

7、再脱去与y相关的绝对值符号：

Refine[FullSimplify[VectorAngle[p - a, p - b]], 

 Element[{x, y}, Reals] && -1 < x < 1 && y > 0]

1、用Mathematica来解决一个具体的几何问题，题目内容如下图：

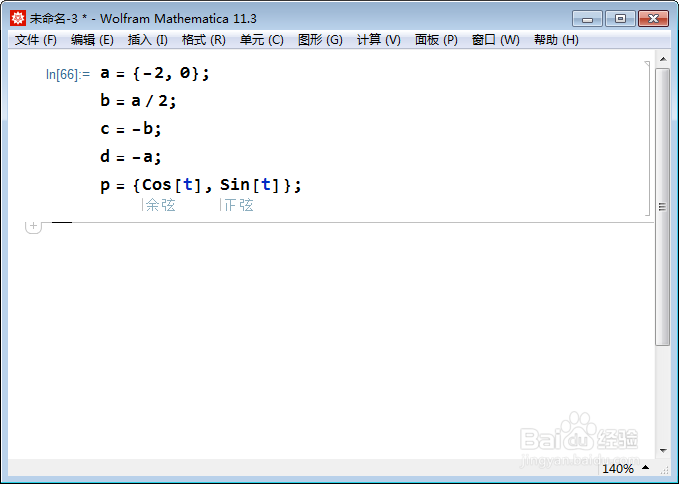
2、设定定点坐标：

a = {-2, 0}; b = a/2; c = -b; d = -a; p = {Cos[t], Sin[t]};

点p被限定在单位圆上。

3、α的正切值等于：

α = Tan[VectorAngle[p - a, p - b]] // FullSimplify

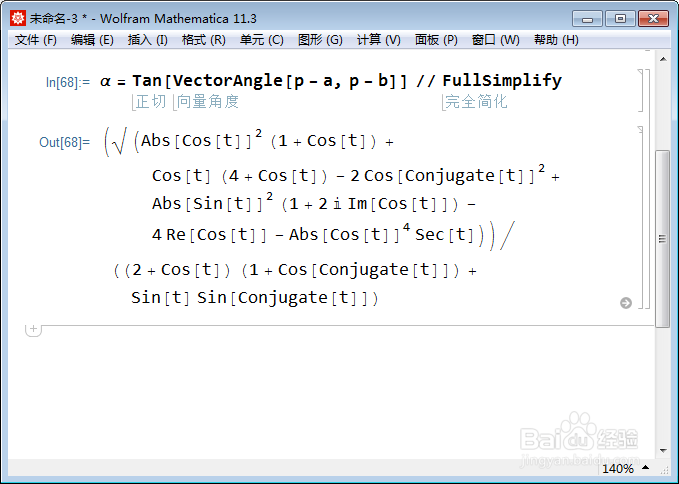
4、β的正切值等于：

β=Tan[VectorAngle[p - c, p - d]] // FullSimplify

化简最终结果：

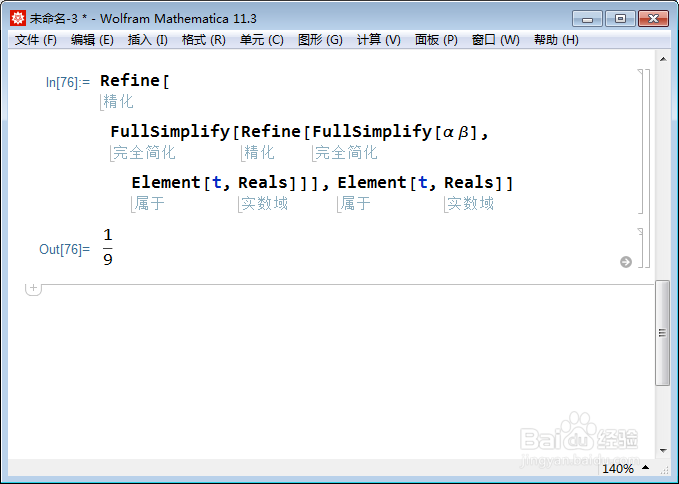
Refine[FullSimplify[α β], Element[t, Reals]]

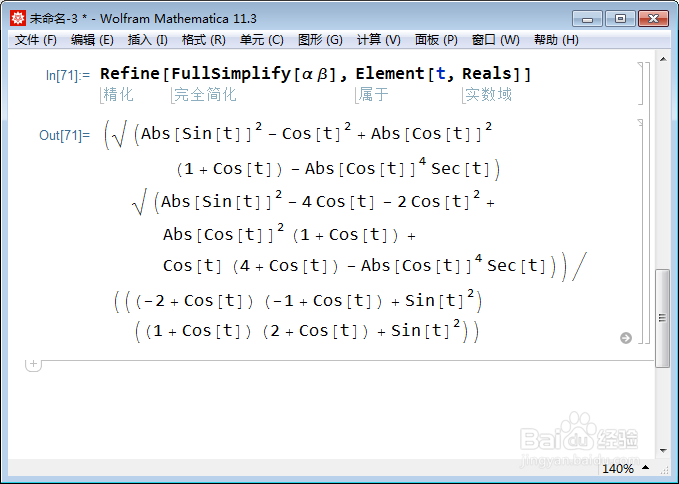
5、上面化简结果不理想，那就再化简一次：

Refine[FullSimplify[

  Refine[FullSimplify[\[Alpha] \[Beta]], Element[t, Reals]]], 

 Element[t, Reals]]

好了，原题答案就是1/9。