用Mathematica绘制球面曲线
1、 先画球面,这里以单位球面为例,可以有三种画法:
ParametricPlot3D[{Sin[u] Cos[v], Sin[u] Sin[v], Cos[u]}, {u, 0,2 Pi}, {v, 0, Pi}]
SphericalPlot3D[1, {x, 0, Pi}, {y, 0, 2 Pi}]
ContourPlot3D[x^2 + y^2 + z^2 == 1, {x, -1.1, 1.1}, {y, -1.1, 1.1}, {z, -1.1, 1.1}]
可以看到,三种方法画出的单位球面的网格线有明显的不同。



2、 绘制球面和柱面交在一起的情形,其中,柱面的直径长度是球随随冷的半径长度,柱面的一条母线过球心。
其中,为了方便计算,把球半径设为2。
球面的方程是:
x^2 + y^2 + z^2 == 2^2, {x, -2.1, 2.1}, {y, -2.1, 2.1}, {z, -2.1, 2.1}
柱面的方程是:
(x - 1)^2 + y^2 == 1, {x, -2.1, 2.1}, {y, -2.1, 2.1}, {z, -2.1, 2.1}

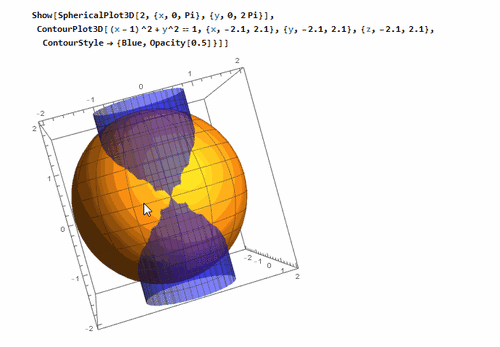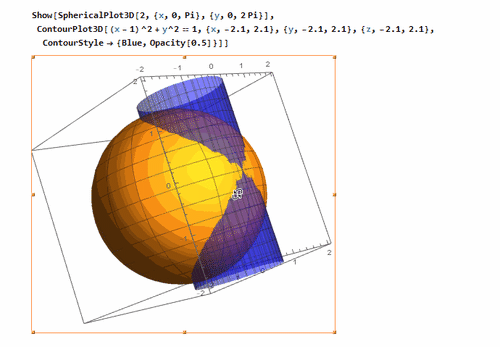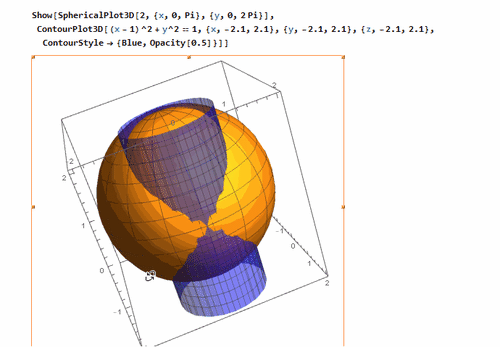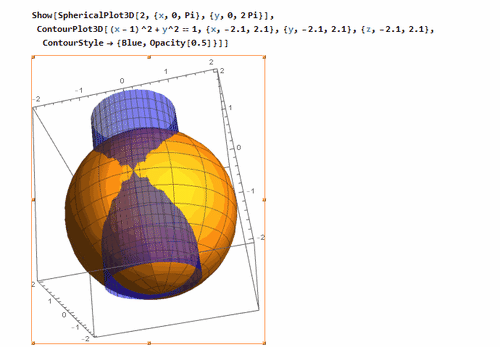

3、 再来绘制著名的Viviani Curve——音译为“维维亚尼”曲线。
在网上找英吩到一个例子,照葫芦画瓢。
结果感觉很不满意!

4、 在Mathematica智囊团里面,群友告诉我,原因是图片精度不够裕番的缘故,并提供了以下代码。结果很好!
我在这里表示感谢!

5、 网友还给出一个更简洁的代码,用BoundaryStyle来画两个曲面的相交线,用Tube把相交线画成“管状”。

1、 现在来绘制一个球面螺旋线,它的一个参数方程是:
{Sin[Pi t] Cos[36 Pi t], Sin[Pi t] Sin[36 Pi t], Cos[Pi t]};
当自变量的取值范围是0到2π的时候,出来的图形是双层的螺旋线:
ParametricPlot3D[{Sin[Pi t] Cos[36 Pi t],Sin[Pi t] Sin[36 Pi t],
Cos[Pi t]}, {t, 0, 2 Pi}, PlotStyle -> {Green, Thickness[0.005]}]

2、 怎么把第二层去掉呢?自然是缩小自变量的最大值。大体试验了一下,最大值应该小于(7.6π/24):
ParametricPlot3D[{Sin[Pi t] Cos[36 Pi t], Sin[Pi t] Sin[36 Pi t],
Cos[Pi t]}, {t, 0, 7.6 Pi/24}, PlotStyle -> {Blue, Thickness[0.005]}]

3、 感觉太密集了是不是?那么,我们用一个互动代码:
Manipulate[
ParametricPlot3D[{Sin[Pi t] Cos[b Pi t], Sin[Pi t] Sin[b Pi t],
Cos[Pi t]}, {t, 0, 2 Pi},
PlotStyle -> {Green, Thickness[0.01]}], {b, 1, 36, 1}]
其中,参数b决定着球面螺旋的圈数。
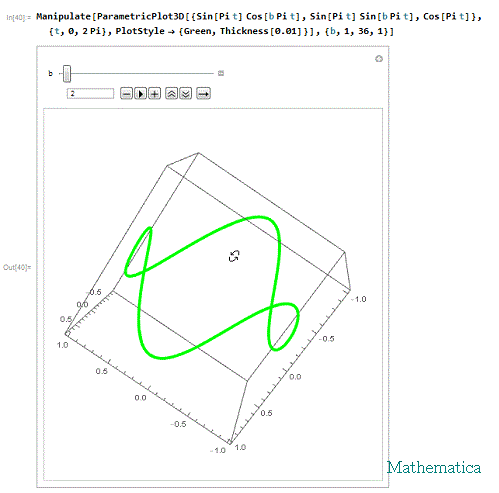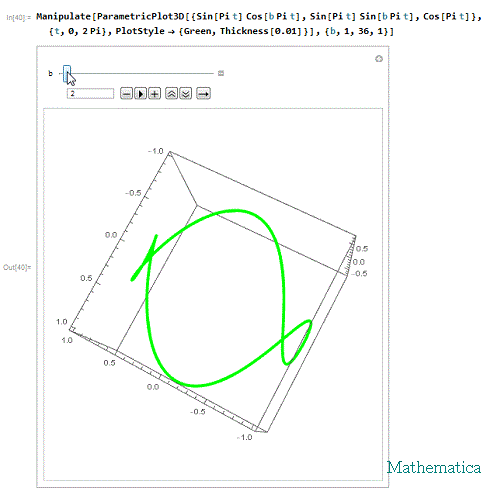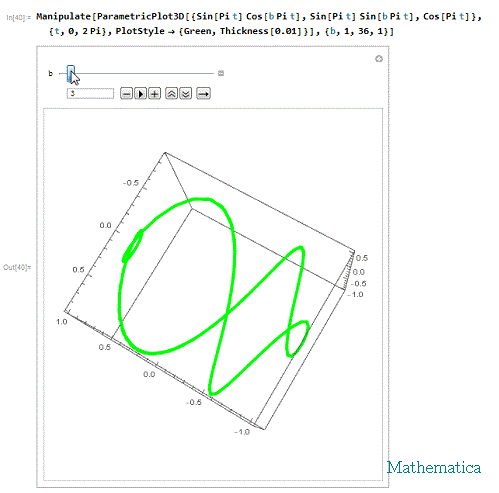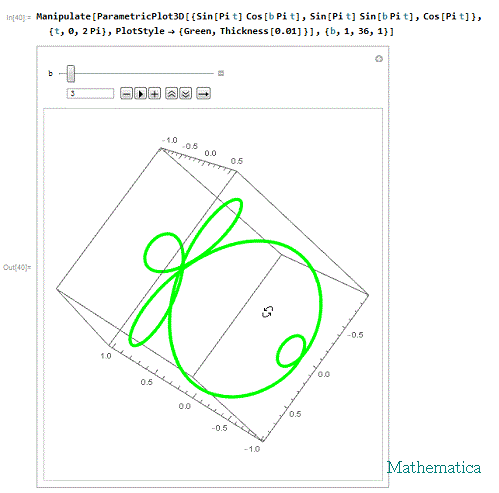
4、 我们可以发现,当b=1时,出来的曲线恰好就是维维亚尼曲线。所以,维维亚尼曲线也是一种球面螺旋。

5、 这里,再给出另一个球面螺旋的参数方程——这是无影东瓜给出的—:
{Sqrt[1 - z^2] Cos[k z], Sqrt[1 - z^2] Sin[k z], z}
其中,k决定了螺旋线的圈数,而且,这个螺旋线是一层的!
With[{k = 36},
ParametricPlot3D[{Sqrt[1 - z^2] Cos[k z], Sqrt[1 - z^2] Sin[k z],
z}, {z, -1, 1}, PlotStyle -> {Lighter@Blue, Thickness[0.01]}]]

1、 先来一个特殊的、不知道名字的曲面——x^y + y^z + z^x == 2。
画图代码是:
ContourPlot3D[x^y + y^z + z^x == 2, {x, 0, 1}, {y, 0, 1}, {z, 0, 1},
ContourStyle --> {Opacity[0.8]}]
运行结果比较难看!

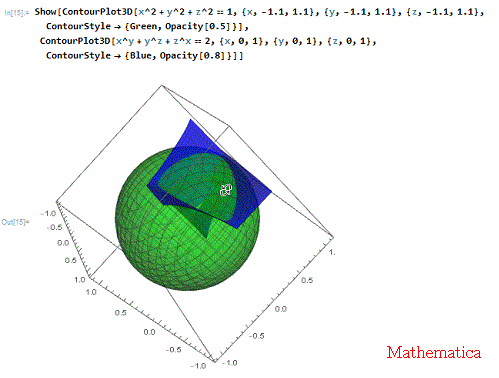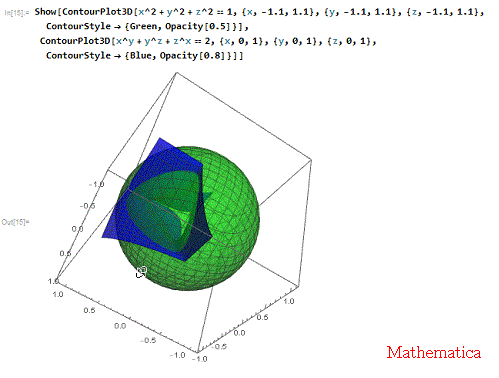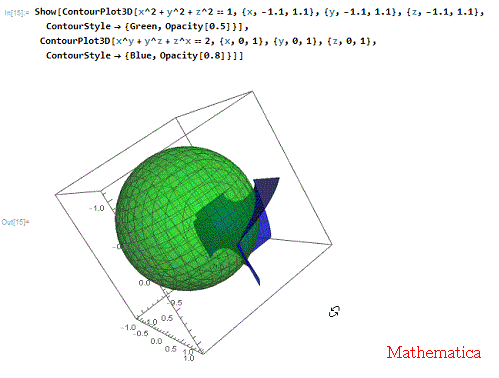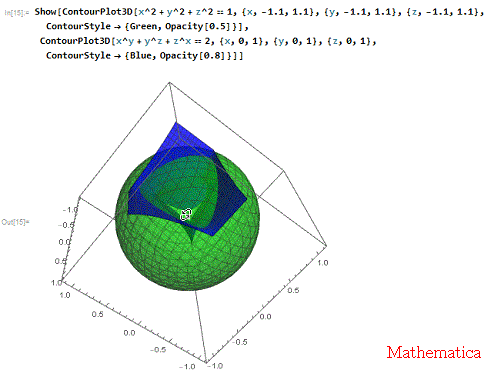
2、 所以,用单位球面把它的底部给包起来!
Show[ContourPlot3D[
x^2 + y^2 + z^2 == 1, {x, -1.1, 1.1}, {y, -1.1, 1.1}, {z, -1.1,
1.1}, ContourStyle -> {Green, Opacity[0.5]}],
ContourPlot3D[x^y + y^z + z^x == 2, {x, 0, 1}, {y, 0, 1}, {z, 0, 1},
ContourStyle -> {Blue, Opacity[0.8]}]]
这里,给球面一个半透明效果!
3、 我们感兴趣的是,画出这两个曲面的交线。从网上找了很多方法,都无果!
好在,Mathematica智囊团里面的“胡呵呵呵”给出了一个好的方法:
Show[SliceContourPlot3D[x^y + y^z + z^x - 2,
x^2 + y^2 + z^2 == 1, {x, 0, 1}, {y, 0, 1}, {z, 0, 1},
Contours -> 0, ContourStyle -> {Red, Thickness[0.01]}],
ContourPlot3D[x^y + y^z + z^x == 2, {x, 0, 1}, {y, 0, 1}, {z, 0, 1},
ContourStyle -> {Green, Opacity[0.8]}]]
遗憾的是,没有能够求出交线的参数方程。因此,这条曲线不能用作ViewPoint——观察点的移动路径!
