大数据SPSS分析总结

1、1.解决问题

（1）对抽取的样本按照某个类别时行分别计算相应常见统计量，如平均数，标准差；

（2）检验两个相关的样本是否来自具有相同均值的总体；

（3）两个有联系的正态总体均值是否显著差异。

2、2.如何选择

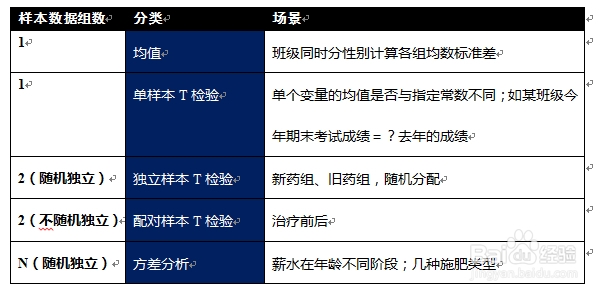
3、3.方差分析

3.1条件：

（1）总体必须满足正态分布（QQ图，K-S检验进行验证）；

（2）观测变量各总体的方差应该相同；(齐次性检验>0.05)

（3）控制变量一定是取值有限的名义尺度、顺序尺度变量。

3.2分类：（根据控制变量的个数）

单因素方差分析、多因素方差（薪水－年龄和工作年限）；

协方差分析：扣除协变量影响（年龄和工作年限相关，扣除工作年限影响）

1、1.何时用呢？

在无法获得有关总体分布的相关信息时――

通过样本检验关于总体的相关假设的检验方法

2、2.如何选择呢？

1、这不难理解，在此不多解释，重点说一下其分类，知道如何选择就好了。

1、1.总体看各回归方法

2、2.下面对重点环节进行阐述

一元线性回归步骤：

（1）作两变量散点图－观相关性

（2）选定自/因变量，进行回归分析

（3）回归方程检验（方程意义、显著性、系数显著性、残差（观测值-预测值）分析）

（4）回归方程修正

3、3.多元线性回归：为了弥补一元线性回归无法完全解释因变量变化信息而引入（只有当一元回归效果很差才考虑，且自变量间互不相关）

步骤：选择因变量－确定自变量对因变量的解释力－消除自变量多重关性（回归）－拟合线性回归方程（多元线性回归）－方程检验－残差分析－模型确认并用于预测

4、4.多元――多重共线（自变量间有较强的相关性）

如何发现：观察自变量间相关分析；回归分析中多重共线诊断

解决方法：采用回归让SPSS自动选择合适自变量，用于建立回归方程（剔除已选变量发生多重花线的）

5、5.曲线回归：散点图中发现－可能是弱非线性－曲线回归

难点：曲线形式的选取；不确定只好选取多种可能合适的模型－SPSS计算参数－根据判定系数（可决系数）－选择最优模型

1、1.适用场景：调查问卷往往需要被访者对一个问题，多个选项进行选择

SPSS处理：将一个多选项问题分解成若干个单选问题，对应每个单选问题设置一个变量。

2、2.如何选择

1、1.步骤

2、2. 相似性指标

3、3.聚类分析

适用：可以在没有先验分类的情况下，通过观察对数据进行分类

目标：使组内数据对象具有很高相似度，而组间具有较大的差异性

4、4.判别分析

1、1.因子分析

是一种数据简化的技术，通过研究众多变量之间的内部依赖关系，探求观测数据中的基本结构，并用少数几个假想变量来表示其基本的数据结构。

即：假想变量   反映  主要信息  是不可观测的潜在变量  即  因子

（1）主要思路：降维    简化数据结构

（2）目的：将（具有错综复杂关系的）变量  综合为  （数量较少的）  因子

以再现   原始变量与因子的关系，  通过不同的因子，对变量进行分类

消除     相关性，在信息损失最小的情况下，降维

2、2.步骤

选取因子分析的变量（选相关性较大的，利于降维）――标准化处理；

根据样本、估计随机向量的协方差矩阵或相关矩阵；

选择一种方法――估计因子载荷阵，计算关键统计特征；

进行因子旋转，使因子含义清晰化，并命名，利用因子解释变量的构成；

计算每个因子在各样本上的得分，得出新的因子得分变量――进一步分析。

3、3.如何分析

检验变量间偏相关度KMO值>0.6,才适合做因子分析；

调整因子个数，显示共同特征后即可命名。

4、4.分类

5、5.对应分析基本理论