证明群G的子集H是G的子群,当且仅当 h≠Φ,a,b∈H→a(b^-1)∈H
必要性:若H是G的子群,自然非空,并对乘法和取逆封闭,从而H≠∅,并对任意a,b∈H,有ab⁻¹∈H。
充分性:首先,由H≠,可取a∈H,由条件得e=aa∈H,因此H包含G的单位元e。
子集是一个数学概念:如果集合A的任意一个元素都是集合B的元素,那么集合A称为集合B的子集。符号语言:若∀a∈A,均有a∈B,则A⊆B。
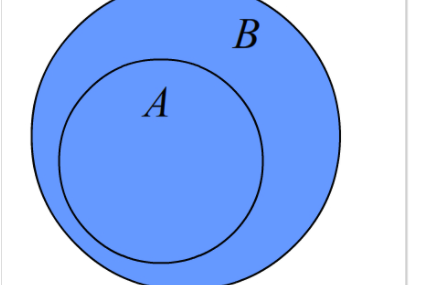
真子集
如果集合A是B的子集,且A≠B,即B中至少有一个元素不属于A,那么A就是B的真子集,可记作:A⊊B。
符号语言:若∀a∈A,均有a∈B,且x∈B使x∉A,则A⊊B。集合A就是集合B的真子集。
声明:本网站引用、摘录或转载内容仅供网站访问者交流或参考,不代表本站立场,如存在版权或非法内容,请联系站长删除,联系邮箱:site.kefu@qq.com。
阅读量:187
阅读量:143
阅读量:170
阅读量:125
阅读量:147