6阶群的分类、生成元、子群和Cayley图

1、6阶循环群只有一个生成元。

2、对应的Cayley图如下（矩阵表示）。

3、6阶循环群的子群：

1阶子群、2阶子群、3阶子群、6阶子群各一个。

1、3阶对称群有两个生成元。

2、矩阵表示的Cayley图。

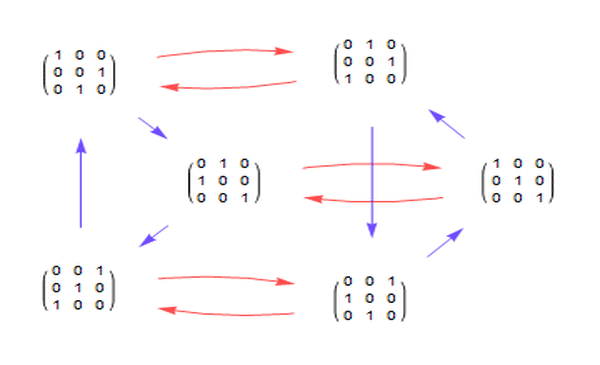
3、子群包含1个1阶子群、2个3阶子群、1个3阶子群、1个6阶子群。

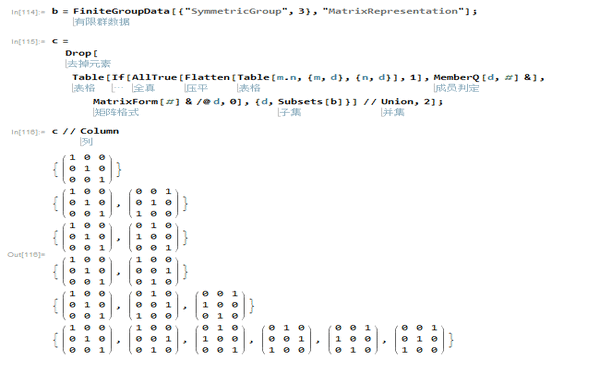
1、Mathematica画出的3*2的Abel群的Cayley图竟然是错的，狂晕！

.

.CayleyGraph[AbelianGroup[{3, 2}]]

.

这一点真是很奇怪，Mathematica居然也会坑人了。

2、3*2的Abel群的子群，有1阶子群、2阶子群、3阶子群、6阶子群各一个。

实际上，3*2的Abel群同构于6阶循环群。

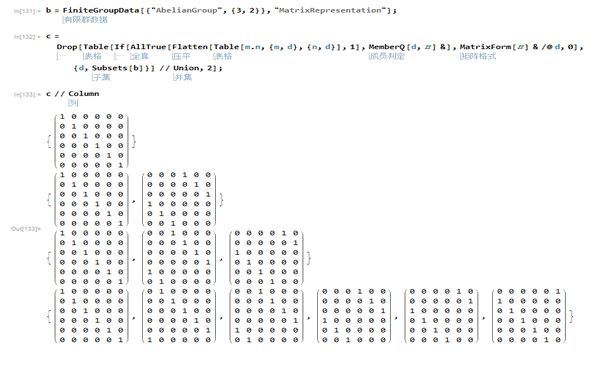
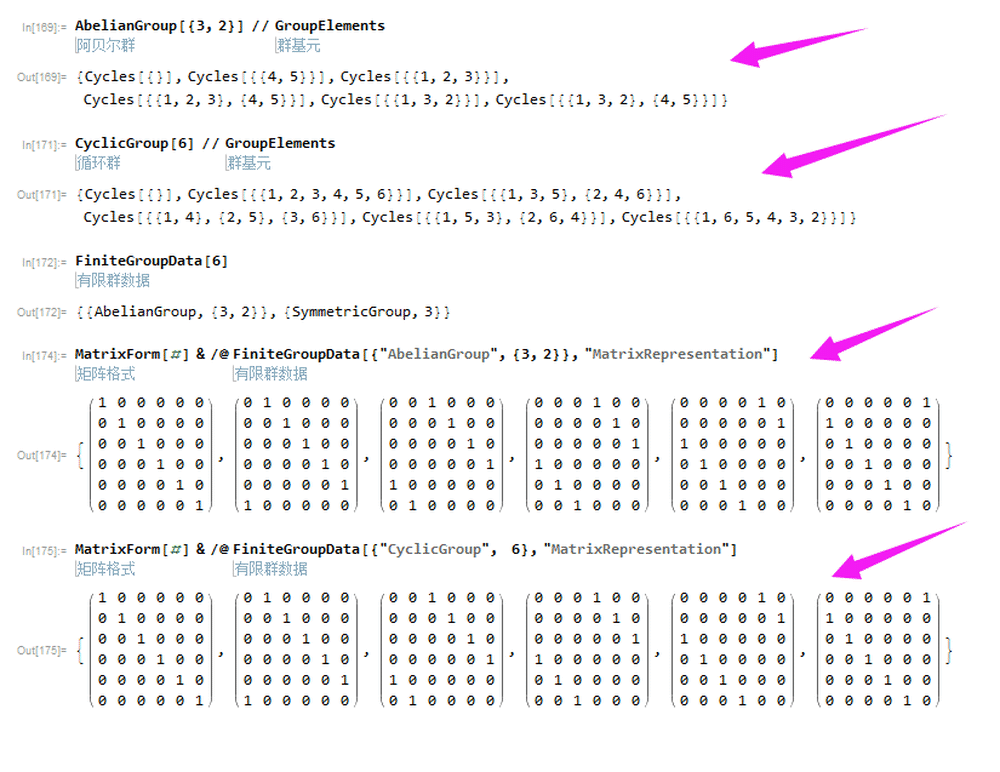
3、6阶循环群、3*2的Abel群的置换表示不一样，但是它们的矩阵表示却完全一致。

这是否能够说明，群的矩阵表示更接近本质呢？