两个向量正交怎么算

1、给出两个向量：

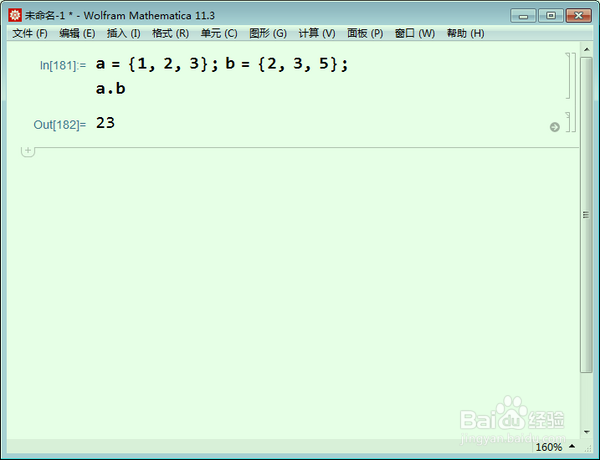
a = {1, 2, 3}; b = {2, 3, 5};

要判断这两个向量是否正交，用点乘来验证：

a.b

如果运行结果不等于0，表示二者不垂直，也就不是正交关系。

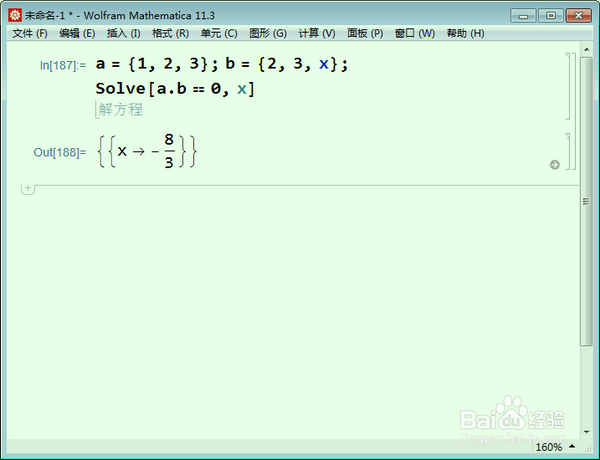
2、a = {1, 2, 3}; b = {2, 3, x};

如果a和b正交，x应该等于多少？

Solve[a.b == 0, x]

解得点b是一个孤立点，是零维空间。

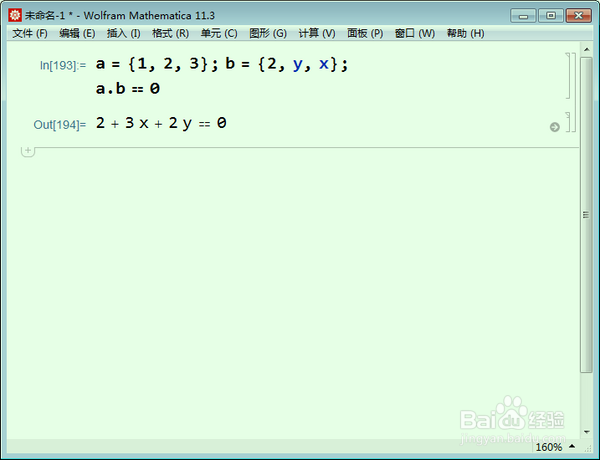
3、a = {1, 2, 3}; b = {2, y, x};

此时，a和b正交，那么b是一暗拒条直线上的点。

a.b == 0

这是一维空间。

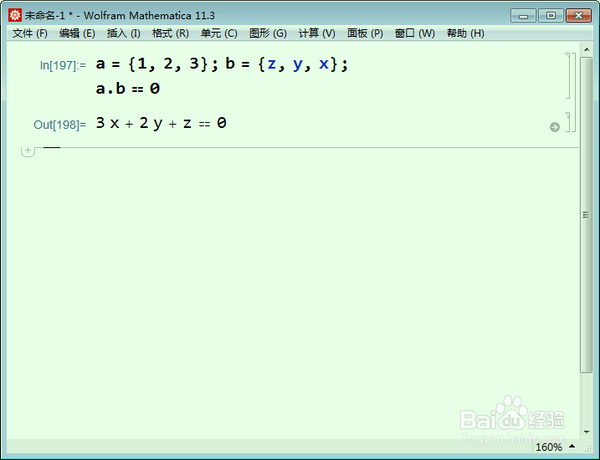
4、a = {1, 2, 3}; b = {z, y, x};

此时a和b正交，b在一个平面上：

a.b == 0

这是二维空间。

三维空间里面，没可能撑起泛何互另一个三维空间。

5、在曲线论里面，参数方程曲线的切向量，可以视为参数方程的导数。

但切向量的导数却不一定是曲线的法向量：

r = {Cos[2 t], Sin[3 t]};

D[r, t].D[r, {t, 2}]不恒等于0。

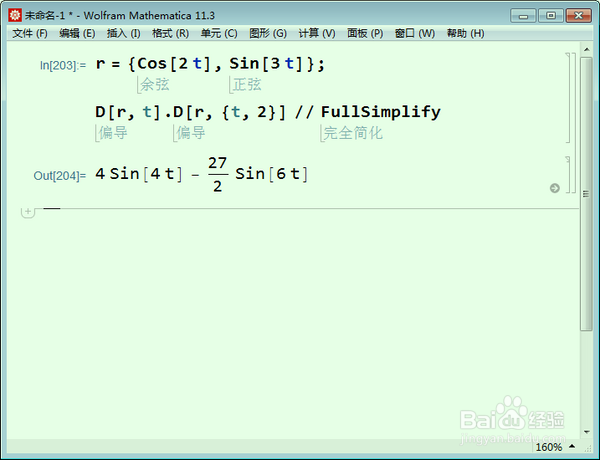
6、实际上，曲线法向耻处量是曲线单位切向量的导数：

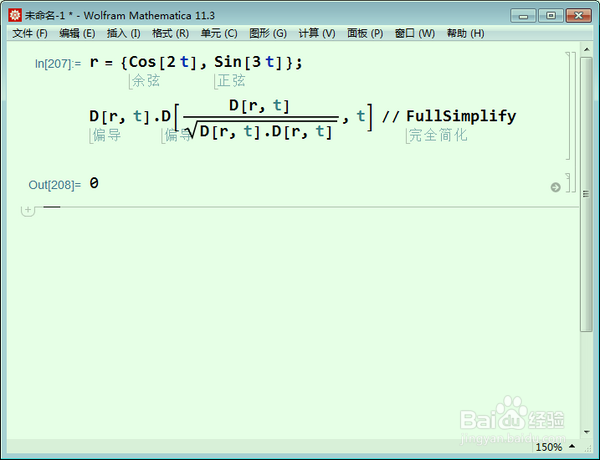
D[r, t].D[D[r, t]/Sqrt[D[r, t].D[r, t]], t] // FullSimplify

答案是0。

注意，前提是，这个曲线的参数方程可以求导。