用matlab求解方程非线性规划问题

1、开始第一步我们打开在电脑桌面找到matlab小程序，然后鼠标右击打开桌面上matlab程序，运行起来。由于不同人电脑的配置不一样，软件打开的速度也有所不同，一般固态硬盘比机械硬盘运行的要快好多。大家稍微等待一下。

2、我们为了便于保存数据，我们点击matlab左上角新建脚本命令，创建新的脚本，创建M文件，也便于程序的保存，我们可以将其保存在电脑的其他盘，以便于我们的寻找和使用，这也是比较常见的方式。

3、这是一个常见的二次非线性规划的方程，有目标函数，有约束条件，让其在约束条件的情况下求其的最优解和最优值

下面问题有五个约束条件

求约束条件的最小值

4、首先建立一个M文件fun_ex5.m文件

输入程序如下

 function f=fun_ex5(x);

 f=2*x(1)-x(2)*exp(x(1));

 其中exp代表指数函数

*代表乘

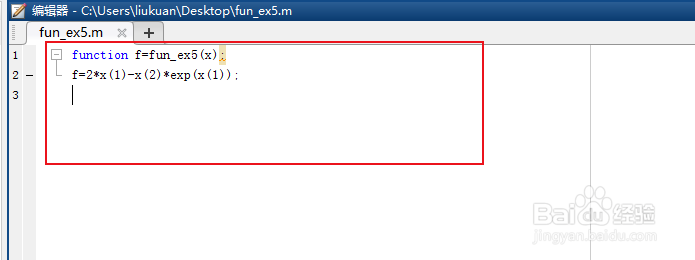
5、新建的文件如下图所示

是一个m文件

m文件只能通过matlab打开

不能再桌面上直接双击打开

大家注意下

6、建议另一个m文件，文件名为mycon_ex5.m，定义非线性的约束

程序如下

function [g,ceq]=mycon_ex5(x)

 g=[x(1)^2+(x2)^2-12;x(1)^2-x(2)^2-5];

 ceg=[ ];

注意符号书写的方式

以及字母书写方式

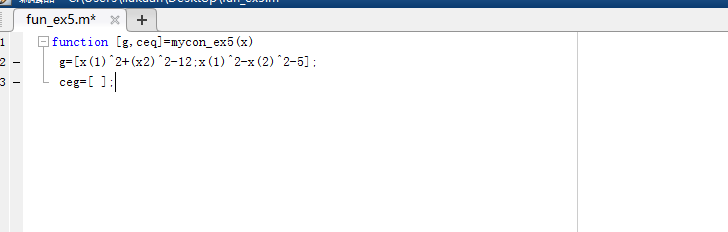
7、新建的文件如下图所示

是一个m文件

m文件只能通过matlab打开

不能再桌面上直接双击打开

大家注意下

8、输入程序：

>> x0=[1;1];

>> lb=[0;0];

>> ub=[5;8];

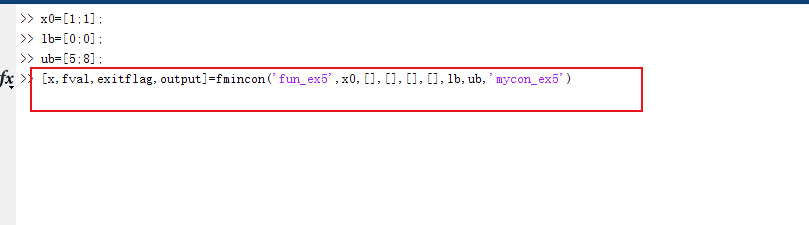
9、输入程序：

>> [x,fval,exitflag,output]=fmincon('fun_ex5',x0,[],[],[],[],lb,ub,'mycon_ex5')

记住字母书写的方式

以及输入状态

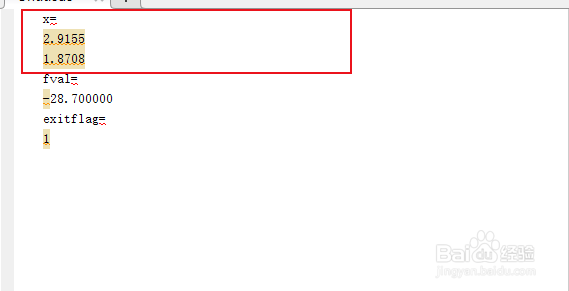
10、最优值为

fval=-28.7000

11、最优解为

x=2.9155

1.8708