三角函数y=2sin(2x+π/8)的单调凸凹等性质

1、三角函数y=2sin(2x+π/8)的定义域、值域、单调、周期、对称轴、切线等有关性质。

1、正弦函数y=2sin(2x+π/8)在极值处有对称轴，即：

2x+π/8=kπ+π/2,k∈Z.

2x=kπ+π/2-π/8

则对称轴为：x=(kπ/2)+3π/16.

2、函数的单调性也叫函数的增减性。当函数 f(x) 的自变量在其定义区间内增大(或减小)时，函数值f(x)也随着增大(或减小)，则称该函数为在该区间上具有单调性。

3、函数的单调性是函数的重要性质，反映了随着自变量的增加函数值的变化趋势。

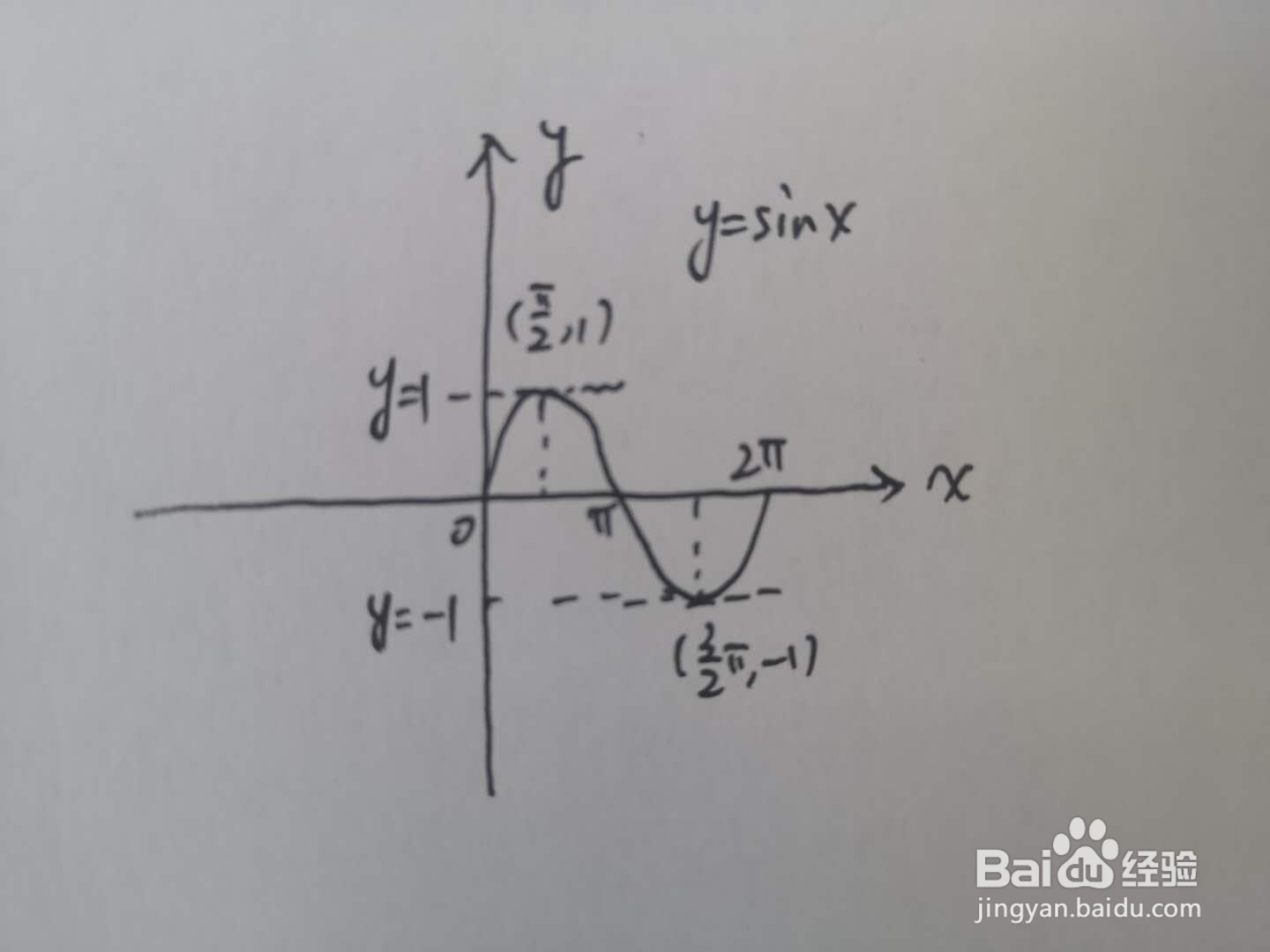
本例子主要介绍通过基本正弦函数y=sinx的单调性，去求解复合正弦函数y=2sin(2x+π/8)的单调性及单调区间。

1、求该三角函数y=2sin(2x+π/8)的一阶、二阶导数等。

先求出一阶导数为：y '=4cos(2x+π/8).，

再求二阶导数，即y''=d^2y/dx^2=-4sin(2x+π/8）*2=-sin(2x+π/8）。

可见正弦函数的多阶导数是在正弦和余弦函数之间互相转换。

2、求y=2sin(2x+π/8)图像上A((1/48)π，1)和B（(9/16)π，-√2）处的切线方程。

解：y=2sin(2x+π/8)，则：

y '=4cos(2x+π/8).

(1)在点A((1/48)π，1)处，有：

y '=4cos[2*(1/48)π+π/8]=4cosπ/6=4√3/2,

则该点处的切线方程为：

y-1=4√3/2[x-(1/48)π]。

3、求图像y=2sin(2x+π/8)半个周期内与x轴围成的面积。

解：先求其中半个周期内x的坐标点，即：

C(-(1/16)π,0,),D((3/16)π,0).

此时围成的区域面积为：

S=∫[Cx，Dx]ydx

=∫[Cx，Dx]2sin(2x+π/8)dx

=∫[Cx，Dx]sin(2x+π/8)d(2x+π/8)

=-cos(2x+π/8)[-(1/16)π,(3/16)π]

=-(cosπ/2-cos0)

=1.

4、求直线y=12x/π+(3/4)与正弦函数y=2sin(2x+π/8)围成区域的面积。

解：y1=12x/π+(3/4)与y2=2sin(2x+π/8)

的交点分别为：

E(-(1/8)π,0,),F((1/48)π，1).

5、可见定积分，是求解曲线与坐标轴、曲线与直线围成区域面积计算的重要方法。

1、对于任意一个实数x都对应着唯一的角，而这个角又对应着唯一确定的正弦值sin x，这样，对于任意一个实数x都有唯一确定的值sinx与它对应，按照这个对应法则所建立的函数，表示为f(x)=sinx，叫作正弦函数。

2、      正弦函数的几个数量等式关系：（1）平方和关系：:（sinα）^2 +（cosα）^2=1；（2）积的关系：sinα = tanα × cosα（即sinα / cosα = tanα ）；(3)倒数关系:sinα × cscα = 1;(4）商的关系：sinα / cosα = tanα = secα / cscα。

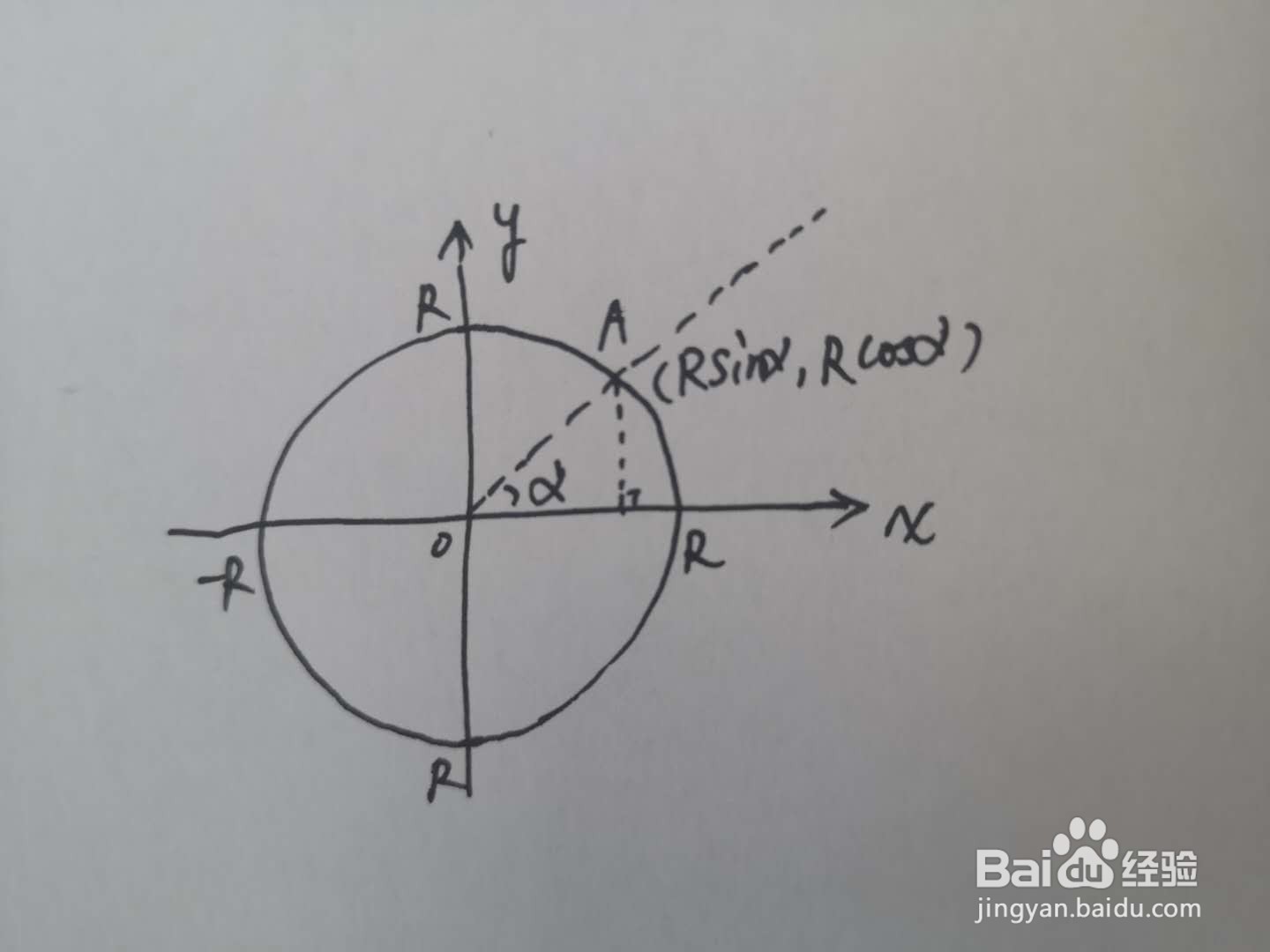
3、由于正弦的导数是余弦，余弦的导数是负的正弦，因此正弦函数满足微分方程y''=-y,这就是正弦的微分方程定义。