【Mathematica】分段函数的迭代

1、给出如下的分段函数：

g[x_]:=Piecewise[{{x^2,0<=x<=1},{1-(x-1)^2,1<x<=2}}]

其图像如下：

Plot[Nest[g,x,1],{x,0,2},AspectRatio->Automatic]

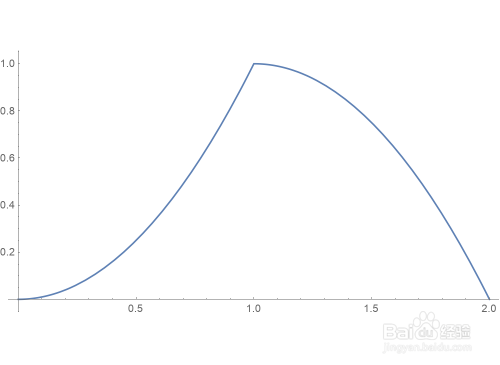
2、函数g的二次迭代是g[g[x]]：

Plot[Nest[g,x,2],{x,0,2},AspectRatio->Automatic]

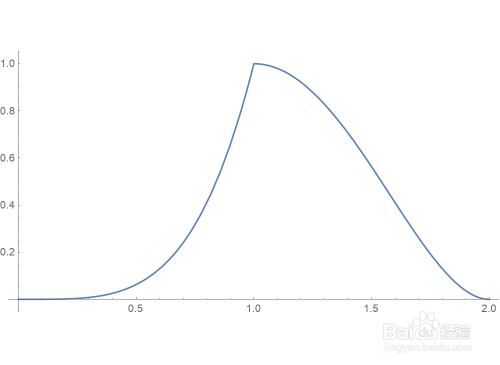
3、分段函数的迭代是复杂的：

Nest[g,x,2]

4、化简一下，或许会比较清楚：

Nest[g,x,2]//FullSimplify

5、这个函数有一个优点，那就是迭代结果仍旧是二段，且分段的位置不变：

Nest[g,x,5]//FullSimplify

其图像如下。

6、下面这个函数，就不这么容易处理了：

g[x_]:=2Piecewise[{{x^2,0<=x<=1},{1-(x-1)^2,1<x<=2}}]

7、g的二次迭代，在区间[1,2]里面有四个分段：

Nest[g,x,2]//FullSimplify

8、g的三次迭代，则是八个分段：

Plot[Nest[g,x,3],{x,0,2},AspectRatio->Automatic,PlotRange->All]