【微分几何】球面的参数方程和uv平面

1、如果u=v，那么就在uv平面上画出了一条直线（实际上只能是线段）。

ParametricPlot[{u, u}, {u, 0, 2 Pi}, PlotStyle -> Green]

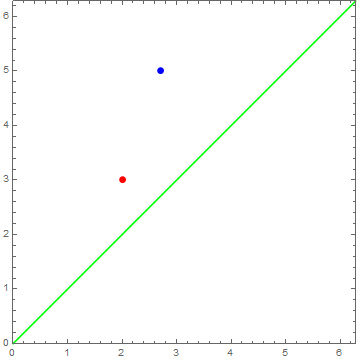
2、在球面上的表现为《Viviani curve》。

ParametricPlot3D[r[{u, u}], {u, 0, 2 Pi}]

3、如果v=Pi + Sin[6 u]/6，就在uv平面上画出一条正弦曲线。

4、它在球面上就表现为一条球面波动曲线。

5、uv平面上的正方形的参数方程是：

Pi - {Abs[Sin[tt]] Sin[tt], Abs[Cos[tt]] Cos[tt]}

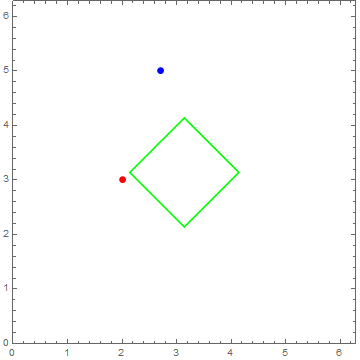
6、在球面上表现为：

ParametricPlot3D[

 r[Pi - {Abs[Sin[tt]] Sin[tt], Abs[Cos[tt]] Cos[tt]}], {tt, 0, 2 Pi}]

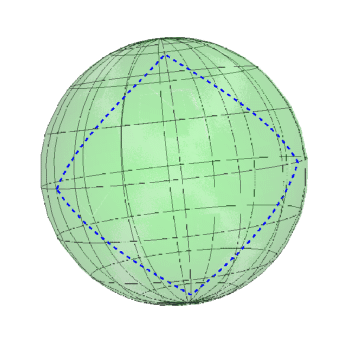
7、这样一组同心的正方形，在球面上表现如下：

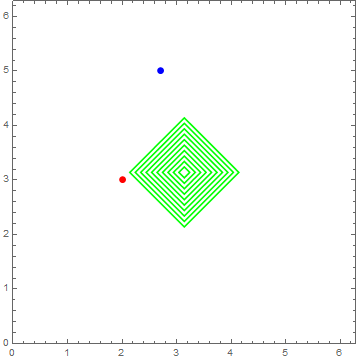
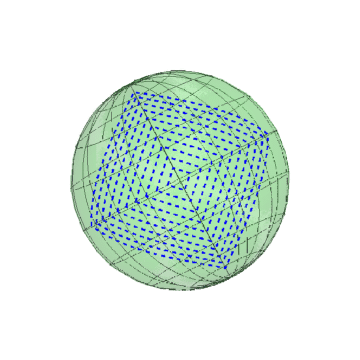
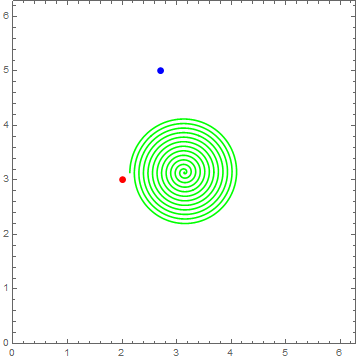
8、螺旋线：

Pi - u/(2 Pi) {Cos[12*u], Sin[12*u]}