Matlab中的FFT函数示例。
1、在命令行窗口,输入如下命令:
load sunspot.dat
year = sunspot(:,1);
relNums = sunspot(:,2);
plot(year,relNums)
title('Sunspot Data')
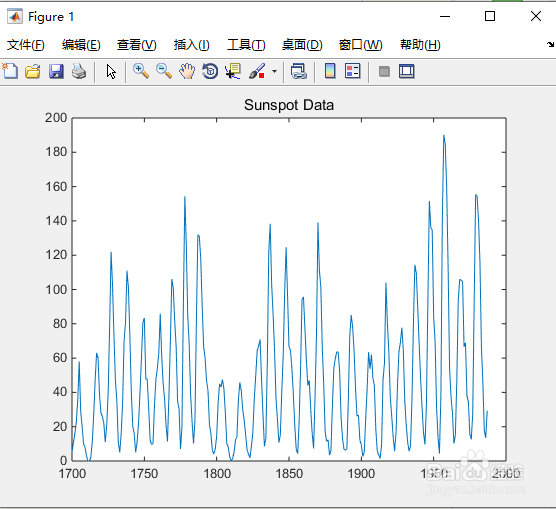
如图1所示。
2、按“Enter键”,得到Figure1。
如图2所示。
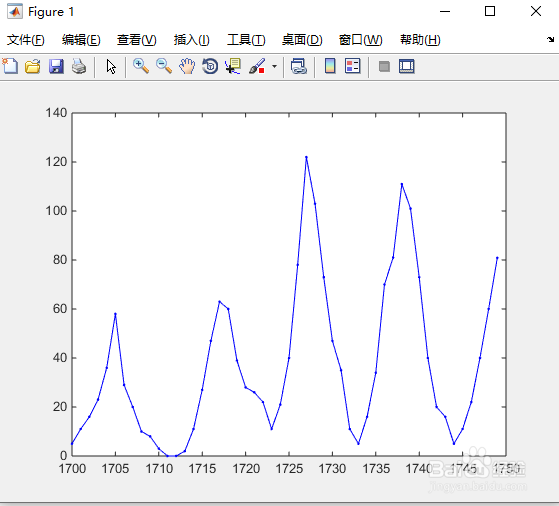
3、以下是前50年的近况。
在命令行窗口,输入如下命令:
plot(year(1:50),relNums(1:50),'b.-');
如图3所示。
4、信号处理的基本工具是快速傅立叶变换(FFT)。要获取太阳黑子数据的FFT,请键入以下内容。
Y的第一部分Y(1)只是数据的和,可以删除。
在命令行窗口,输入如下命令:
Y = fft(relNums);
Y(1) = [];
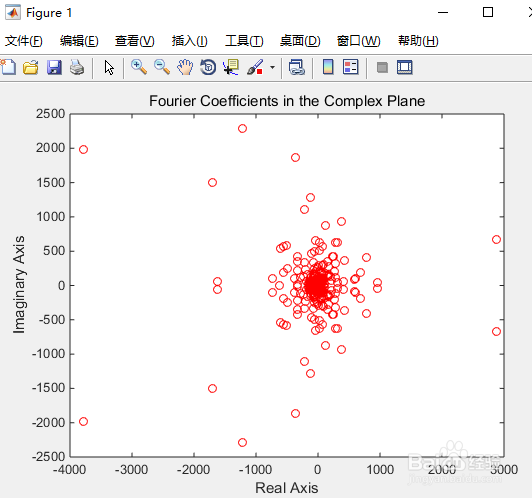
复平面上Fourier系数(由Y给出)的分布图很漂亮,但很难解释。我们需要一种更有用的方法来检查Y中的数据。
在命令行窗口,输入如下命令:
plot(Y,'ro')
title('Fourier Coefficients in the Complex Plane');
xlabel('Real Axis');
ylabel('Imaginary Axis');
如图4所示。
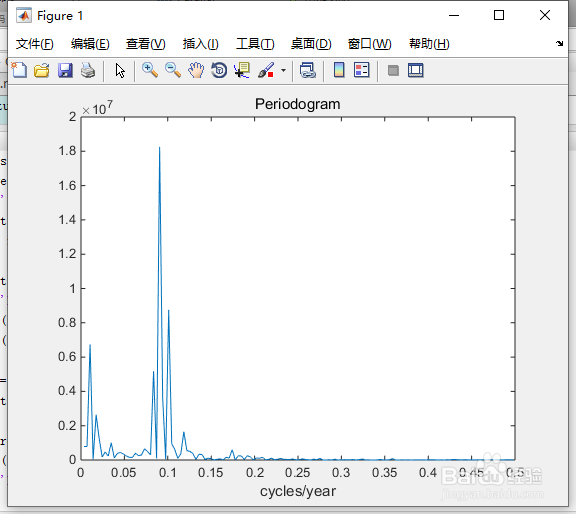
5、Y的复震级平方称为功率,功率与频率的关系图称为“周期图”。
在命令行窗口,输入如下命令:
n = length(Y);
power = abs(Y(1:floor(n/2))).^2;
nyquist = 1/2;
freq = (1:n/2)/(n/2)*nyquist;
plot(freq,power)
xlabel('cycles/year')
title('Periodogram')
如图5所示。
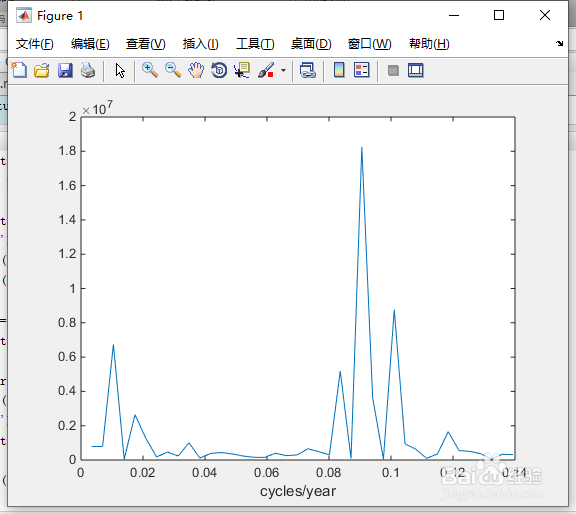
6、周期/年的比例有些不方便。
我们可以用年/周期来作图,估计一个周期的长度。
在命令行窗口,输入如下命令:
plot(freq(1:40),power(1:40))
xlabel('cycles/year')
如图6所示。
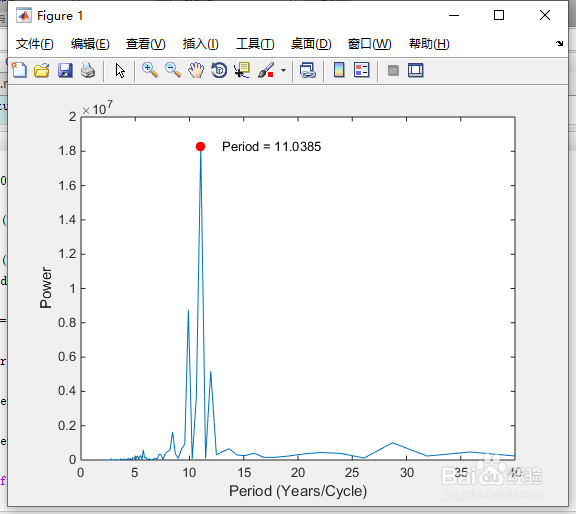
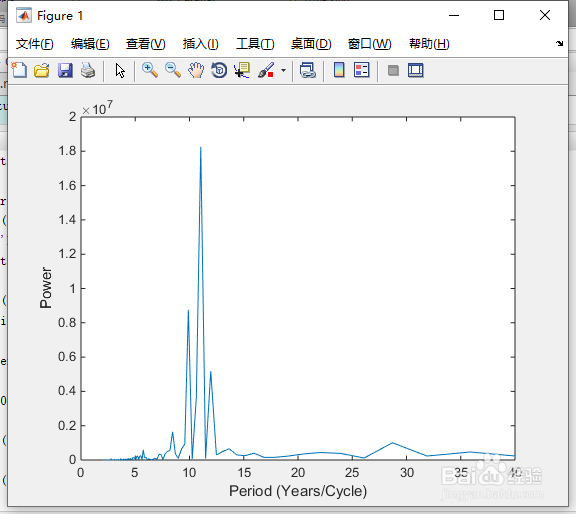
7、为了方便起见,我们绘制了功率与周期的关系图(其中period=1./freq)。正如预期的那样,有一个非常显著的周期,其长度约为11年。
在命令行窗口,输入如下命令:
period = 1./freq;
plot(period,power);
axis([0 40 0 2e+7]);
ylabel('Power');
xlabel('Period (Years/Cycle)');
如图7所示。
8、最后,我们可以通过选择最强的频率来更精确地确定周期长度。红点定位这一点。
在命令行窗口,输入如下命令:
hold on;
index = find(power == max(power));
mainPeriodStr = num2str(period(index));
plot(period(index),power(index),'r.', 'MarkerSize',25);
text(period(index)+2,power(index),['Period = ',mainPeriodStr]);
hold off;
如图8所示。