matlab中怎么使用微分方程?
1、初值问题
范德波德莫是定义范德波尔方程的函数。
type vanderpoldemo
2、按“Enter”键。
如图1所示。

3、方程被写成一个二阶一阶赋格。对于参数Mu的不同值,对它们进行计算。为了加快积分速度,我们根据参数μ的值来选择合适的求解器。
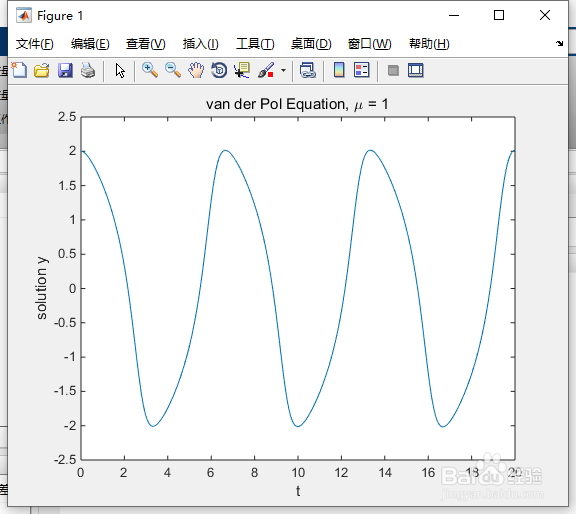
对于μ=1,任意一个MATLAB的ODE解算器都能有效地求解范德波尔方程。下面使用的ODE45求解器就是这样一个例子。方程在[0,20]域内求解。
tspan = [0, 20];
y0 = [2; 0];
Mu = 1;
ode = @(t,y) vanderpoldemo(t,y,Mu);
[t,y] = ode45(ode, tspan, y0);
% Plot of the solution
plot(t,y(:,1))
xlabel('t')
ylabel('solution y')
title('van der Pol Equation, \mu = 1')
4、按“Enter”键。
得图2所示。
5、对于较大的μ量级,问题变得棘手。快速积分需要特殊的数值方法。ODe15S、ODe23S、ODe23T和ODe23Tb能有效地解决刚性问题。
这里是一个解决范德波尔方程的μ=1000使用ODe15S。
tspan = [0, 3000];
y0 = [2; 0];
Mu = 1000;
ode = @(t,y) vanderpoldemo(t,y,Mu);
[t,y] = ode15s(ode, tspan, y0);
plot(t,y(:,1))
title('van der Pol Equation, \mu = 1000')
axis([0 3000 -3 3])
xlabel('t')
ylabel('solution y')
6、按“Enter”键。
得图3所示。

7、边值问题
Bvp4C求解常微分方程边值问题。
示例函数TWOODE有一个微分方程,它被写成二阶一阶ODEs系统。
type twoode
8、TWOBC的边界条件。
type twobc
9、在使用Bvp4C之前,我们必须为我们想要在网格上表示的解决方案提供一个猜测。然后求解器调整网格以细化解决方案。
BVPINIT以求解器Bvp4C所需的形式集合了最初的猜测。对于初始网格[0 1 2 3 4]和常量猜测的y(x)=1,y'(x)=0,像这样调用BVPINIT:
solinit = bvpinit([0 1 2 3 4],[1; 0]);
10、有了这个初步的猜想,我们就可以解决Bvp4C的问题。
溶液溶胶(如下图),然后用DEVAL计算并绘制。
sol = bvp4c(@twoode, @twobc, solinit);
xint = linspace(0, 4, 50);
yint = deval(sol, xint);
plot(xint, yint(1,:),'b');
xlabel('x')
ylabel('solution y')
hold on
11、按“Enter”键。
得图4所示。

12、这个特殊的边值问题正好有两个解。得到的另一个解是对
y(x) = -1, y'(x) = 0
像以前一样画图。
solinit = bvpinit([0 1 2 3 4],[-1; 0]);
sol = bvp4c(@twoode,@twobc,solinit);
xint = linspace(0,4,50);
yint = deval(sol,xint);
plot(xint,yint(1,:),'r');
hold off
13、按“Enter”键。
得图5所示。

14、偏微分方程
PDEPE在一个空间变量和时间内求解偏微分方程。
示例PDex1、PDex2、PDex3,PDex4,PDex5形成了一个关于使用PDEPE的小型教程。浏览这些函数以获取更多示例。
此示例问题使用了函数PDex1Pde、PDex1IC和PDex1BC。
PDex1Pde定义微分方程。
type pdex1pde
15、PDex1IC设置初始条件。
type pdex1ic
16、PDex1BC设置边界条件。
type pdex1bc
17、PDEPE需要x(空间离散化)和t(希望得到解决方案快照的时间矢量)。我们使用20个节点的网格来解决这个问题,并在5个t值处请求解决方案。最后,我们提取并绘制溶液的第一组分。
x = linspace(0,1,20);
t = [0 0.5 1 1.5 2];
sol = pdepe(0,@pdex1pde,@pdex1ic,@pdex1bc,x,t);
u1 = sol(:,:,1);
surf(x,t,u1);
xlabel('x');
ylabel('t');
zlabel('u');
18、按“Enter”键。
得图6所示。
