求一阶非齐次线性微分方程的通解的应用举例
1、一阶非齐次线性微分方程的解析式为:
y'+p(x)=q(x),
则其通解表达式如下:
y=e^[-∫p(x)]dx{∫q(x)*e^[∫p(x)dx]dx+c}.

1、本例中,p(x)=2x,q(x)=4x.

2、本例中,p(x)=-1/x,q(x)=2x^2.

3、本例中,p(x)=1/x,q(x)=sinx/x.
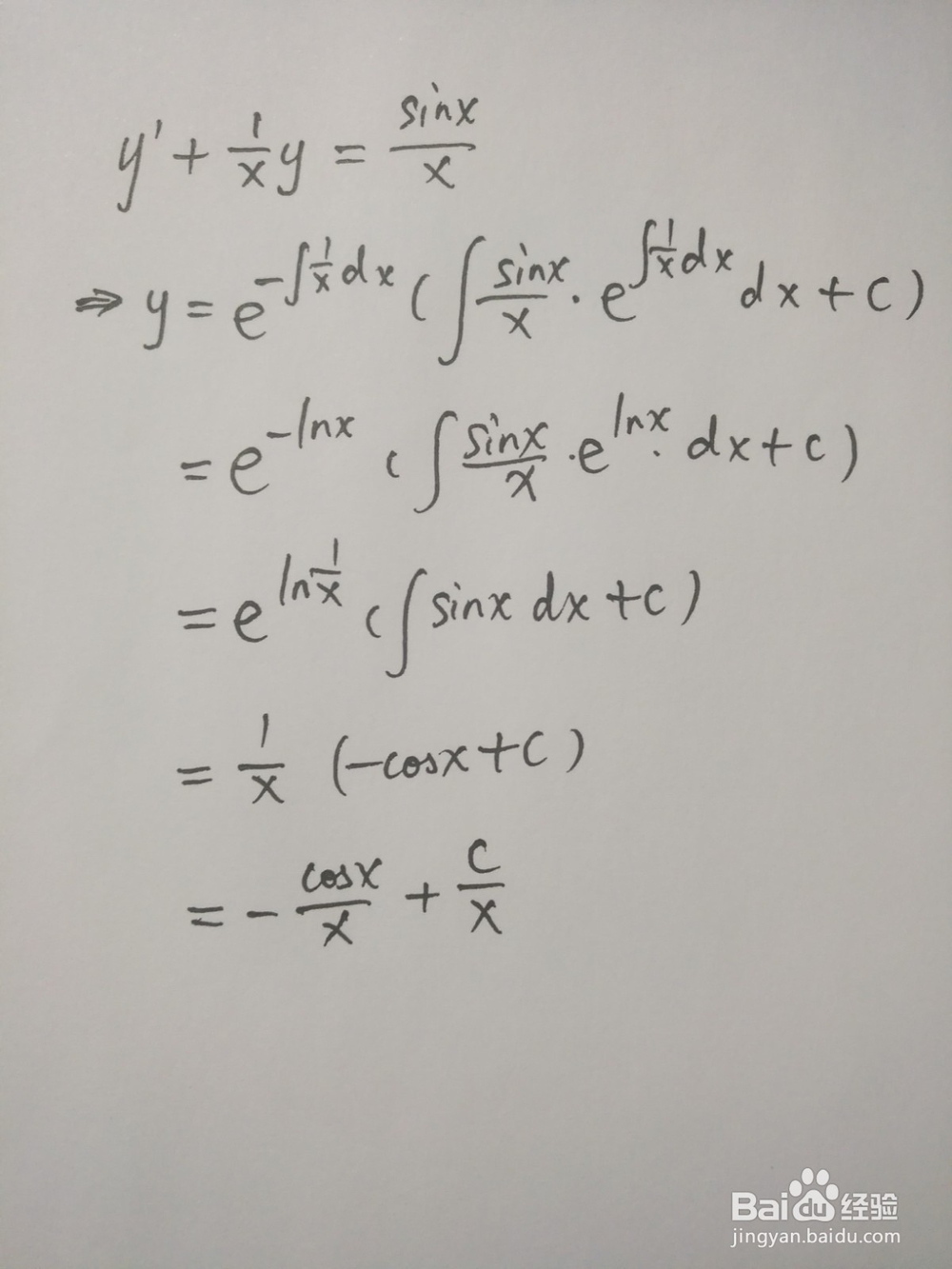
4、本例中,先要将y'前面的系数x变形除后,得到:
p(x)=1/x,q(x)=e^x/x.

5、本例中,p(x)=-a,q(x)=e^mx.

6、此例中,要反过来用一阶非齐次线性微分方程的通解公式,其中:
p(y)=-3/y,q(y)=-y/2.

1、本例中p(x)=1/x,q(x)=4/x,求满足y(x=1)=0时的特解。

2、本例中p(x)=(2-3x^2)/x^3,q(x)=1,求满足y(x=1)=0时的特解。
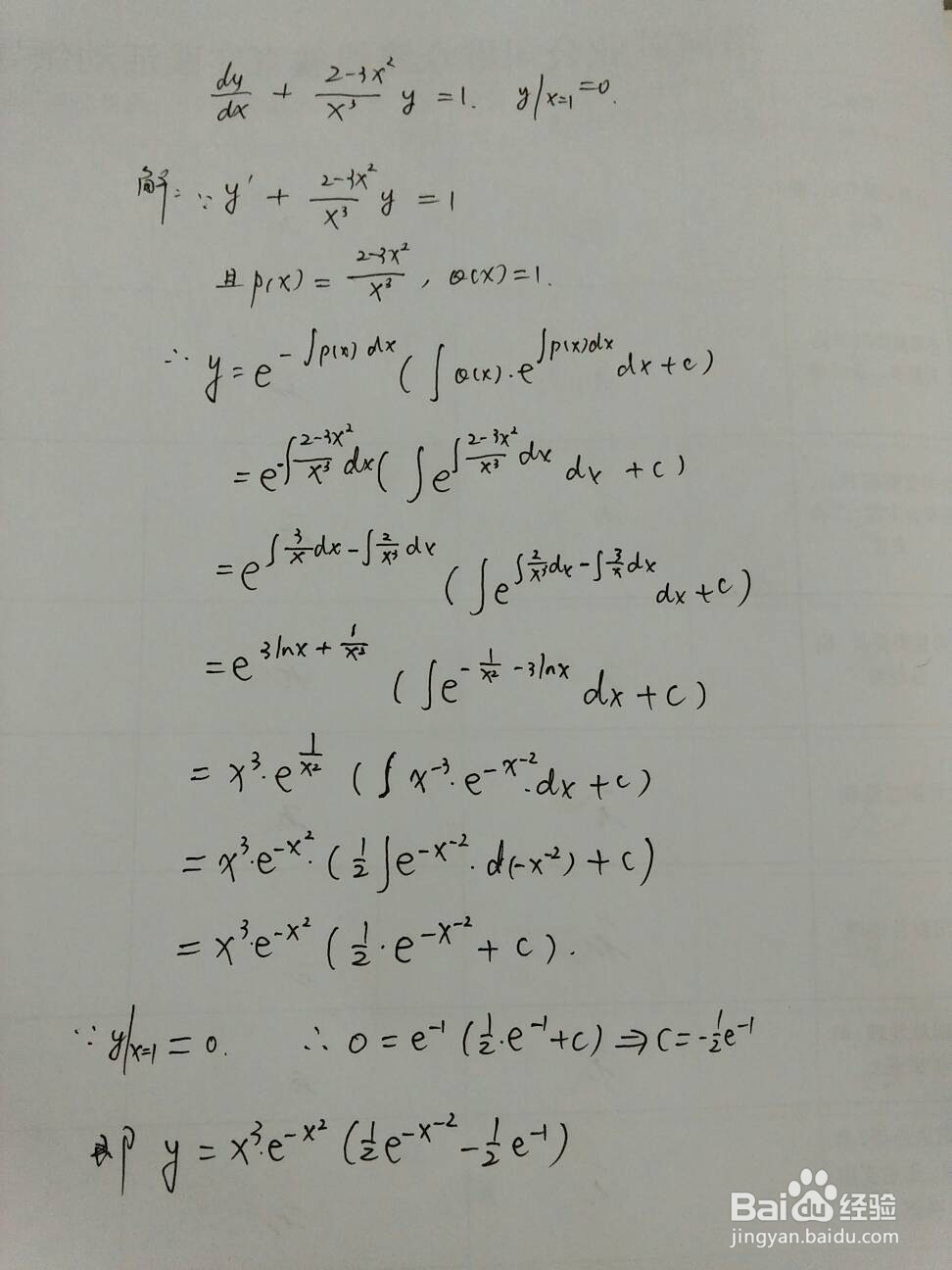
1、y''+y'/x=4,此时先对y'按照通式公式来求解,再对y'积分求解得到y,通解中含有两个常数系数c1和c2,此时P=1/x,Q=4。

2、y''=y'+x,此时先对y'按照通式公式来求解,再对y'积分求解得到y,通解中含有两个常数系数c1和c2,此时P=-1,Q=x。
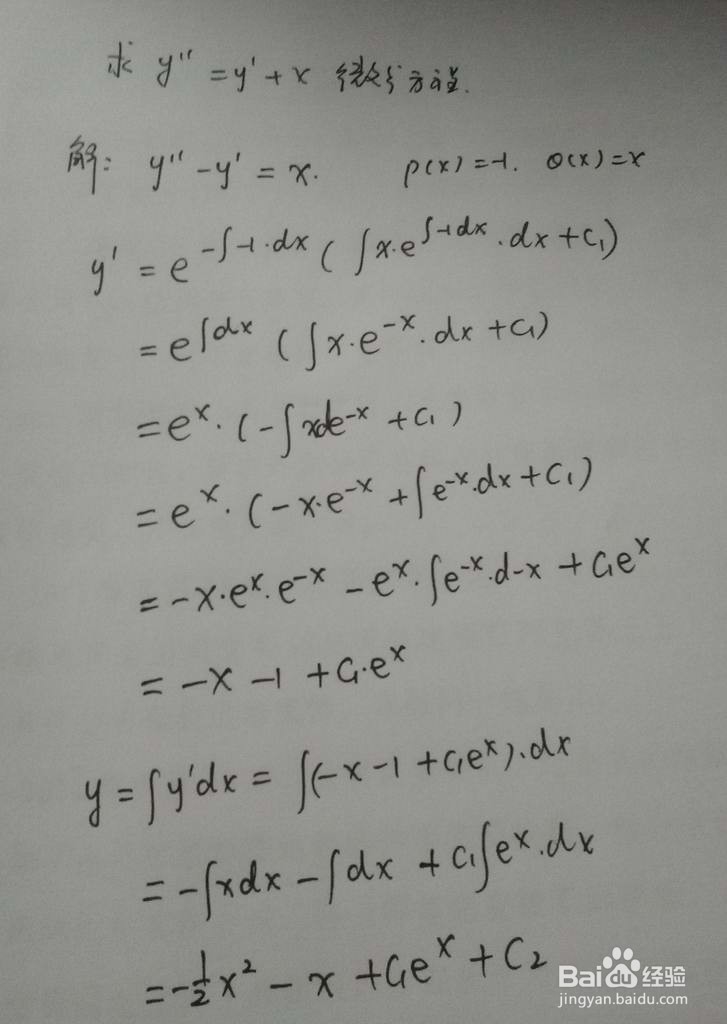
3、xy''+y'=lnx,此时先对y'按照通式公式来求解,再对y'积分求解得到y,通解中含有两个常数系数c1和c2,此时P=1/x,Q=lnx/x.
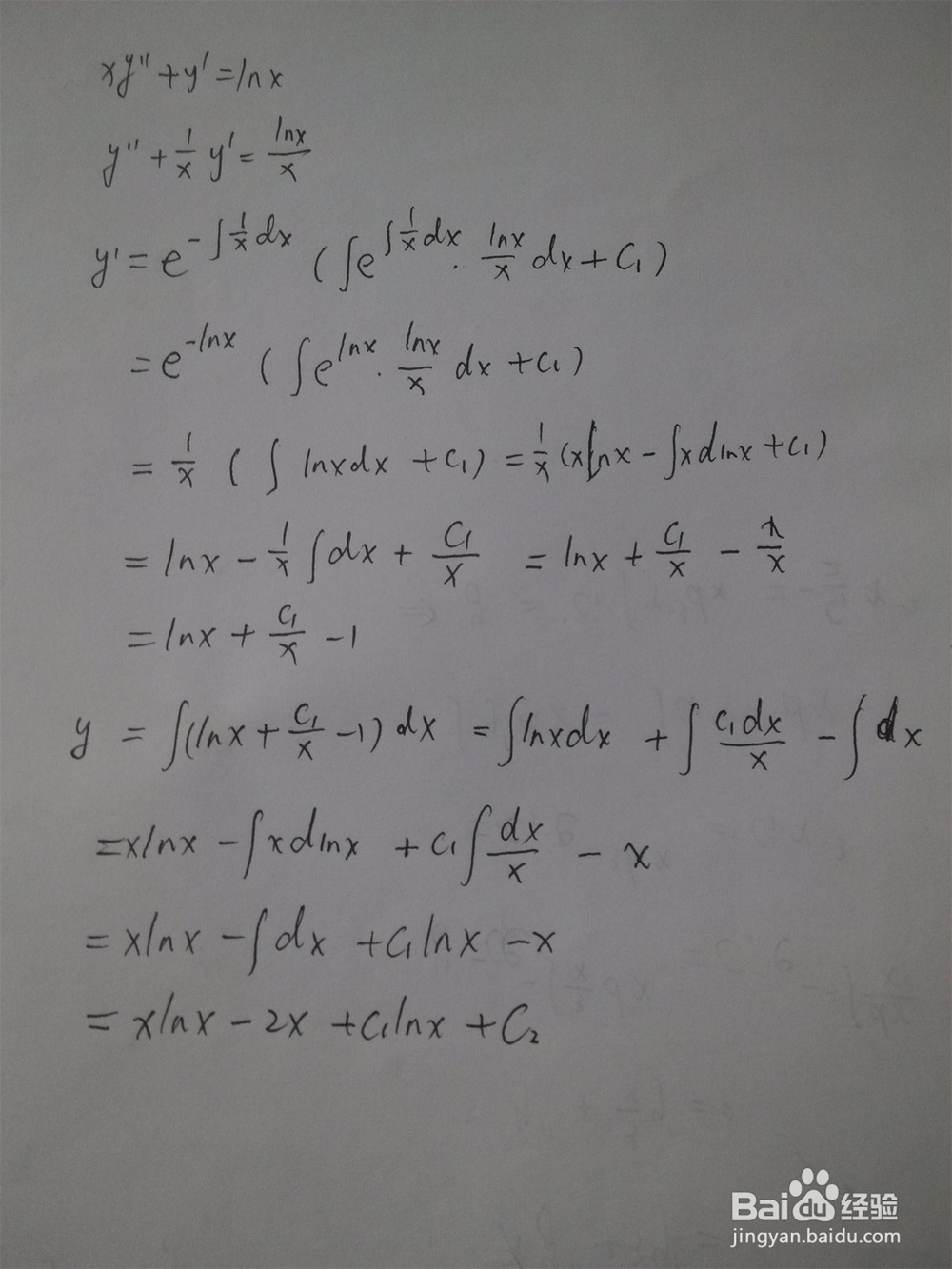
声明:本网站引用、摘录或转载内容仅供网站访问者交流或参考,不代表本站立场,如存在版权或非法内容,请联系站长删除,联系邮箱:site.kefu@qq.com。