求一次函数的解析式的方法
一次函数及其图象是初中代数的重要内容,也是高中解析几何的基石,更是中考的重点考查内容。现在我通过几个经典题型来为大家介绍几种求一次函数解析式的常用方法。
工具/原料
纸
笔
方法/步骤
定义型:
已知函数y=(m-3)x^(m^2-8)+3是一次函数,求其解析式。
解:由一次函数定义知m^2-8=1,m-3≠0
所以m=±3,m≠3
所以m=-3
故一次函数的解析式为y=-6x+3。

点斜型:
已知一次函数y=kx-3的图像过点(2,-1),求这个函数的解析式。
解:因为一次函数y=kx-3的图像过点(2,-1)
所以-1=2k-3,即k=1
故这个函数的解析式为y=x-3。

两点型:
已知某个一次函数的图像与x轴、y轴的交点坐标分别是(-2,0)、(0,4),求这个一次函数的解析式。
解:设这个一次函数的解析式为y=kx+b
由题意得0=-2k+b,4=b
所以k=2,b=4
故这个一次函数的解析式为y=2x+4。

图像型:
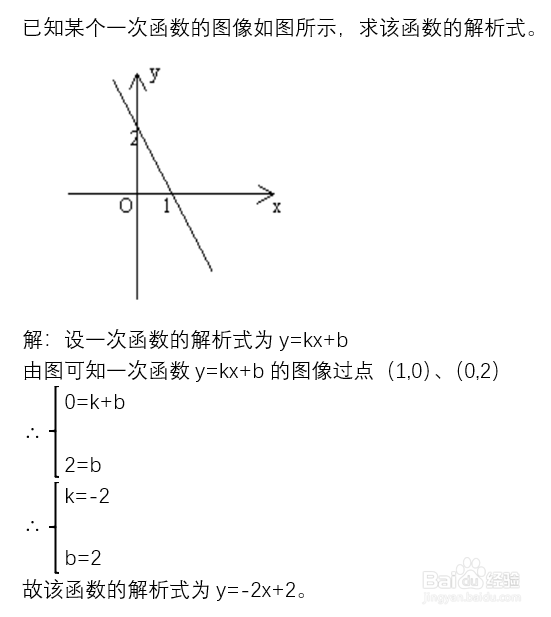
已知某个一次函数的图像如图所示,求该函数的解析式。
解:设一次函数的解析式为y=kx+b
由图可知一次函数y=kx+b的图像过点(1,0)、(0,2)
所以可得0=k+b,2=b
所以k=-2,b=2
故该函数的解析式为y=-2x+2。
斜截型:
已知直线y=kx+b与直线y=-2x平行,且在y轴上的截距为2,求直线的解析式。
解:当k1=k2,b1≠b2时,直线y=k1x+b1与直线y=k2x+b2平行
因为直线y=kx+b与直线y=-2x平行,所以k=-2
又因为直线y=kx+b在y轴上的截距为2,所以b=2
故直线的解析式为y=-2x+2。

注意事项
一次函数:y=kx+b(k,b是常数,k≠0)
声明:本网站引用、摘录或转载内容仅供网站访问者交流或参考,不代表本站立场,如存在版权或非法内容,请联系站长删除,联系邮箱:site.kefu@qq.com。
阅读量:72
阅读量:28
阅读量:129
阅读量:58
阅读量:27