【Mathematica】怎么计算矩阵生成的群?
1、给定矩阵:
A = {{1, 1}, {-1, 0}};
计算矩阵的幂,其实就是重复乘以这个矩阵:
MatrixPower[A, n]
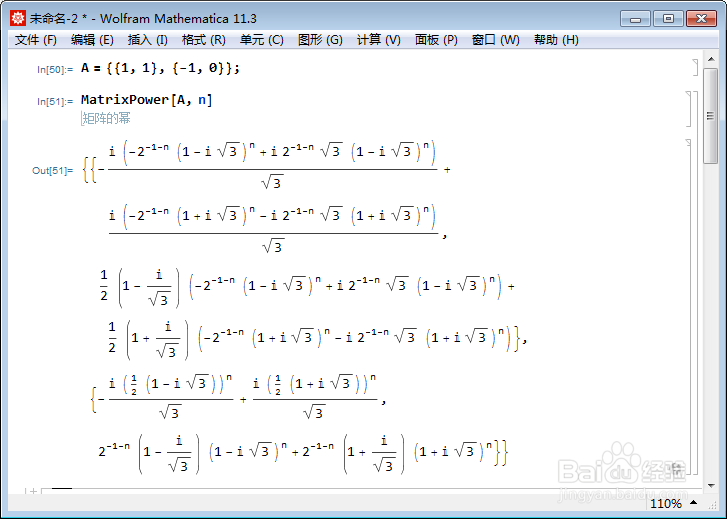
2、这里的n当然可以是小数:
MatrixPower[A, 1/2]
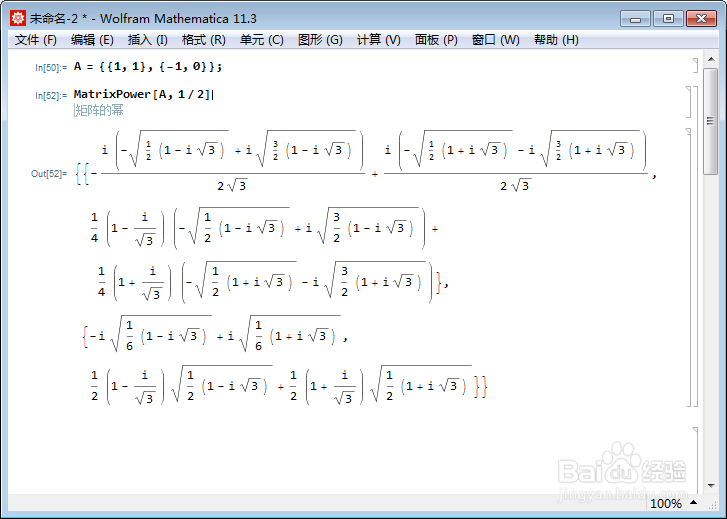
3、n也可以为复数:
MatrixPower[A, I]
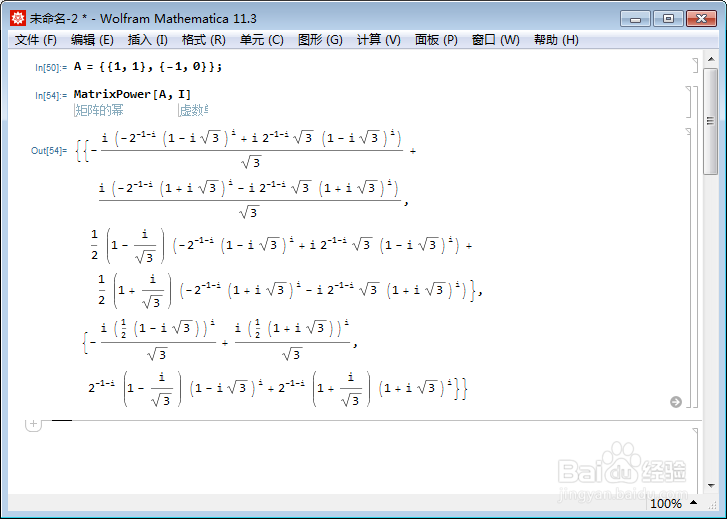
4、不过涉及到群,自然只考虑n是整数:
MatrixPower[A, n] // FullSimplify
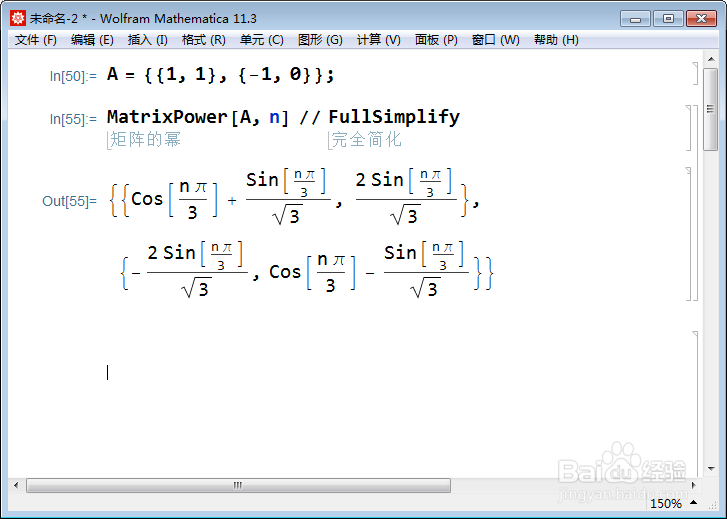
5、解方程组:
Solve[{Cos[(n*Pi)/3] + Sin[(n *Pi)/3]/Sqrt[3] == 1,
(2 Sin[(n*Pi)/3])/Sqrt[3] == 0}, n]
答案是,n为6的倍数。

6、这样,可以确定这个矩阵生成一个6阶群。
MatrixForm[MatrixPower[A, #]] & /@ Range[6]

7、这个群里面必定有2阶元素和3阶元素:
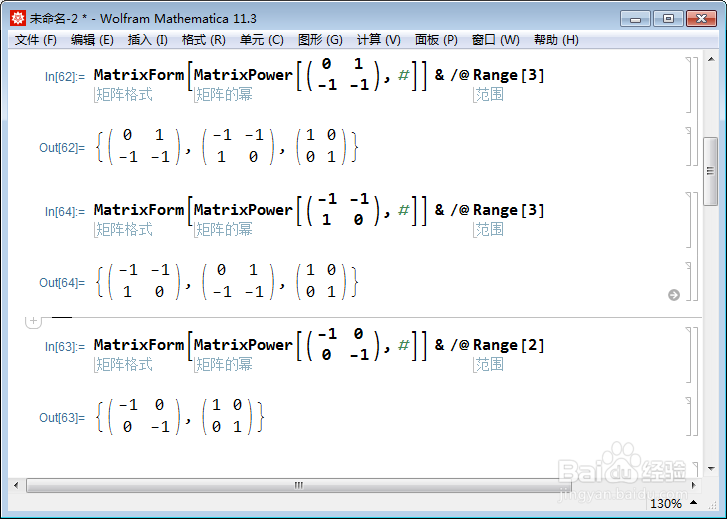
声明:本网站引用、摘录或转载内容仅供网站访问者交流或参考,不代表本站立场,如存在版权或非法内容,请联系站长删除,联系邮箱:site.kefu@qq.com。
阅读量:182
阅读量:159
阅读量:75
阅读量:173
阅读量:111