【matlab数字图像处理实验】边缘检测

1、常用的梯度算子

 

2、利用edge函数实现

 

I=imread('fabric.png');%读取图像

 

K=rgb2gray(I);

 

BW1 = edge(K,'roberts',0.08);

 

%进行Roberts 算子边缘检测，门限值采用默认值

 

BW2 = edge(K,'prewitt', 0.05);

 

%进行Prewitt 算子边缘检测，门限值采用默认值

 

BW3 = edge(K,'sobel', 0.04);

 

%进行 Sobel算子边缘检测，门限值采用默认值

 

figure,imshow(BW1,[]),title('Roberts 算子图像');

 

figure,imshow(BW2,[]),title('Prewitt 算子图像');

 

figure,imshow(BW3,[]),title('Sobel算子图像');

 

Roberts 算子图像

 

Prewitt 算子图像

 

Sobel算子图像

 

 

3、利用模版处理

 

Roberts 算子

 

I=imread('fabric.png');

 

K=rgb2gray(I);

 

BW1=[1,0;0,-1];

 

BW2=[0,1;-1,0];

 

J1=filter2(BW1,K);

 

J2=filter2(BW2,K);

 

K1=double(J1);

 

K2=double(J2);

 

M=(abs(K1) +abs(K2));

 

figure,imshow(uint8(M))

 

Prewitt 算子

 

I=imread('fabric.png');

 

K=rgb2gray(I);

 

BW1=[-1,-1,-1;0,0,0;1,1,1];

 

BW2=[-1,0,1;-1,0,1;-1,0,1];

 

J1=filter2(BW1,K);

 

J2=filter2(BW2,K);

 

K1=double(J1);

 

K2=double(J2);

 

M=(abs(K1) +abs(K2));

 

figure,imshow(uint8(M))

 

Sobel算子

 

I=imread('fabric.png');

 

K=rgb2gray(I);

 

BW1=[-1,-2,-1;0,0,0;1,2,1];

 

BW2=[-1,0,1;-2,0,2;-1,0,1];

 

J1=filter2(BW1,K);

 

J2=filter2(BW2,K);

 

K1=double(J1);

 

K2=double(J2);

 

M=(abs(K1) +abs(K2));

 

figure,imshow(uint8(M))

 

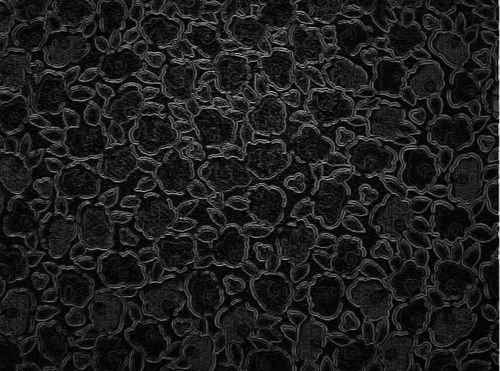
1、图像局部特征的不连续性(相邻区域的交界)称为边缘。边缘位置的微分特性是幅度和方向性(沿边缘方向灰度缓变，垂直方向突变)。边缘位置和导数(微分)间具有一定对应关系，可通过微分进行边缘检测。无噪声时，可用Roberts算子；Prewitt和Sobel算子同时具有平均，即抑制噪声作用；对阶跃状边缘，Roberts得到的边缘宽度≥1个像素，Prewitt和Sobel算子得到的边缘宽度≥2个像素。

2、由实验的效果图像可以知道，在利用edge函数进行相应的算子边缘检测的时候，各算子的差别非常微小，不过由相应的参数，三个算子分别为0.08、0.05、0.04可以知道，Sobel算子在边缘检测中最为敏感，及在同一条件下它的处理效果应该最好。在后面实验部分中，利用“手动”的模版算子进行边缘检测，我们很容易可以看到，Sobel算子的处理效果最好。