使用OpenCV 3.4进行图像的拉伸旋转平移基本处理
1、图像的基本处理1:图像的缩放操作,可以对图像进行放大或缩小,通过实验可以看到缩放的模式使用0时清晰度效果是最差的。
我们需要使用到的OpenCV的函数:
void resize( InputArray src, OutputArray dst, Size dsize, double fx = 0, double fy = 0, int interpolation = INTER_LINEAR );
参数:dsize(0,0)表示Size(round(fx*src.cols), round(fy*src.rows)
参数fx为横轴拉伸比例,fy为纵轴拉伸比率
实现的主要函数代码:
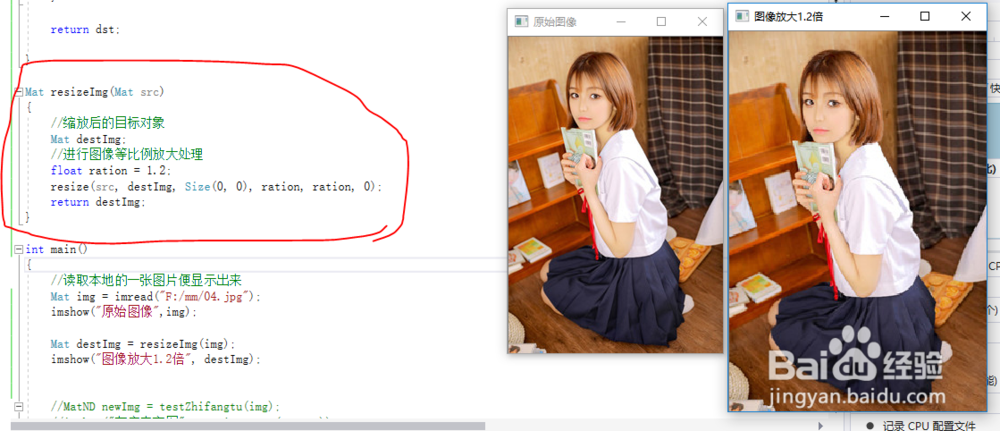
/*参数src: 原图像ration:等比例缩放比率type:缩放的模式 0,1,2,3,4,5,整数 */Mat resizeImg(Mat src,double ration,int type){ //缩放后的目标对象 Mat destImg; //进行图像等比例放大处理 //邻近模式 resize(src, destImg, Size(0, 0), ration, ration, type);
return destImg;}
int main(){ //读取本地的一张图片便显示出来 Mat img = imread("F:/mm/04.jpg"); imshow("原始图像",img);
Mat destImg = resizeImg(img,1.2,0); imshow("图像放大1.2倍 0模式:", destImg); destImg = resizeImg(img, 1.2, 1); imshow("图像放大1.2倍 1模式:", destImg); destImg = resizeImg(img, 1.2, 2); imshow("图像放大1.2倍 2模式:", destImg); destImg = resizeImg(img, 1.2, 3); imshow("图像放大1.2倍 3模式:", destImg); destImg = resizeImg(img, 1.2, 4); imshow("图像放大1.2倍 4模式:", destImg); destImg = resizeImg(img, 1.2, 5); imshow("图像放大1.2倍 5模式:", destImg);
waitKey(0); return 0;}

2、图像的基本处理2:图像的平移操作,可以实现图像按照x、y轴两个方向平移。
使用到的关键函数f:
void warpAffine( InputArray src, OutputArray dst, InputArray M, Size dsize, int flags = INTER_LINEAR, int borderMode = BORDER_CONSTANT, const Scalar& borderValue = Scalar());
实现的关键代码:
Mat pingyiImg(Mat src){ Mat destImg; //平移矩阵对象,x横轴方向平移50,y轴方向平移50 Mat moving = (Mat_<double>(2, 3) << 1, 0, 50, 0, 1, 50); warpAffine(src, destImg, moving, src.size()); return destImg;}int main(){ //读取本地的一张图片便显示出来 Mat img = imread("F:/mm/04.jpg"); imshow("原始图像",img);
Mat destImg = pingyiImg(img); imshow("图像平移:", destImg);
waitKey(0); return 0;}

3、图像的基本处理3:图像旋转,通过旋转可以对图像进行任意角度的旋转,用以矫正图像的倾斜度等。
实现函数代码:
Mat rotateImg(Mat src){ Mat destImg; //获取变换矩阵,参数一:旋转中心坐标,参数二:旋转角度,参数三:图像缩放比例 Mat roateM = getRotationMatrix2D(Point2f(src.cols/2, src.rows/2), 60, 1); warpAffine(src, destImg, roateM, src.size()); return destImg;}

4、图像的基本处理4:基于三组点的仿射变换图像
关键函数代码:
/*目标图和源图像进行三组点计算的仿射变换*/Mat transformImg(Mat src){ Mat destImg; Point2f srcTrig[3]; Point2f dstTrig[3];
srcTrig[0] = Point2f(0, 0); srcTrig[1] = Point2f(src.cols - 1, 0); srcTrig[2] = Point2f(0, src.rows - 1);
dstTrig[0] = Point2f(0, src.rows*0.55); dstTrig[1] = Point2f(src.cols*0.65, src.rows*0.55); dstTrig[2] = Point2f(src.cols*0.65, src.rows*0.25); Mat transformM = getAffineTransform(srcTrig, dstTrig); //获取变换矩阵 warpAffine(src, destImg, transformM, src.size()); return destImg;}

5、图像基本处理5: 图像镜像,可以对图像进行水平、垂直、水平+垂直进行镜像处理
关键函数代码:
Mat mirrorImg(Mat src){ Mat destImg; //图像水平镜像 Mat matrixX = (Mat_<double>(2, 3) << -1, 0, src.cols, 0, 1, 0); warpAffine(src, destImg, matrixX, src.size()); imshow("水平方向镜像", destImg);
Mat matrixY = (Mat_<double>(2, 3) << 1, 0, 0, 0, -1, src.rows); warpAffine(src, destImg, matrixY, src.size()); imshow("垂直平方向镜像", destImg); Mat matrixXY = (Mat_<double>(2, 3) << -1, 0, src.cols, 0, -1, src.rows); //水平+垂直
warpAffine(src, destImg, matrixXY, src.size()); imshow("水平和垂直平方向镜像", destImg); return destImg;}

6、图像基本处理6:图像透视转换处理
关键函数:
Mat toushiImg(Mat src){ Mat destImg; Point2f srcMatric[4]; Point2f destMatric[4];
srcMatric[0] = Point(0, 0); srcMatric[1] = Point(src.cols - 1, 0); srcMatric[2] = Point(0, src.rows - 1); srcMatric[3] = Point(src.cols - 1, src.rows - 1); destMatric[0] = Point(src.cols*0.4, src.rows*0.3); destMatric[1] = Point(src.cols*0.7, src.rows*0.1); destMatric[2] = Point(src.cols*0.1, src.rows*0.8); destMatric[3] = Point(src.cols*0.8, src.rows*0.9); Mat toushiMatric = getPerspectiveTransform(srcMatric, destMatric); warpPerspective(src, destImg, toushiMatric, src.size()); return destImg;}
