矩阵的转置怎么求

1、定义:

把矩阵 A 的行换成同序数的列得到的矩阵,叫做 A 的转置矩阵,记作 AT。

例如：

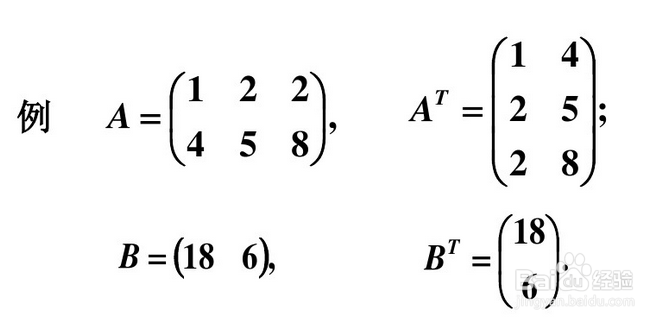
2、矩阵转置的运算性质

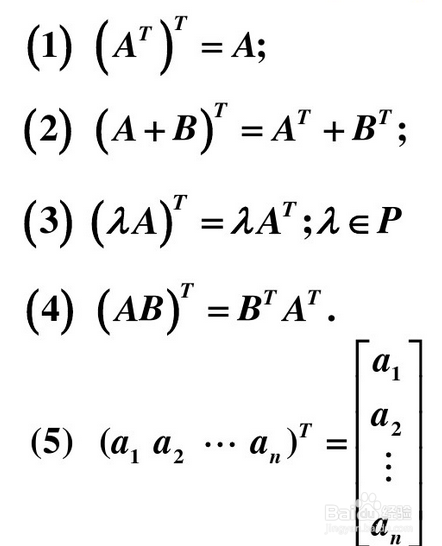
3、性质4的证明（这里只证明第4点）：

4、性质4的推广：

有限个矩阵乘积的转置

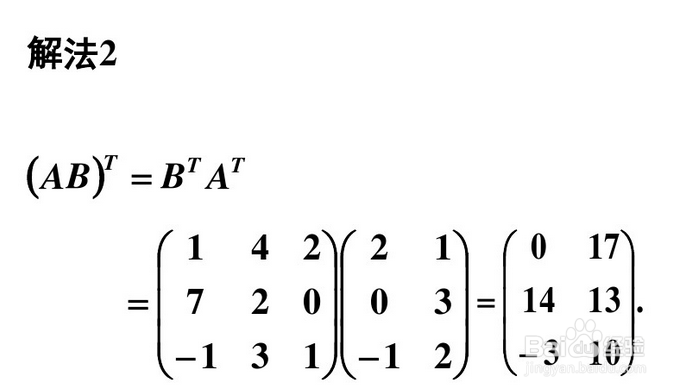
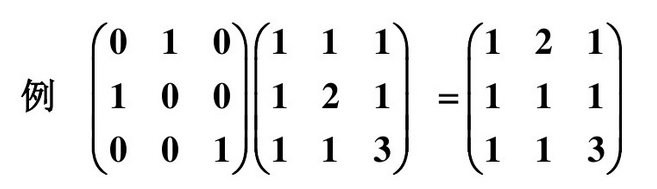
5、还有对称阵：

6、注：对称 矩阵的乘积不一定是对称矩阵

1、程序语言矩阵转置都大同小异，只是语法稍有的不同，以下以二维数组为例，实现矩阵转置：

声明一个二维数组：

$a = array(array(1,2),array(3,4));

输出矩阵：

foreach($a as $value){

   foreach($value as $key => $v){

        echo $v;

   }

   echo '<br />';

}

输出结果：

2、转置：

foreach($a as $keyi => $value){

  foreach($value as $keyj => $v){

    $a1[$keyj][$keyi] = $v;

  }

}

输出转置后的结果：

foreach($a1 as $value){

  foreach($value as $key => $v){

    echo $v;

  }

  echo '<br />';

}

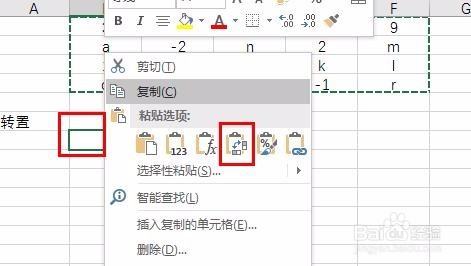
1、先复制需要转置的数据矩阵：

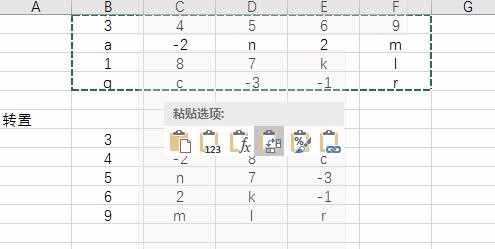
2、然后选择一个空白单元格，单击右键-选择粘贴复制下面第四个图标(转置)：

结果就出来了

1、三元组稀疏矩阵的快速转置算法在《数据结构》课程中是一个难点，处理这个知识点很费时间，这里就不介绍了，有兴趣的可以买相关的书去看。