（x-t）f（t）dt从0到x的积分的导是什么

如图所示：

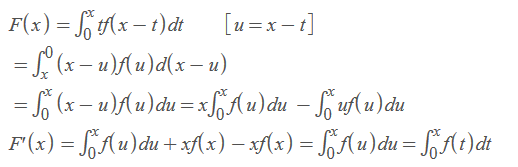
求导是数学计算中的一个计算方法，它的定义就是，当自变量的增量趋于零时，因变量的增量与自变量的增量之商的极限。在一个函数存在导数时，称这个函数可导或者可微分。可导的函数一定连续。不连续的函数一定不可导。

基本求导公式：

给出自变量增量 

得出函数增量 

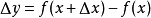
作商 

求极限 

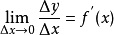
扩展资料：

函数 

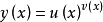
导数公式：

1.C'=0(C为常数)；

2.(Xn)'=nX(n-1) (n∈R)；

3.(sinX)'=cosX；

4.(cosX)'=-sinX；

5.(aX)'=aXIna （ln为自然对数)；

6.(logaX)'=（1/X)logae=1/(Xlna) (a>0，且a≠1)；

7.(tanX)'=1/(cosX)2=(secX)2

8.(cotX)'=-1/(sinX)2=-(cscX)2

9.(secX)'=tanX secX；

10.(cscX)'=-cotX cscX；

参考资料：百度百科——求导