高中数学必修二立体几何中的向量方法_经典案例

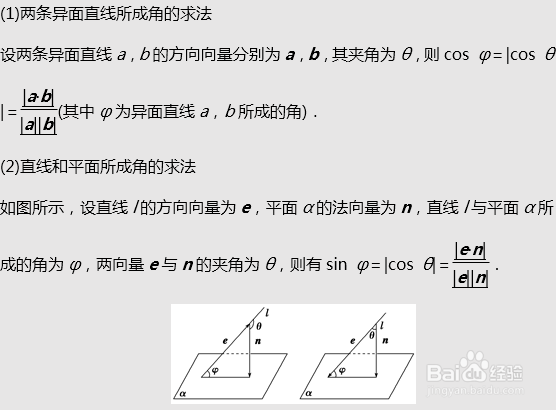
1、1．空间向量与空间角的关系

1

1、1、异面直线所成的角

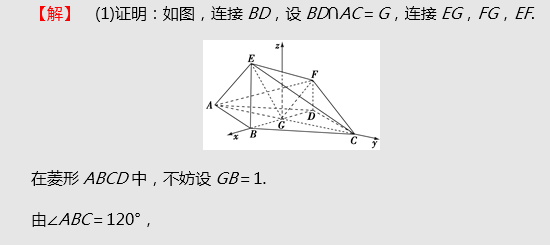
(2015·高考全国卷Ⅰ)如图，四边形ABCD为菱形，∠ABC＝120°，E，F是平面ABCD同一侧的两点，BE⊥平面ABCD，DF⊥平面ABCD，BE＝2DF，AE⊥EC.

(1)证明：平面AEC⊥平面AFC；

(2)求直线AE与直线CF所成角的余弦值．

2、解题方法：

3、2、直线与平面所成的角

  (2017·高考浙江卷)如图，已知四棱锥P­ABCD，△PAD是以AD为斜边的等腰直角三角形，BC∥AD，CD⊥AD，PC＝AD＝2DC＝2CB，E为PD的中点．

(1)证明：CE∥平面PAB；

(2)求直线CE与平面PBC所成角的正弦值．

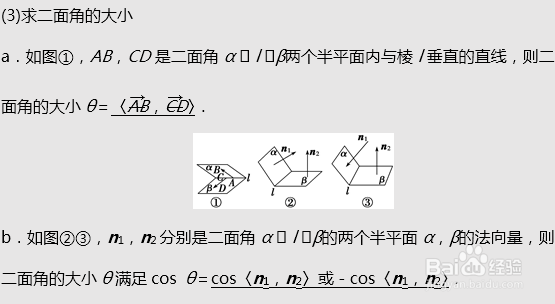
4、3、空间中的距离问题

如图，平面PAD⊥平面ABCD，四边形ABCD为正方形，△PAD是直角三角形，且PA＝AD＝2，E，F，G分别是线段PA，PD，CD的中点．

(1)求证：平面EFG⊥平面PAB；

(2)求点A到平面EFG的距离．

5、解题方法

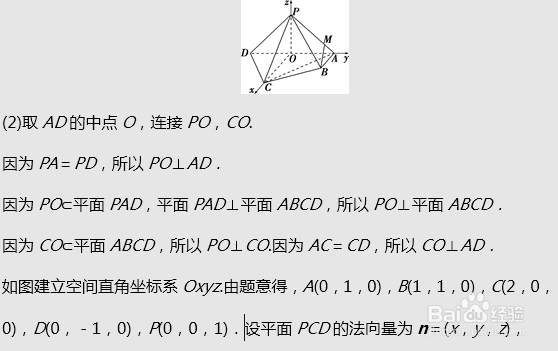
1、(2016·高考北京卷)如图，在四棱锥P­ABCD中，平面PAD⊥平面ABCD，PA⊥PD，PA＝PD，AB⊥AD，AB＝1，AD＝2，AC＝CD＝.

(1)求证：PD⊥平面PAB；

(2)求直线PB与平面PCD所成角的正弦值；

(3)在棱PA上是否存在点M，使得BM∥平面PCD？若存在，求的值；若不存在，说明理由．