MATLAB使用QR分解法求线性方程组的解

1、第一，下图是要求解的线性方程组，等号左边构成系数矩阵A，等号右边构成常数列向量b。该例子参考了王正林等《MATLAB科学计算》的有关内容。

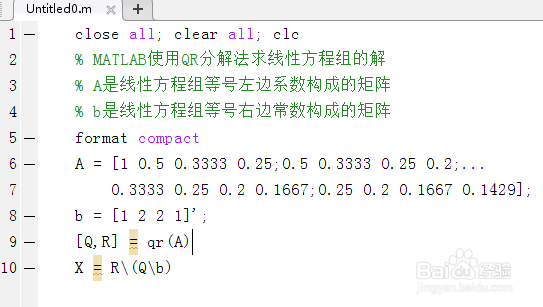
2、第二，启动MATLAB，新建脚本，输入以下代码：

close all; clear all; clc

% MATLAB使用QR分解法求线性方程组的解

% A是线性方程组等号左边系数构成的矩阵

% b是线性方程组等号右边常数构成的矩阵

format compact

A = [1 0.5 0.3333 0.25;0.5 0.3333 0.25 0.2;...

    0.3333 0.25 0.2 0.1667;0.25 0.2 0.1667 0.1429];

b = [1 2 2 1]';

[Q,R] = qr(A)

X = R\(Q\b)

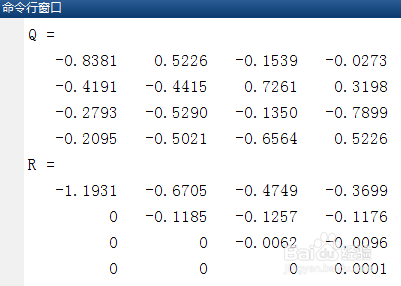
3、第三，保存和运行上述代码，首先得到系数矩阵A分解成的一个正交矩阵Q和一个上三角矩阵R，如下：

Q =

   -0.8381    0.5226   -0.1539   -0.0273

   -0.4191   -0.4415    0.7261    0.3198

   -0.2793   -0.5290   -0.1350   -0.7899

   -0.2095   -0.5021   -0.6564    0.5226

R =

   -1.1931   -0.6705   -0.4749   -0.3699

         0   -0.1185   -0.1257   -0.1176

         0         0   -0.0062   -0.0096

         0         0         0    0.0001

4、第四，同时得到线性方程组的解如下：

X =

   1.0e+03 *

    0.1546

   -1.8578

    4.5882

   -3.0156

5、第五，在命令窗口输入Q*R，验证A是不是等于Q*R，结果显示A=Q*R。

6、第六，在命令窗口输入A*X，验证A*X是不是等于b，结果显示A*X=b，说明QR分解法求解线性方程组是正确的有效的。