实用高效的计算三角形面积的算法

1.普遍的海伦公式

    在网上搜索了一下,关于计算三角形面积的算法,大多采用的是海伦公式,即:

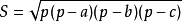
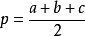
2.为什么不建议使用海伦公式

     但是这条公式在实际开发中运用会存在很多问题,例如:这条公式存在着一个根号,使算法的效率降低了(涉及到了复杂的数学库运算以及浮点数的出现).还有在实际运用中大多数给出的是三角形的3个顶点的坐标,而不是3条边的长度.这意味着如果使用海伦公式进行计算将要开3次根号来计算3条边的长度.然后再求面积,使程序的效率大大的降低了.

3.向量的叉积

      也许许多了解过向量的朋友应该会知道,向量的叉积的一个几何意义,就是 向量a和 向量b的叉积的绝对值表示 以 向量a和 向量b 为两边形成的平行四边形的面积.即:

    S=∣a×b∣

S表示以 向量a 和 向量b 为两边形成的平行四边形的面积

    以此类推就可以得到(1/2) * S就可以表示以 向量a 和 向量b 为两边形成的三角形的面积.

4.具体的实现

    假设三角形的3的顶点分别为P1(x1,y1),P2(x2,y2),P3(x3,y3)

    则向量a 就可以表示为(x2-x1,y2-y1)

      向量b 就可以表示为(x3-x1,y3-y1)

    根据二维向量叉积的运算 

        ∣a×b|=(x2-x1)(y3-y1) - (y2-y1)(x3-x1)

    则这个三角形的面积

        S = |((x2 - x1) * (y3 - y1) - (y2 - y1) * (x3 - x1) ) / 2|

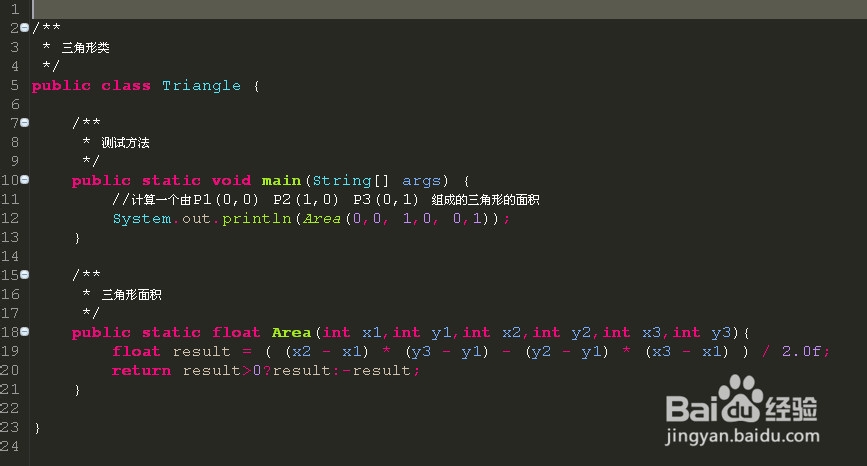
5.Java代码的实现

   直接贴上Java代码:

    /**

      * 三角形类

      */

    public class Triangle {

        /**

         * 测试方法

         */

        public static void main(String[] args) {

        //计算一个由P1(0,0) P2(1,0) P3(0,1) 组成的三角形的面积

        System.out.println(Area(0,0, 1,0, 0,1));

        }

        /**

         * 三角形面积

         */

        public static float Area(int x1,int y1,int x2,int y2,int x3,int y3){

            float result = ( (x2 - x1) * (y3 - y1) - (y2 - y1) * (x3 - x1) ) / 2.0f;

            return result>0?result:-result;

        }

    }

The End

@航行刘 2014/05/11