已知周长L=15，求正多边形和圆的面积

1、正多边形和圆的周长L已知，求正三角形、正方形、正五边形、正六边形和圆的面积。

2、因为周长L=15,所以正

三角形的边长a1=5,       

则正三角形的面积S3为：

S3

=(1/2)*a12*sin60°

=√3*152/36平方单位

≈10.825平方单位。

3、因为周长L=15,所以

正方形的边长a2=15/4,                        

则正方形的面积S4为：

S4=a22

=152/16平方单位

≈14.063平方单位。

4、正五边形的面积：

E L=15

因为周长L=15,所以

正五边形的边长a3=3,

正五边形的每个内角为108°

则∠BAC=72°,

∠EAB=108°-72°=36°,

∠AEM=90°-36°=54°。

5、在直角三角形AEM中：

AM=AE*sin54°=AE*cos36°，EM=AE*sin36°，

三角形AEB的面积为：

S△AEB=2*S△AEM=2*(1/2)*AM*EM,

=a32*sin36°*cos36°

=(1/2)a32*sin72°,

对于等腰梯形ABCD的高MF有：

MF=AC*sin∠BAC=a3*sin72°

6、S□ABCD=(AB+CD)*MF/2

=(2AM+a3)*a3*sin72°/2

=(2a3*cos36°+a3)*a3*sin72°/2

=(1/2)(2cos36°+1)a32*sin72°,

此时正五边形的面积S5= S△AEB+S□ABCD

=(1/2)[a32*sin72°+(2cos36°+1)a32* sin72°]

=a32*sin72°(cos36°+1)平方单位

=152*cos18°(sin54°+1)/25

≈15.484平方单位。

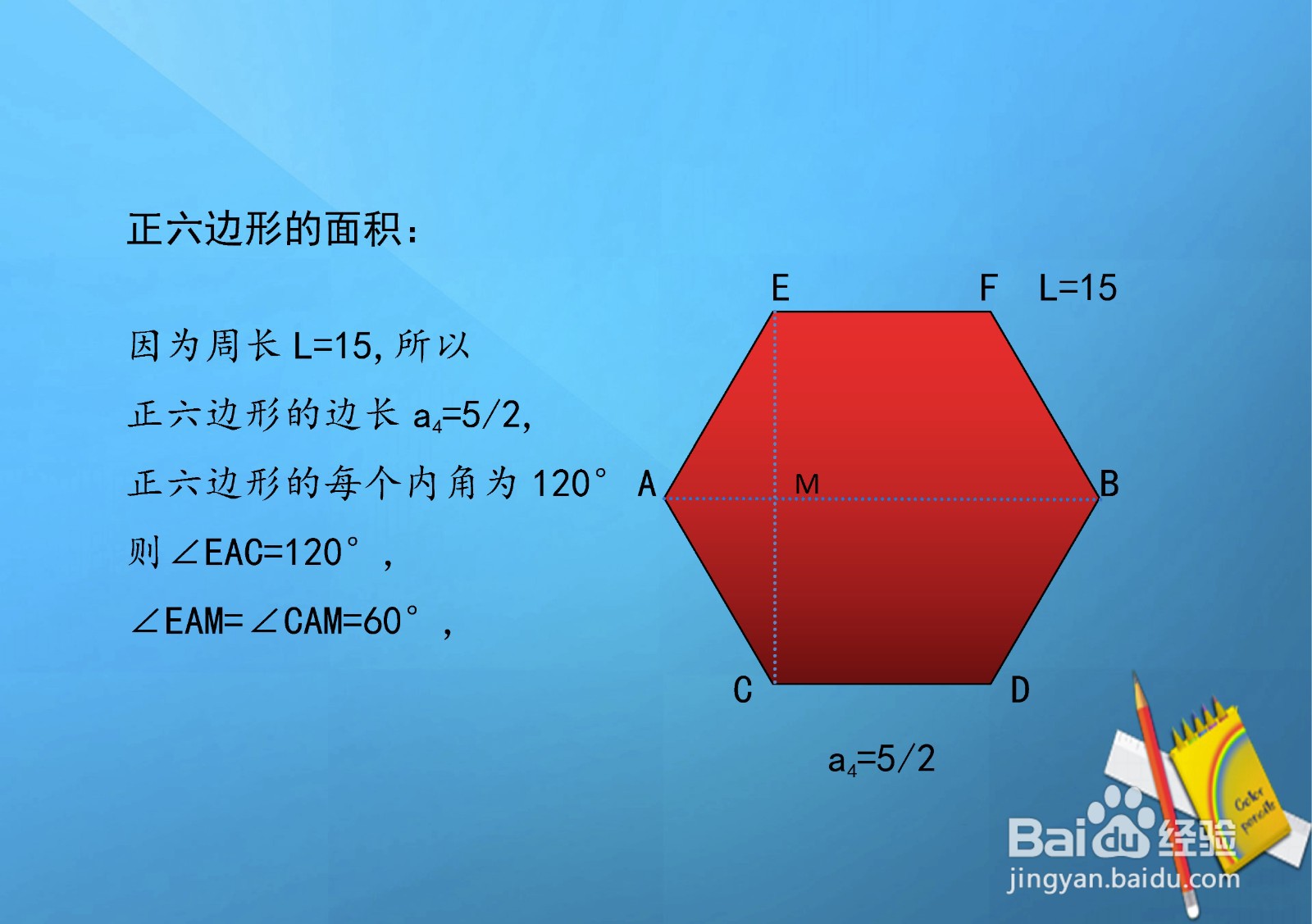
7、因为周长L=15,所以

正六边形的边长a4=5/2,                       

正六边形的每个内角为120° 

则∠EAC=120°,

∠EAM=∠CAM=60°

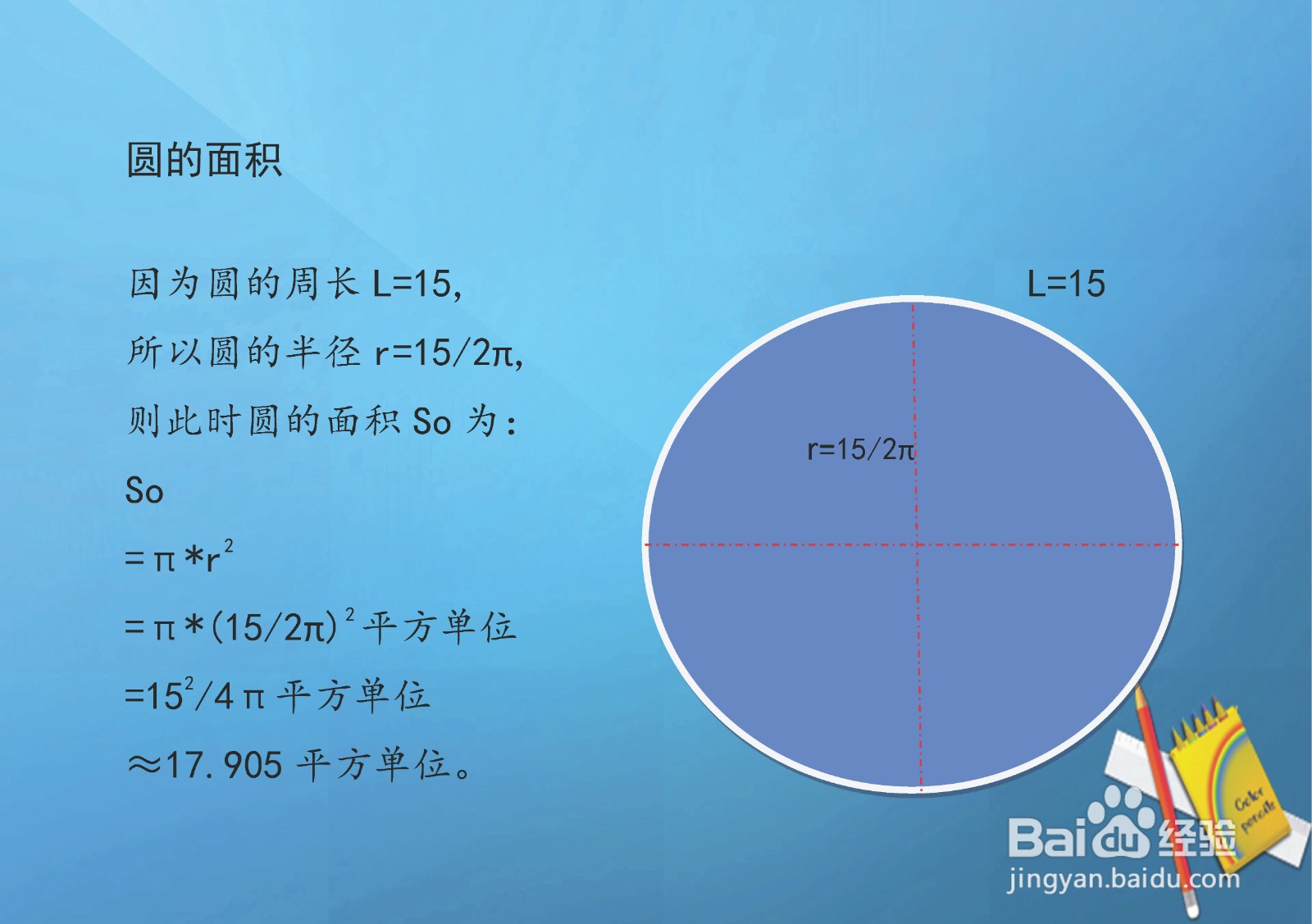
8、圆的周长面积与多边形的周长相等，进而得到圆的半径，通过圆的面积公式求得圆的面积。