证明函数单调性的方法

1、一、函数单调性定义

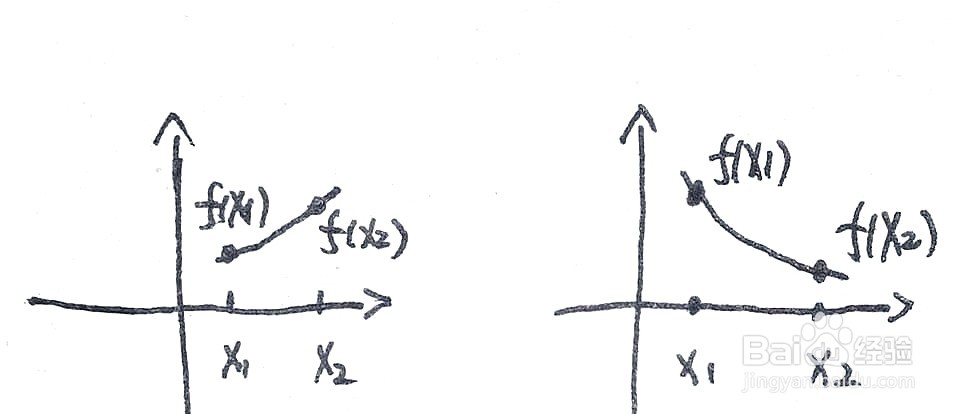
根据定义，要判断函数单调性，需要有两个点x1，x2，这两个点存在的区间包含于连续函数f(x)的定义域内，将这两个点带入函数f(x），比较得到的两个函数值f(x1)，f(x2)，如果x1<x2，且f(x1)<f(x2)，则函数单调增加，当x1<x2，且f(x1)>f(x2)，则函数单调减少

2、二、利用导数判断连续函数单调性

即题面要求连续函数单调性，但是给出的条件确是导数的时候，先确定区间（a，b）的连续函数在x0点处的导数f'(x0)≥0（或者≤0），其中使=成立的是有限个孤立点xk时，有f'(xk)=0，就可以判断出连续函数f(x)在区间（a，b）内是单调增加（减少）的