怎么寻找初等几何变换的不动点？

1、直线按照给定的向量平移，变成一条平行线。

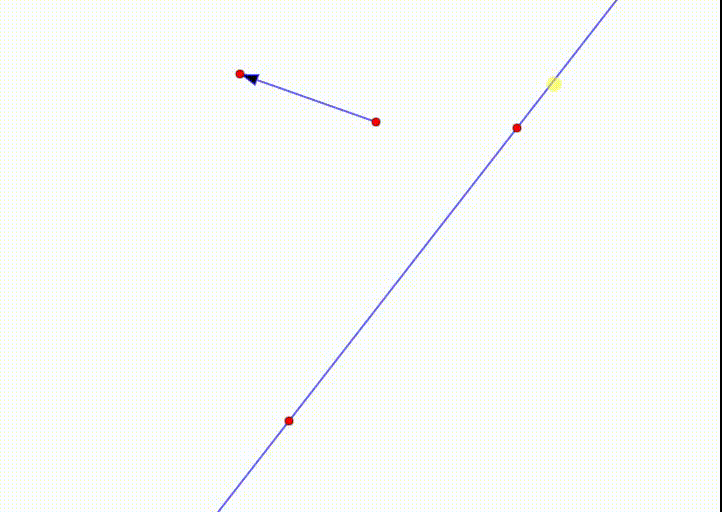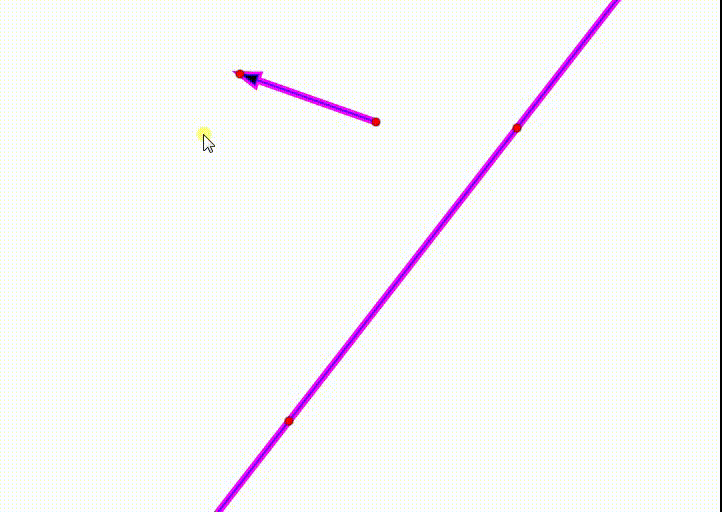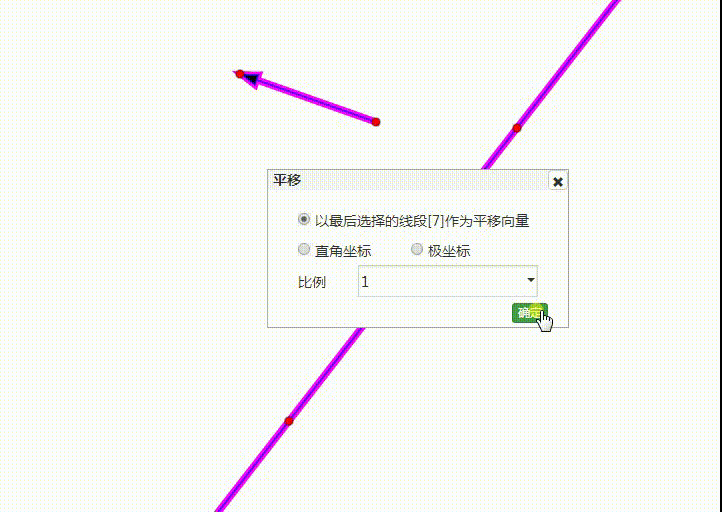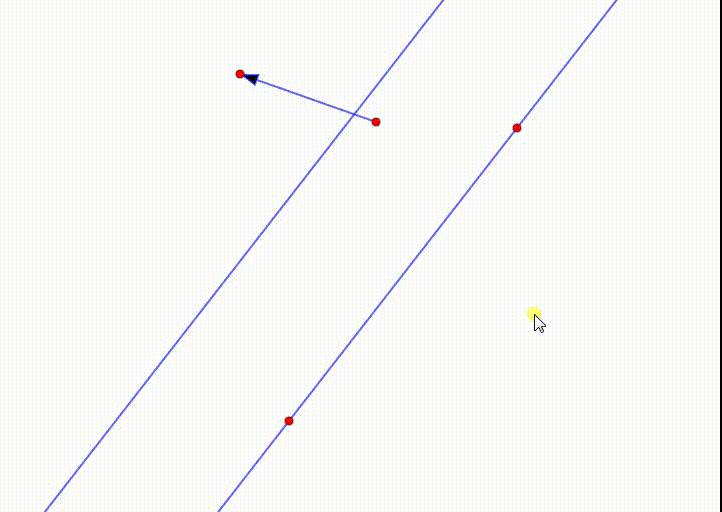
2、平面上每一个点，都发生了平移，所以，平移变换之下，不动点是不存在的。

除非平移向量是0向量。

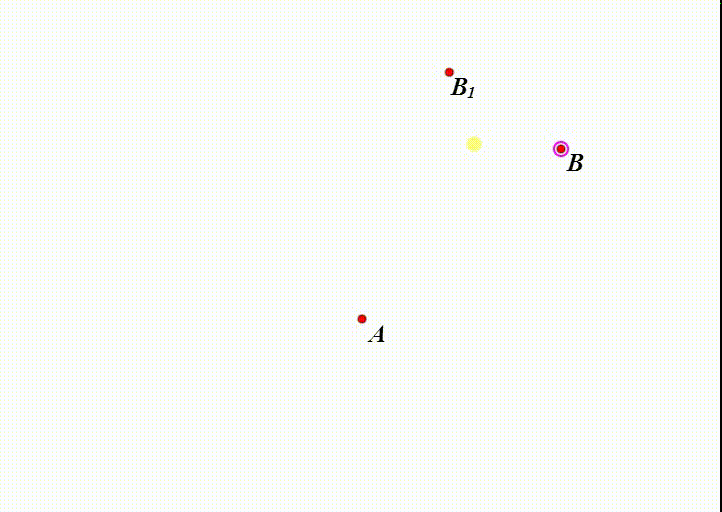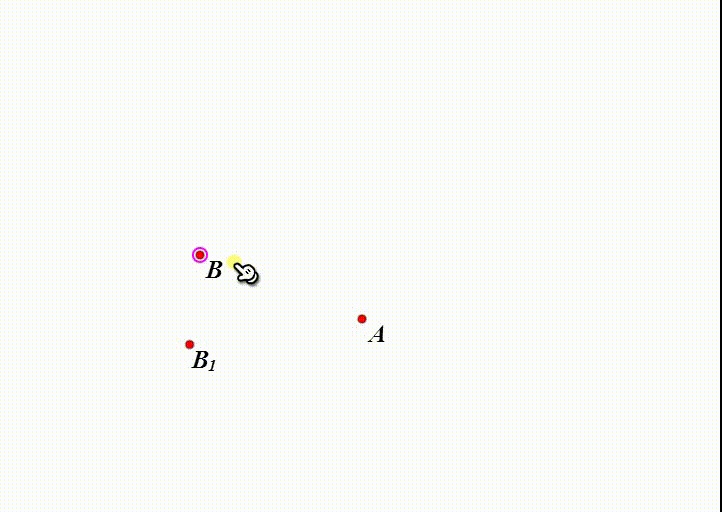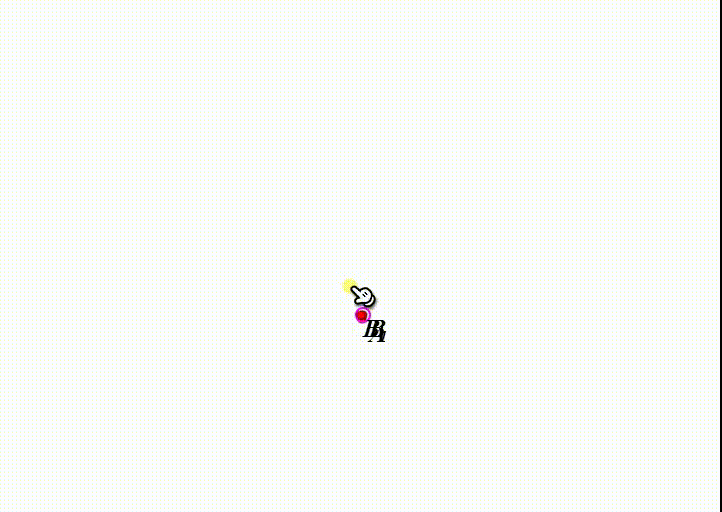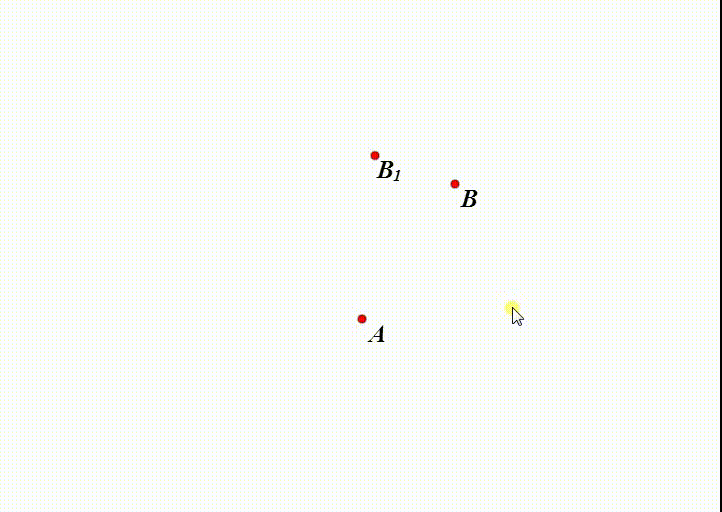
1、设A是旋转中心，B是平面上的自由点，B绕A旋转30°得到B1。

2、拖动B，B1也会随之改变。

当B与B1重合的时候，就得到不动点了。

显然，A作为旋转中心，就是不动点。

1、这里的反射，指的是图形关于直线的轴对称。

设AB是给定的直线，那么它把一侧的图形，变到另一侧。

2、因此，直线AB之外的点，一定不会是不动点。

而直线上的点都是不动点。

1、B向A缩小0.5，得到B1。

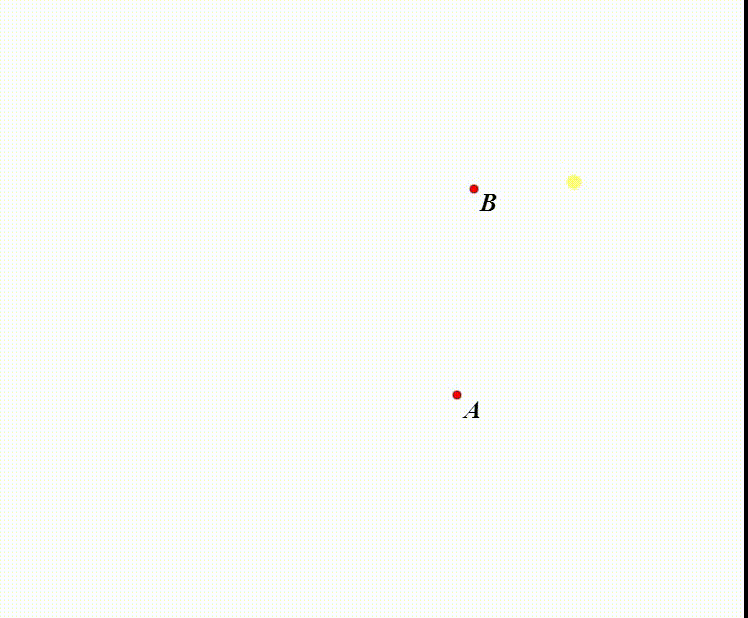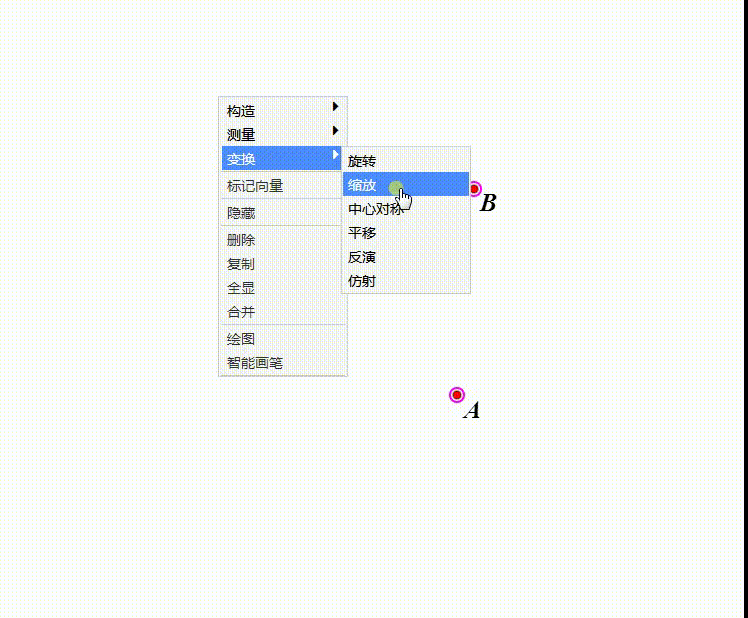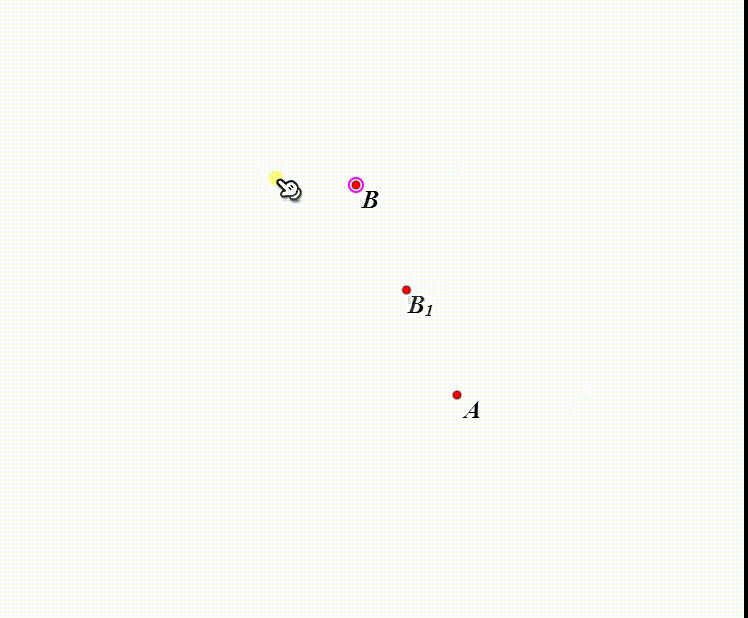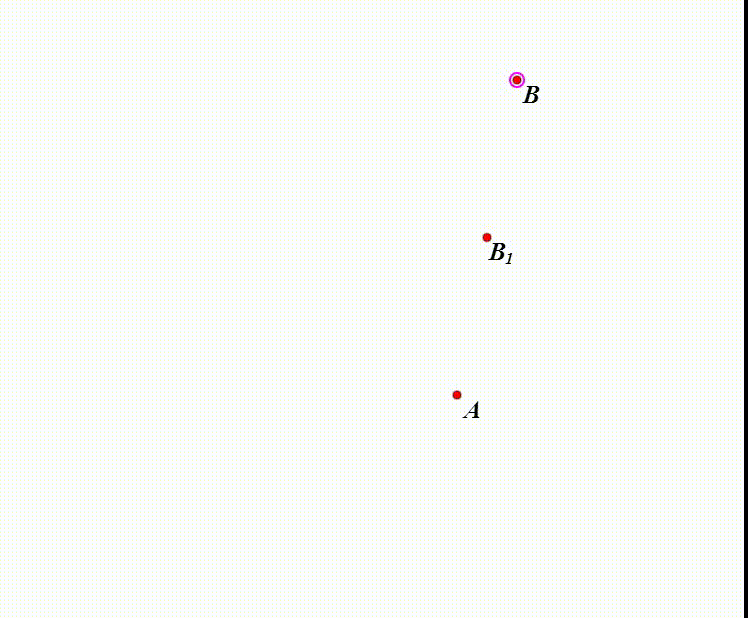
2、当B与B1重合的时候，B就与A重合了。

因此，A作为缩放中心，就是缩放的不动点。

1、假设A和B都是旋转中心；

C绕A旋转36°，得到C1；

C1绕B旋转54°，得到C2。

2、此时，由C到C2的变换，作用到整个平面上，会有不动点吗？

那就拖动C的位置，看看C与C2会不会重合。

你会发现，C与C2会重合。

3、但是：

C绕A旋转36°，得到C1；

C1绕B旋转-36°，得到C2。

那么，C和C2将永不能重合，也就表示没有不动点。