一个“探究性问题”的初步思考

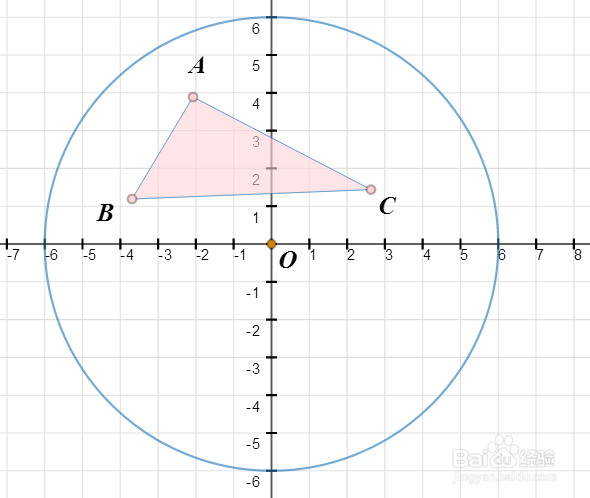
1、以O为圆心、画一个半径等于6的圆。

2、A、B、C是圆内任意的三个点；

构造△ABC（粉色）。

3、隐藏坐标系；

设D是△ABC内部的自由点；

E是△ABC边界上的自由点；

直线DE与△ABC的边界交于另一个点F；

直线DE与圆交于G、H。

4、隐藏圆和直线DE；

连接线段EF，做为折痕；

构造正方形GHG1H1；

选择正方形和△ABC，构造多边形的交，其实就是二者重合的区域，记为g，如下图紫色区域。

5、隐藏正方形；

构造g关于线段EF的轴对称图像h；

选择h和△ABC，构造多边形的交，记为u，见图中的绿色区域。

6、隐藏g和h以及点A、B、C；

分别测量△ABC和u的面积；

计算Su和S△ABC的比值，记为 t 。

7、D向右平移1个单位，得到X；

测量∠XDE的弧度 r，并把 r 属性改为“逆时针”，这样，r的取值范围就是0到2π。

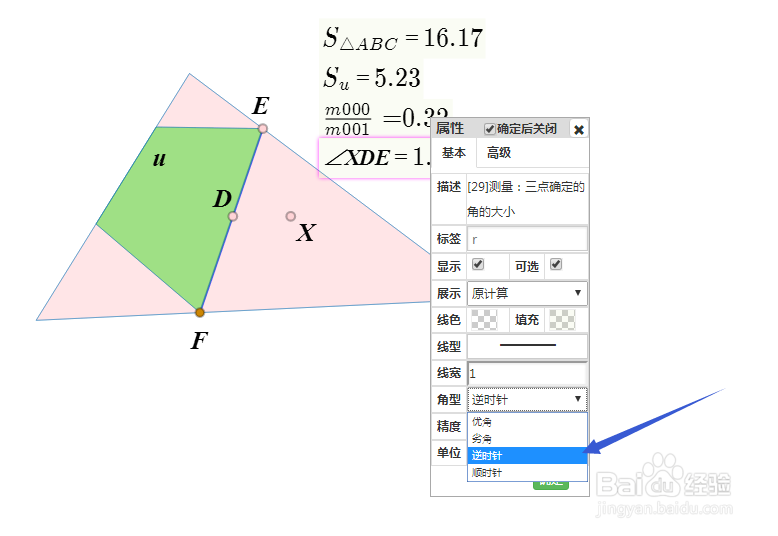
8、绘制直角坐标点U：横坐标是 r，纵坐标是 6*t ；

根据E来构造U的轨迹，如图中的绿色曲线。

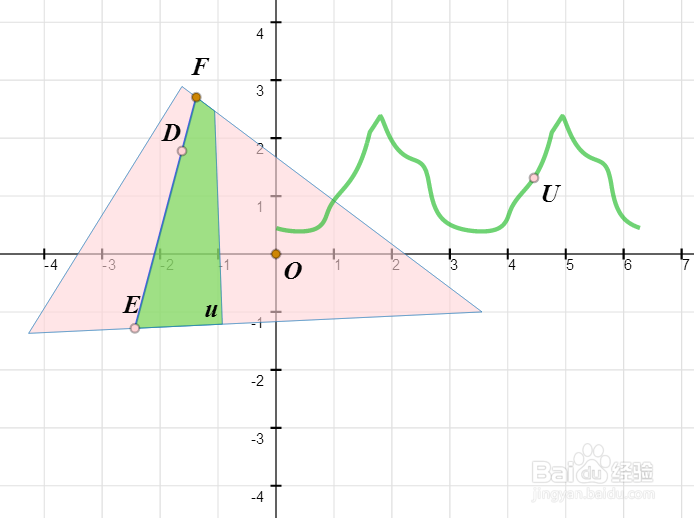
9、动点D，就是折痕的旋转中心。

当我们拖动D的时候，U轨迹的最高点就会发生变化；

如果我们能确定U轨迹的最高点的最大值，问题就得到了完美解决。

然而，暂时不能。