怎么查看和设定Mathematica函数的属性？

1、用Attributes可以查看内置函数的属性，如Plus函数，有六个属性：

{

 {Flat},

 {Listable},

 {NumericFunction},

 {OneIdentity},

 {Orderless},

 {Protected}

}

2、这些属性的含义如下图。

3、其中，比较有趣的是Listable和Orderless。

Listable的意思是，Plus可以分别作用于列表的每一个元素，而保持列表的结构不变。

这在图片处理的时候，有重要意义。

比如，给定一个3维列表list：

list = {{{9, 9, 5}, {4, 3, 5}, {5, 7, 0}, {7, 7, 5}, {7, 7, 5}, {2, 9,3}}, {{6, 1, 0}, {5, 2,  6}, {6, 9, 5}, {6, 5, 5}, {5, 9, 9}, {6,2, 3}}, {{6, 4, 8}, {4, 6, 2}, {8, 8, 6}, {8, 6, 9},  {5, 8, 9}, {4, 1, 4}}, {{0, 3, 0}, {5, 2, 2}, {7, 0, 5}, {4, 1, 6}, {6, 8, 2}, {4, 3, 5}}, {{7,  0, 1}, {0, 8, 5}, {4, 9, 1}, {5, 5, 2}, {4, 4, 6}, {6, 5, 4}}};

这个列表的结构是5*6*3，对应一个5*6的3通道图像。

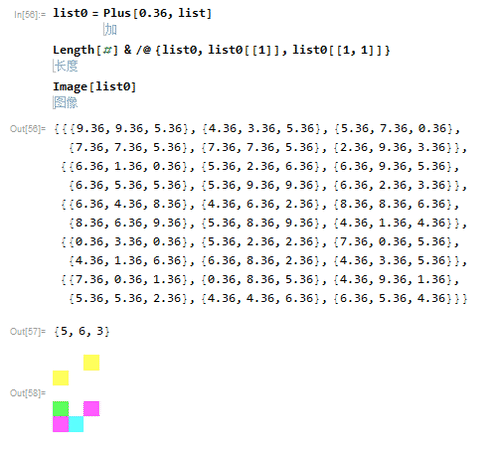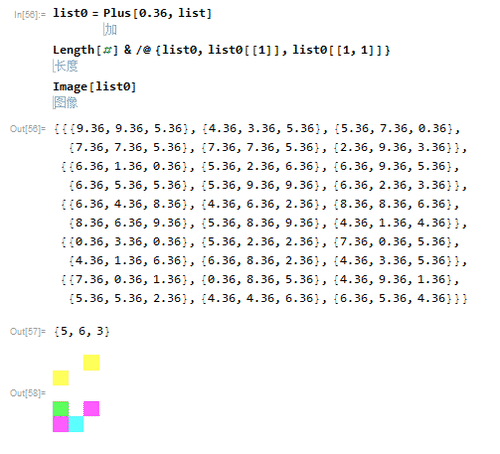
4、要想对list里面的每个数字，都加上0.6，就可以使用Plus：

list0=0.6+list

可以验证，list0确实是5*6*3的列表：

Length[#] & /@ {list0, list0[[1]], list0[[1, 1]]}

而对应的图像，大小完全一样，只有颜色变了。

5、Orderless是可交换的意思，就是说，加法满足交换率。

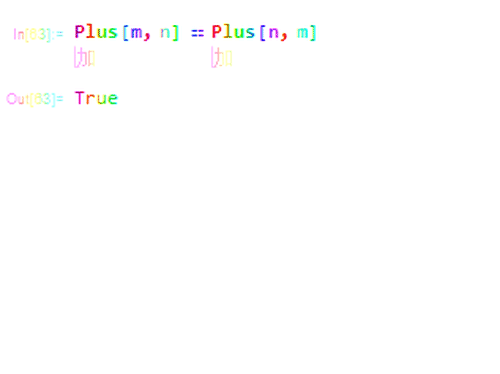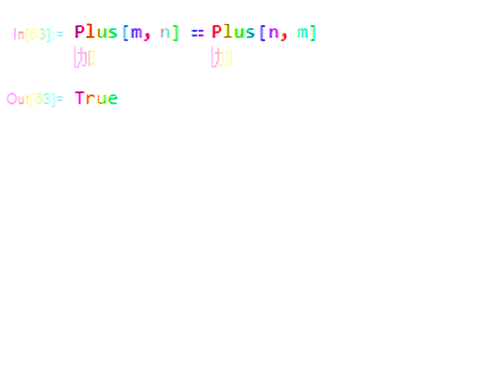
6、而减法只有三个属性：

Attributes[Subtract] // Column

容易验证，减法不满足交换律。

1、先自定义一个函数：

f[x_] := If[x >= 0.5, x^2, x^3]

此时，可以验证，自定义函数f没有任何特定属性：

Attributes[f]

2、然而，我想用这个自定义函数来处理图像，希望f具有listable属性，就需要指定一下：

Attributes[f] = {Listable}

3、此时给定一幅图片，如下图。

4、把上图变成图片数据data，再用f来作用于data的每一个元素，得到新的图片数据，转化为图片，结果如下。

5、实际代码如下图。