【微分几何】圆锥面上的曲线

1、圆锥面的参数方程可以是：

f[u_] := 2 u;

r[{u_, v_}] := {u Cos[v], u Sin[v], f[u]}

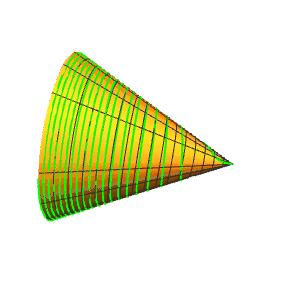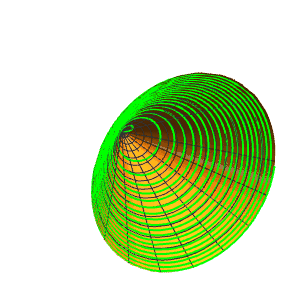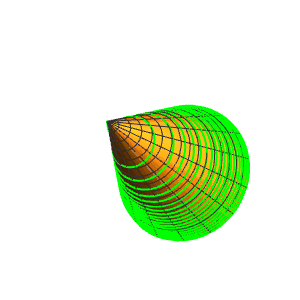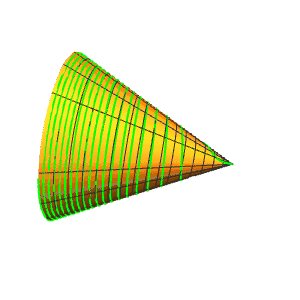
2、在圆锥面上画一条曲线r[{u, 6 u}]。

这可以视为一种螺旋线。

3、让螺旋线的密度变大。

r[{u, 16 u}]

4、密度渐变的螺旋线：

r[{u, u^2.6}]。

5、正弦曲线r[{u, Sin[6 u]/3}]。

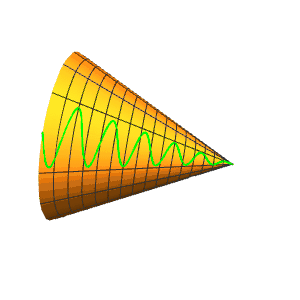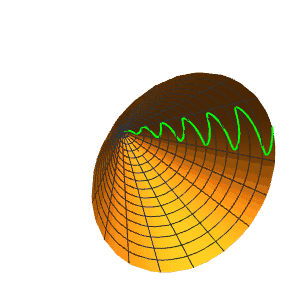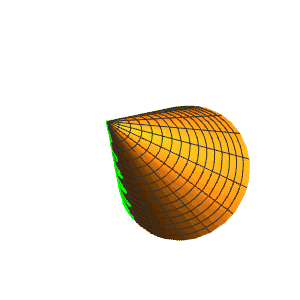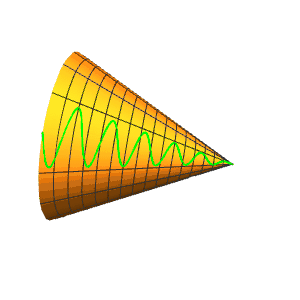
6、增加振幅，减少频率：

r[{u, Sin[u]*2 Pi}]

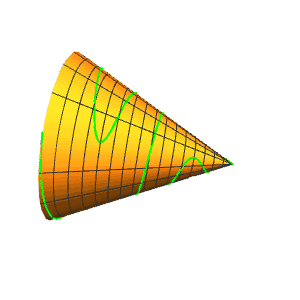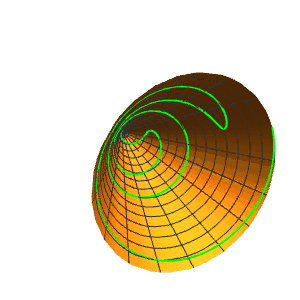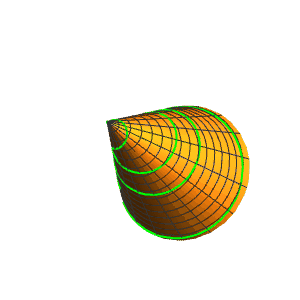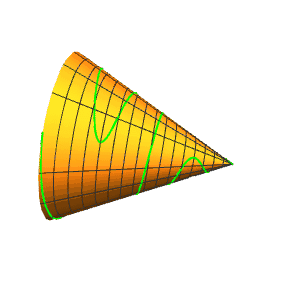
7、r[3 {Cos[u], Sin[u]}]，算作是锥面上的圆。

8、另一种形式的螺旋线：

r[u/18 {Cos[u], Sin[u]}]