【抽象代数】一个简单的三次代数数域的整基

1、由于F是Q的三次扩域，a是一个三次代数整数，那么，1,a,a^2就是线性无关的。

我们先求出a^2的不可约多项式。

2、假设a的绝对共轭数包括：

a,a',a''

那么，a^2的绝对共轭数也与之对应。

并且根据根与系数的关系，可以写出一组初等对称式。

3、下面，具体给出计算1,a,a^2的判别式的步骤。

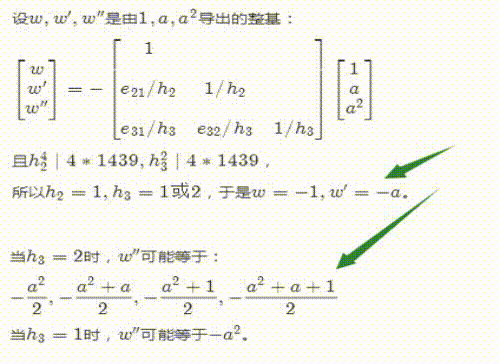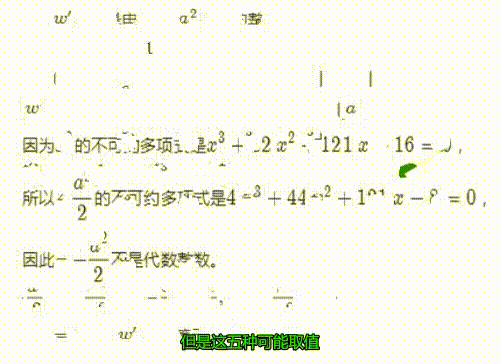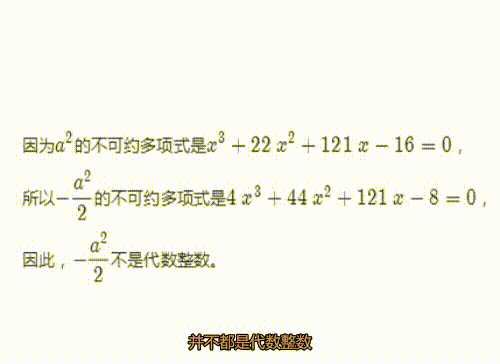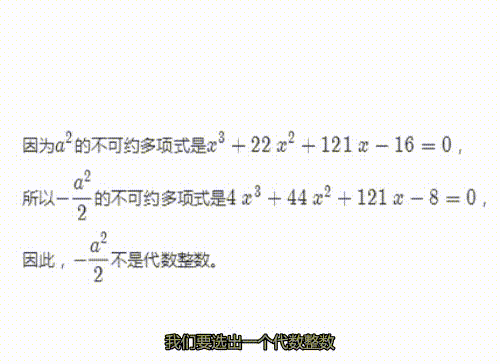
4、假设w,w',w''是由1,a,a^2导出的整基，那么我们可以写出w和w'，并确定出w''的可能的取值范围。

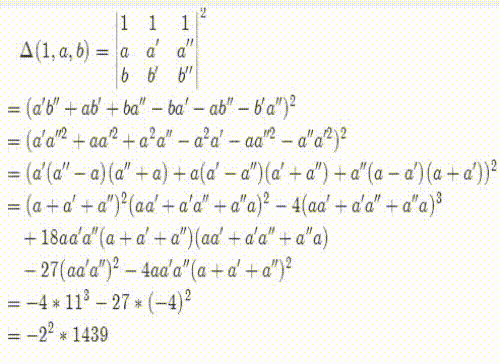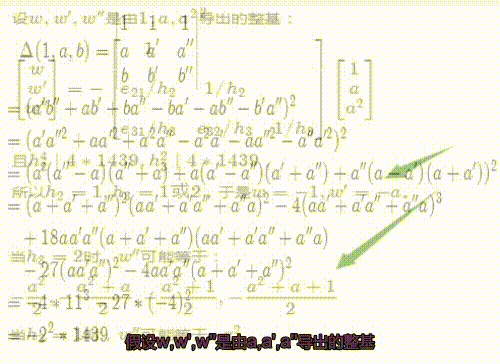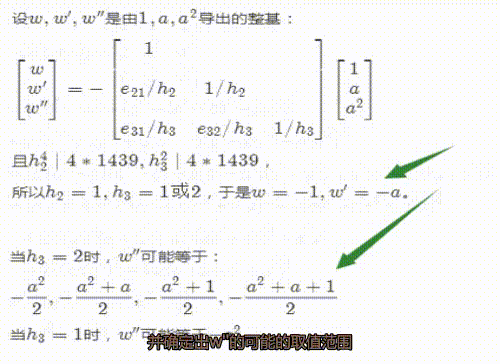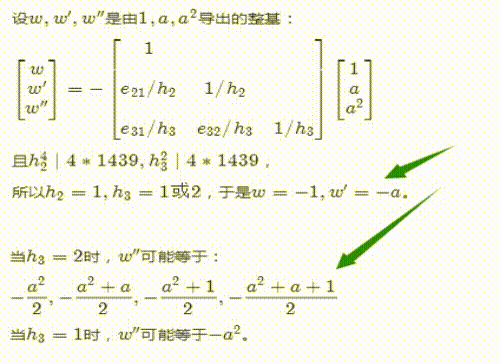
5、w''有五种可能，但是这五种可能取值，并不都是代数整数。

我们要选出一个代数整数。

先证明，a^2/2不是代数整数。

6、不过，第二种可能的取值，是一个代数整数。

因为它的不可约多项式是首一多项式。

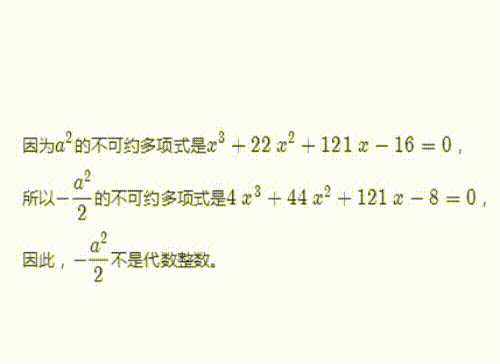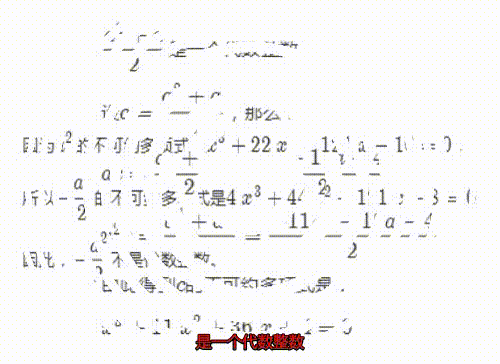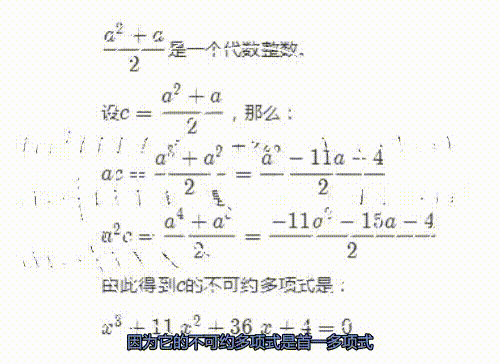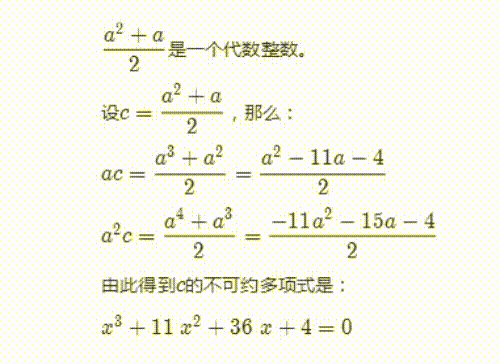
7、于是，可以写出F的一组整基，并算出F的基数。