视觉图像:Sobel算子及其实现
1、思想:
算子使用两个3*3的矩阵算子分别和原始图片作卷积,分别得到横向Gx和纵向Gy的梯度值,如果梯度值大于某一个阈值,则认为该点为边缘点;

2、矩阵转换:
事实上卷积矩阵也可以由两个一维矩阵卷积而成,在opencv源码中就是用两个一维矩阵卷积生成一个卷积矩阵:
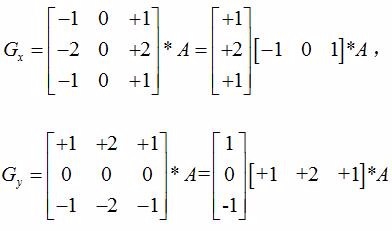
3、梯度值:
图像的梯度值由以下公式计算:
图像近似梯度值如下:
对于原始图像,P5的梯度值为:

4、OpenCV2410,sobel算子函数原型:
void Sobel(InputArray src,
OutputArray dst,
int ddepth,
int dx,
int dy,
int ksize=3,
double scale=1,
double delta=0,
int borderType=BORDER_DEFAULT )
函数参数解释:
InputArray src:输入的原图像,Mat类型
OutputArray dst:输出的边缘检测结果图像,Mat类型,大小与原图像相同。
int ddepth:输出图像的深度,针对不同的输入图像,输出目标图像有不同的深度,具体组合如下:
- 若src.depth() = CV_8U, 取ddepth =-1/CV_16S/CV_32F/CV_64F
- 若src.depth() = CV_16U/CV_16S, 取ddepth =-1/CV_32F/CV_64F
- 若src.depth() = CV_32F, 取ddepth =-1/CV_32F/CV_64F
- 若src.depth() = CV_64F, 取ddepth = -1/CV_64F
注:ddepth =-1时,代表输出图像与输入图像相同的深度。
int dx:int类型dx,x 方向上的差分阶数,1或0
int dy:int类型dy,y 方向上的差分阶数,1或0
其中,dx=1,dy=0,表示计算X方向的导数,检测出的是垂直方向上的边缘;
dx=0,dy=1,表示计算Y方向的导数,检测出的是水平方向上的边缘。
int ksize:为进行边缘检测时的模板大小为ksize*ksize,取值为1、3、5和7,其中默认值为3。特殊情况:ksize=1时,采用的模板为3*1或1*3。
当ksize=3时,Sobel内核可能产生比较明显的误差;
double scale:默认1。
double delta:默认0。
int borderType:默认值为BORDER_DEFAULT。
5、Sobel调用格式:
sobel算法代码实现过程为:
// 求 X方向梯度
Sobel( src_gray, grad_x, ddepth, 1, 0, 3, scale, delta, BORDER_DEFAULT );
// 求 Y方向梯度
Sobel( src_gray, grad_y, ddepth, 0, 1, 3, scale, delta, BORDER_DEFAULT );
convertScaleAbs( grad_x, abs_grad_x );
convertScaleAbs( grad_y, abs_grad_y );
addWeighted( dst_x, 0.5, dst_y, 0.5, 0, dst); //一种近似的估计

6、Sobel算子实现:
#include <opencv2\opencv.hpp>
using namespace std;
using namespace cv;
int main( int argc, char** argv )
{
Mat in_img = imread("raw.jpg",0);
if (!in_img.data)
{
return -1;
}
Mat out_img_dx = Mat::zeros(in_img.size(),CV_16SC1);
Mat out_img_dy = Mat::zeros(in_img.size(),CV_16SC1);
Mat out_img_dxy = Mat::zeros(in_img.size(),CV_16SC1);
GaussianBlur(in_img,in_img,Size(3,3),0);
unsigned char* p_data = (unsigned char*)in_img.data;
unsigned char* p_data_dx = (unsigned char*)out_img_dx.data;
unsigned char* p_data_dy = (unsigned char*)out_img_dy.data;
int step = in_img.step;
for (int i=1;i<in_img.rows-1;i++)
{
for (int j=1;j<in_img.cols-1;j++)
{
//通过指针遍历图像上每一个像素
p_data_dx[i*out_img_dx.step+j*(out_img_dx.step/in_img.step)]=abs(p_data[(i-1)*in_img.step+j+1]+2*p_data[i*in_img.step+j+1]+p_data[(i+1)*in_img.step+j+1]
-p_data[(i-1)*in_img.step+j-1]-2*p_data[i*in_img.step+j-1]-p_data[(i+1)*in_img.step+j-1]);
p_data_dy[i*out_img_dy.step+j*(out_img_dy.step/in_img.step)]=abs(p_data[i*in_img.step+j-1]+2*p_data[i*in_img.step+j]+p_data[i*in_img.step+j+1]
-p_data[(i+1)*in_img.step+j-1]-2*p_data[(i+1)*in_img.step+j]-p_data[(i+1)*in_img.step+j+1]);
}
}
addWeighted(out_img_dx,0.5,out_img_dy,0.5,0,out_img_dxy);
Mat img_dx,img_dy,img_dxy;
convertScaleAbs(out_img_dx,img_dx);
convertScaleAbs(out_img_dy,img_dy);
convertScaleAbs(out_img_dxy,img_dxy);
imshow("raw img",in_img);
imshow("x direction",img_dx);
imshow("y direction",img_dy);
imshow("xy direction",img_dxy);
Mat sobel_img;
Sobel(in_img,sobel_img,CV_8UC1,1,1,3);
imshow("opencv sobel",sobel_img);
waitKey( 0 );
return 0;
}



7、OpenCV内源码:
static void getSobelKernels( OutputArray _kx, OutputArray _ky, int dx, int dy, int _ksize, bool normalize, int ktype )
{
int i, j, ksizeX = _ksize, ksizeY = _ksize;
if( ksizeX == 1 && dx > 0 )
ksizeX = 3;
if( ksizeY == 1 && dy > 0 )
ksizeY = 3;
CV_Assert( ktype == CV_32F || ktype == CV_64F );
_kx.create(ksizeX, 1, ktype, -1, true);
_ky.create(ksizeY, 1, ktype, -1, true);
Mat kx = _kx.getMat();
Mat ky = _ky.getMat();
if( _ksize % 2 == 0 || _ksize > 31 )
CV_Error( CV_StsOutOfRange, "The kernel size must be odd and not larger than 31" );
std::vector<int> kerI(std::max(ksizeX, ksizeY) + 1);
CV_Assert( dx >= 0 && dy >= 0 && dx+dy > 0 );
for( int k = 0; k < 2; k++ )
{
Mat* kernel = k == 0 ? &kx : &ky;
int order = k == 0 ? dx : dy;
int ksize = k == 0 ? ksizeX : ksizeY;
CV_Assert( ksize > order );
if( ksize == 1 )
kerI[0] = 1;
else if( ksize == 3 )
{
if( order == 0 )
kerI[0] = 1, kerI[1] = 2, kerI[2] = 1;
else if( order == 1 )
kerI[0] = -1, kerI[1] = 0, kerI[2] = 1;
else
kerI[0] = 1, kerI[1] = -2, kerI[2] = 1;
}
else
{
int oldval, newval;
kerI[0] = 1;
for( i = 0; i < ksize; i++ )
kerI[i+1] = 0;
for( i = 0; i < ksize - order - 1; i++ )
{
oldval = kerI[0];
for( j = 1; j <= ksize; j++ )
{
newval = kerI[j]+kerI[j-1];
kerI[j-1] = oldval;
oldval = newval;
}
}
for( i = 0; i < order; i++ )
{
oldval = -kerI[0];
for( j = 1; j <= ksize; j++ )
{
newval = kerI[j-1] - kerI[j];
kerI[j-1] = oldval;
oldval = newval;
}
}
}
Mat temp(kernel->rows, kernel->cols, CV_32S, &kerI[0]);
double scale = !normalize ? 1. : 1./(1 << (ksize-order-1));
temp.convertTo(*kernel, ktype, scale);
}
}