视觉图像:熵计算-全局熵 vs 局部熵
1、信息熵:
信息论中信息熵概念为:求出任意一个离散信源的熵(平均自信息量)。
自信息是一个随机变量,它是指某一信源发出某一消息所含有的信息量。一条信息的信息量和它的不确定性有着直接的关系。所发出的消息不同,它们所含有的信息量也就不同。任何一个消息的自信息量都代表不了信源所包含的平均自信息量。不能作为整个信源的信息测度,因此定义自信息量的数学期望为信源的平均自信息量。
信息熵的意义:
信源的信息熵H是从整个信源的统计特性来考虑的。它是从平均意义上来表征信源的总体特性的。对于某特定的信源,其信息熵只有一个。不同的信源因统计特性不同,其熵也不同。信息熵一般用符号H表示,单位是比特。变量的不确定性越大,熵也就越大。

2、图像熵:是一种特征的统计形式,它反映了图像中平均信息量的多少。
一元灰度熵:一维熵
图像的一维熵表示图像中灰度分布的聚集特征所包含的信息量,令Pi表示图像中灰度值为i像素所占的比例,则定义灰度图像的一元灰度熵为:
其中Pi是某个灰度在该图像中出现的概率,可由灰度直方图获得。
图像的一维熵可以表示图像灰度分布的聚集特征;

3、二维熵:
图像的一维熵可以表示图像灰度分布的聚集特征,却不能反映图像灰度分布的空间特征;
为了表征这种空间特征,在一维熵的基础上引入能够反映灰度分布空间特征的特征量来组成图像的二维熵;
选择图像的邻域灰度均值作为灰度分布的空间特征量,与图像的像素灰度组成特征二元组,记为( i, j ),其中i 表示像素的灰度值(0 <= i <= 255),j 表示邻域灰度均值(0 <= j <= 255):
上式能反应某像素位置上的灰度值与其周围像素灰度分布的综合特征,其中f(i, j)为特征二元组(i, j)出现的频数,N 为图像的尺度,定义离散的图像二维熵为:
构造的图像二维熵可以在图像所包含信息量的前提下,突出反映图像中像素位置的灰度信息和像素邻域内灰度分布的综合特征。

4、熵函数:Entropy()和entropyFilt()
在Matlab中,熵运算函数有两个:Entropy()和entropyFilt();
Entropy()计算全局熵;
entropyFilt()计算局部熵;
Entropy(I)计算全局熵方法是:将灰度图I直方图化到0-255的bin中,L1规范化,再用 –sum(p*log2(p))来计算整理熵,
即,
Curhist = Hist(I, 0:255);
Curhist = curhist / sum(curhist);
E = -sum(curhist .* log2(curhist));
EntropyFilt(I)计算局部熵是:以像素点为中心的n*n(n=9)的区域进行熵计算,计算方法同上。该方法可以得到纹理图像;

5、matlab局部熵程序:-求纹理图像;
熵越大,无序程度越高;
图像中,根据像素点灰度分布的有序性,定义图像的局部熵,其反映了图像信息的丰富程度;
事件发生的概率越小,其包含的信息量就越大,其不确定性的程度就越高;
按照乘法的含义:事件的不确定性乘以其发生的概率,代表事物具体表现出来的不确定量。
clear all;close all;clc;
img1 = imread('raw.bmp');
img = rgb2gray(img1);%gray
[m n]=size(img);
w=4;%模板半径
imgn=zeros(m,n);%m*n维矩阵
for i=1+w:m-w
for j=1+w:n-w
Hist=zeros(1,256);%1*256维
for p=i-w:i+w%核大小
for q=j-w:j+w
Hist(img(p,q)+1)=Hist(img(p,q)+1)+1;%统计局部直方图
end
end
Hist=Hist/sum(Hist);
for k=1:256
if Hist(k)~=0
imgn(i,j)=imgn(i,j)+Hist(k)*log(1/Hist(k));%局部熵
end
end
end
end
imshow(imgn,[])
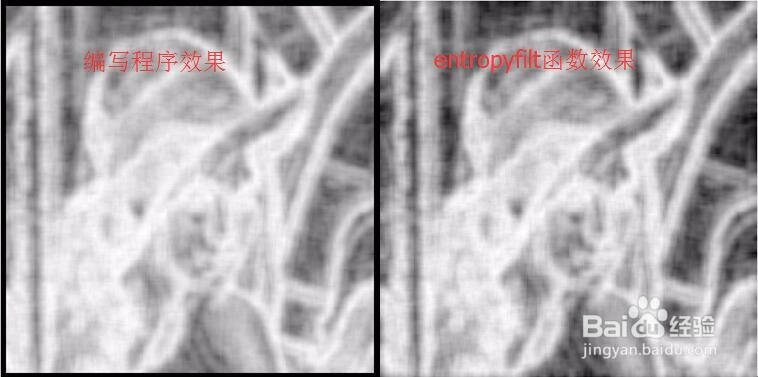
imgn=entropyfilt(img); %系统的局部熵函数entropyfilt
figure;
imshow(imgn,[]);

6、全局熵程序编写:求二维熵
%随机生成图像
A=floor(rand(8,8).*255);
[M,N]=size(A);
temp=zeros(1,256);
%对图像的灰度值在[0,255]上做统计
for m=1:M
for n=1:N
if A(m,n)==0;
i=1;
else
i=A(m,n);
end
temp(i)=temp(i)+1;
end
end
temp=temp./(M*N);
%由熵的定义做计算
result=0;
for i=1:length(temp)
if temp(i)==0;
result=result;
else
result=result-temp(i)*log2(temp(i));
end
end
7、// calculate entropy of an image
double Entropy(Mat img)
{
// 将输入的矩阵为图像
double temp[256];
// 清零
for(int i=0;i<256;i++)
{
temp[i] = 0.0;
}
// 计算每个像素的累积值
for(int m=0;m<img.rows;m++)
{// 有效访问行列的方式
const uchar* t = imgNaNr<uchar>(m);
for(int n=0;n<img.cols;n++)
{
int i = t[n];
temp[i] = temp[i]+1;
}
}
// 计算每个像素的概率
for(int i=0;i<256;i++)
{
temp[i] = temp[i]/(img.rows*img.cols);
}
double result = 0;
// 根据定义计算图像熵
for(int i =0;i<256;i++)
{
if(temp[i]==0.0)
result = result;
else
result = result-temp[i]*(log(temp[i])/log(2.0));
}
return result;
}