了解一下4阶对称群

1、四阶对称群S4有24个元素：

a = SymmetricGroup[4];

GroupOrder[a];

b = GroupElements[a]

其中的单位元是Cycles[{}]，表示不变。

2、对于S4里面的元素x，代表了一种轮换。

比如：

Permute[{p, q, r, s}, Cycles[{{3, 4}}]]

把{p, q, r, s}的第三个元素和第四个元素轮换一下。

3、Permute[{p, q, r, s}, Cycles[{{2, 3, 4}}]]

第四个元素跑到第二个位置上，第二个和第三个向右移动一个位置。

4、设x和y是S4的两个元素，那么xy表示先执行y，再执行x。

PermutationProduct[y,x]表示xy。

比如：

PermutationProduct[Cycles[{{2, 3, 4}}], Cycles[{{1, 2}}]]

Permute[{p, q, r, s}, %]

结果和下面的一样：

Permute[{p, q, r, s}, Cycles[{{2, 3, 4}}]];

Permute[%, Cycles[{{1, 2}}]]

5、产生S4的乘法表：

TableForm[GroupMultiplicationTable[a], TableHeadings -> Automatic]

6、查看S4里面，所有的二阶元素：

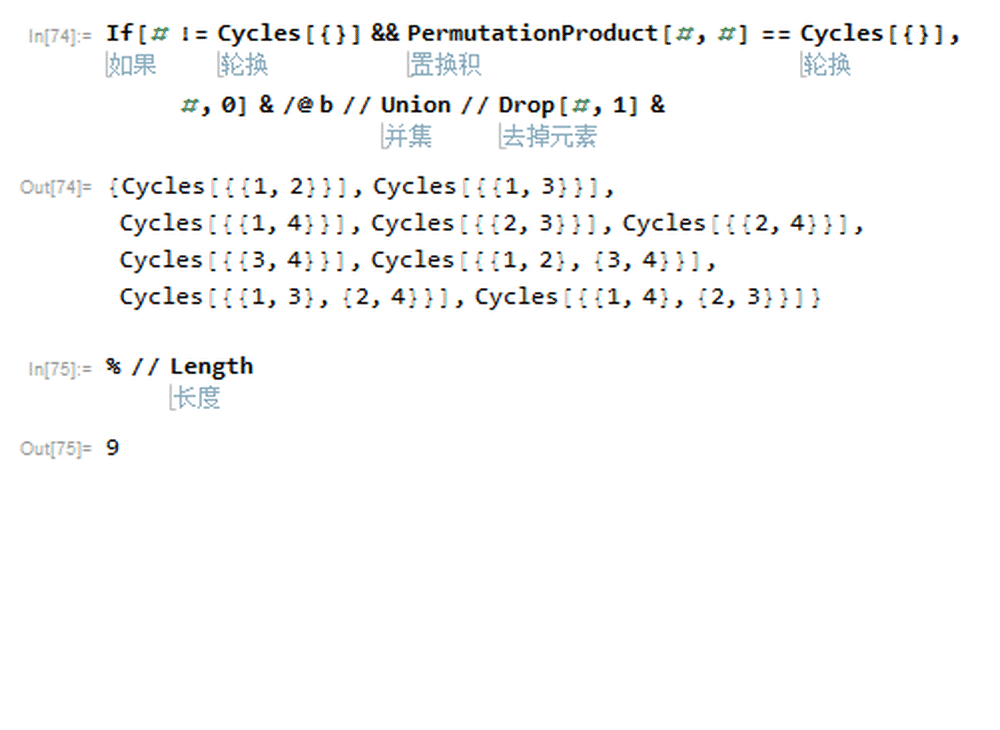
c=If[# != Cycles[{}] && PermutationProduct[#, #] == Cycles[{}], #, 

     0] & /@ b // Union // Drop[#, 1] &

一共有9个。

7、c加上单位元，能构成一个S4的子群吗？

看看它的乘法表：

c = If[PermutationProduct[#, #] == Cycles[{}], #, 0] & /@ b // Union //

   Drop[#, 1] &

TableForm[Table[PermutationProduct[m, n][[1]], {m, c}, {n, c}], 

 TableSpacing -> {5, 2}]