用Mathematica计算旋转矩阵

1、首先需要指出，二维空间里面，默认的旋转，都以原点为旋转中心。

平面上绕原点旋转u，对应的旋转矩阵是：

RotationMatrix[u]

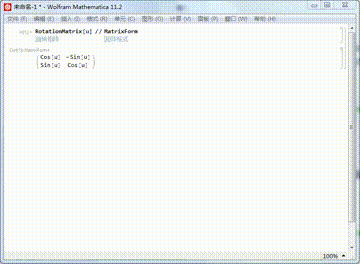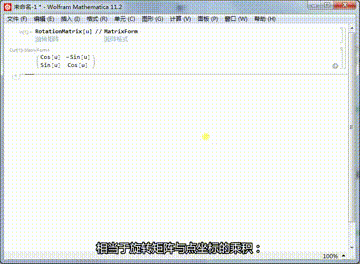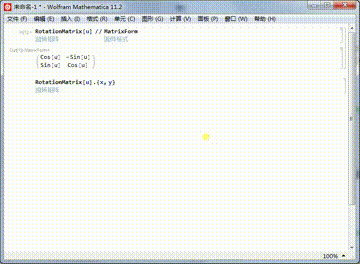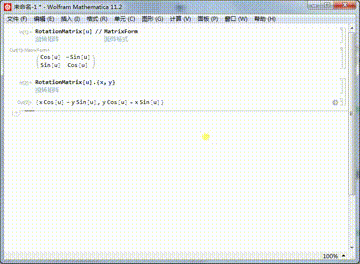
2、平面上某个点{x,y}，绕着原点旋转u，相当于旋转矩阵与点坐标的乘积：

RotationMatrix[u].{x,y}

3、三维空间里面，绕着x轴的旋转，可以表示为：

RotationMatrix[u, {1,0,0}]

注意，这时候，旋转中心已经不是原点了。

4、点{x,y,z}绕x轴旋转u，得到的点的坐标可以写成：

RotationMatrix[u, {1,0,0}].{x,y,z}

你会发现，旋转前后，点的x坐标不变。

5、设直线l经过原点，和点{x,y,z}，那么，绕直线l的旋转，就可以写成：

RotationMatrix[u, {x,y,z}]

6、上面这个矩阵很复杂，我们需要指定，x,y,z都是实数。

FullSimplify[

 Refine[RotationMatrix[u, {x, y, z}], 

   Element[{x, y, z}, Reals]] /. {Abs[x]^2 -> x^2, Abs[y]^2 -> y^2, 

   Abs[z]^2 -> z^2}]