MATLAB在控制工程中的几种建模方式
1、状态方程形式
在MATLAB中可以创建状态方程形如:,其中,x为状态变量,u和y分别为输入和输出变量。而A、B、C、D均为常数矩阵。
给出一个例子来说明函数ss的具体用法:
在MATLAB中输入:
A=[1 3;5 2];
B=[2;4];
C=[0 1];
D=[0];
sys_ss=ss(A,B,C,D)
运行之后,出现:
sys_ss =
a =
x1 x2
x1 1 3
x2 5 2
b =
u1
x1 2
x2 4
c =
x1 x2
y1 0 1
d =
u1
y1 0
Continuous-time state-space model.
其中,ss函数的输出量为状态方程中的常数矩阵,并提示此系统模型为连续的状态空间模型。
2、传递函数形式
当需要进行模型形式转换时,将其他模型形式转换为传递函数形式,则可以利用tf函数:
例:根据之前状态空间的输出结果,进行相应的转换,在MATLAB中输入:
sys_tf=tf(sys_ss)
则运行输出的结果为:
sys_tf =
4 s + 6
--------------
s^2 - 3 s - 13
Continuous-time transfer function.
从结果中可以看出,最终将状态方程转换成了传递函数模型,并提示为连续的传递函数。
3、零极点增益形式
有时会需要在传递函数的基础上,得到更加直观的系统表达,即一个系统的零极点,此时可以用到函数zpk,具体用法为:
在MATLAB中输入:
sys_zpk=zpk(sys_tf)
运行后出现结果:
sys_zpk =
4 (s+1.5)
-------------------
(s-5.405)(s+2.405)
Continuous-time zero/pole/gain model.
提示输出为连续的零极点模型。
4、频域响应数据形式
用Simulink对系统建立一个简单的模型,如图1所示:
图1 系统模型(零极点形式)
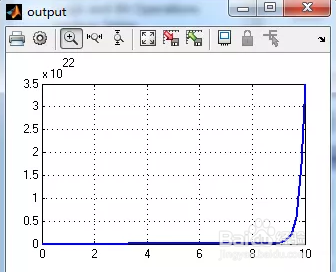
为了测得系统的频域响应,进而采样得到模型的信息,对系统输入一个正弦信号,并用示波器测量系统的响应输出,可以得到波形图如图4所示,其中示波器的具体参数配置如图2、图3所示。
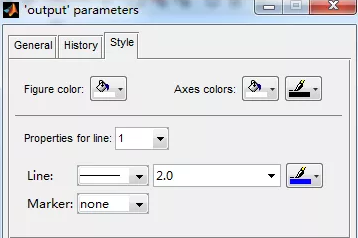
图2 示波器设置(设置绘图的图框及线型)
图3 示波器设置(将测量输出保存在变量output中)
图4 频率响应(针对频率为1rad/s的输入信号)
运行结束后,可以在MATLAB的workspace中找到变量output,它保存为一个结构变量,这个结构变量中又分为三个部分:表示时间的矩阵time、表示信号的结构变量signals、表示具体位置的字符串变量blockName。
PS:如果想在command窗口中绘制类似示波器测量输出的曲线图,可以输入以下命令:
>>plot(output.time,output.signals.values) %利用结构变量绘制图像
>> grid on
>> xlabel('time');
>> ylabel('output');
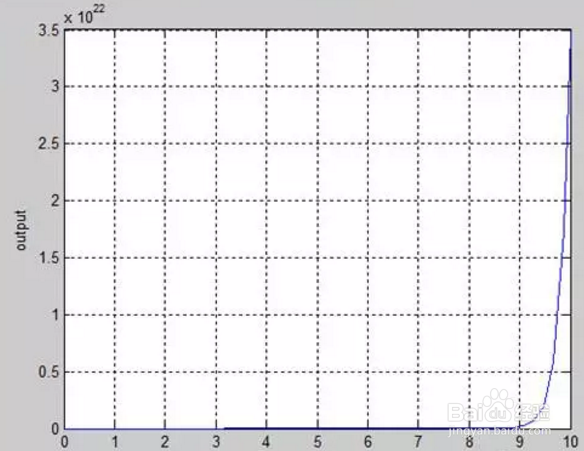
最后得到曲线如图5所示:
图5 频域响应形式曲线
从图中可以看出,曲线形状与示波器输出的曲线一样。