如何用KMP算法实现字符串匹配搜索(c++实现)
1、问题描述:
有两个字符串:
txt[] = "AABAACAADAABAABA"
pat[] = "AABA"
找到pat在txt当中的匹配位置。输出匹配后第一个字符的位置。
匹配位置为0,9, 12

2、我们将用KMP (Knuth Morris Pratt) 算法解决该问题。
该算法的时间复杂度为 O(n),在最坏的情况下。
相比于天真模式匹配方法(双重循环)的时间复杂度O(m(n-m+1)),该算法具有很大的优势。

3、KMP算法的基本思想:
即使当我们的模板检测不匹配时,我们也能够知道模板下一次匹配时主串的一些信息。
例子如下:
当“AAAA”匹配时,我们知道了主串的一些信息,下一步的匹配只需要检测模板的第四个元素是不是匹配。
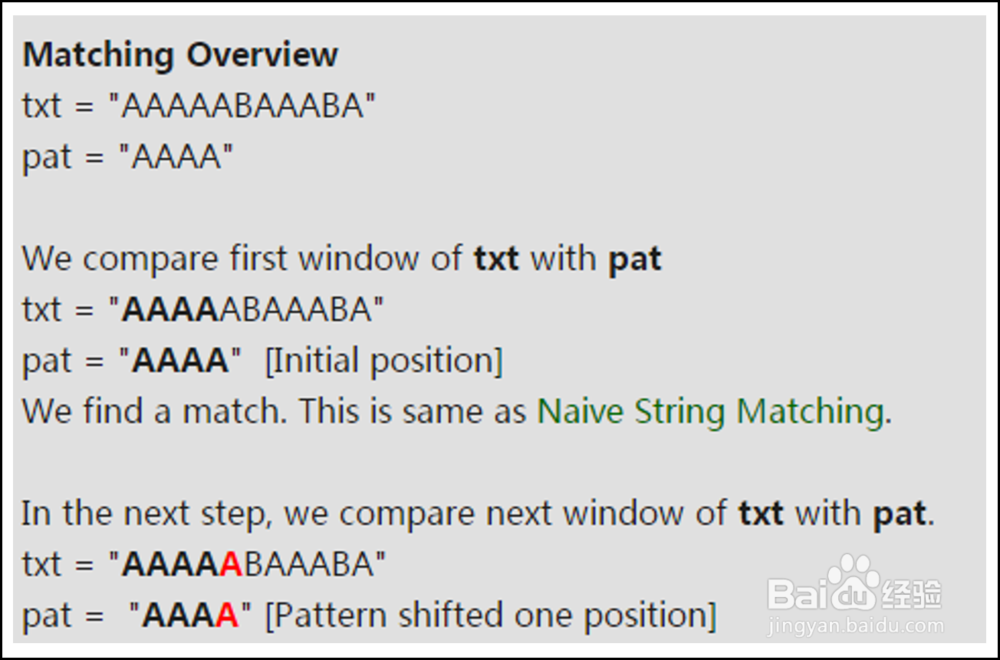
4、具体实现步骤:
对模板子串pat[]进行预处理,建立辅助的数组lps[],表示最长前缀大小。lps[i]暗示了多少个字符可以忽略
看下图常见的pat[]对应的lps[]。

5、那么如何如何计算lps[]数组呢,我们采用如下算法:
首先lps[0]永远等于0;
初始化len =0,i=0, len表示对应字符pat[i]对应的合适前缀长度。
增加i,即i=i+1;
如果pat[i]等pat[len]的话,len=len+1; lps[i]=len;
如果pat[i]不等于pat[len],len=lps[len-1],直到pat[i]等于pat[len],将len赋值给lps[i]。注意len减小到0之后不再减小



6、KMP搜索算法:
这一步建立在掌握了上述几步的基础上。
初始化i=0,j=0;
如果text[i]与pat[j]匹配,那么i++,j++;
如果j等于pat[]子串的长度时,及说明找到了匹配的子串。
如果text[i]与pat[j[不匹配时,或者j超粗了子串的长度时,令j=lps[j-1],重复上述操作




7、提供代码:
// C++ program for implementation of KMP pattern searching
// algorithm
#include <bits/stdc++.h>
void computeLPSArray(char* pat, int M, int* lps);
// Prints occurrences of txt[] in pat[]
void KMPSearch(char* pat, char* txt)
{
int M = strlen(pat);
int N = strlen(txt);
// create lps[] that will hold the longest prefix suffix
// values for pattern
int lps[M];
// Preprocess the pattern (calculate lps[] array)
computeLPSArray(pat, M, lps);
int i = 0; // index for txt[]
int j = 0; // index for pat[]
while (i < N) {
if (pat[j] == txt[i]) {
j++;
i++;
}
if (j == M) {
printf("Found pattern at index %d ", i - j);
j = lps[j - 1];
}
// mismatch after j matches
else if (i < N && pat[j] != txt[i]) {
// Do not match lps[0..lps[j-1]] characters,
// they will match anyway
if (j != 0)
j = lps[j - 1];
else
i = i + 1;
}
}
}
// Fills lps[] for given patttern pat[0..M-1]
void computeLPSArray(char* pat, int M, int* lps)
{
// length of the previous longest prefix suffix
int len = 0;
lps[0] = 0; // lps[0] is always 0
// the loop calculates lps[i] for i = 1 to M-1
int i = 1;
while (i < M) {
if (pat[i] == pat[len]) {
len++;
lps[i] = len;
i++;
}
else // (pat[i] != pat[len])
{
// This is tricky. Consider the example.
// AAACAAAA and i = 7. The idea is similar
// to search step.
if (len != 0) {
len = lps[len - 1];
// Also, note that we do not increment
// i here
}
else // if (len == 0)
{
lps[i] = 0;
i++;
}
}
}
}
// Driver program to test above function
int main()
{
char txt[] = "ABABDABACDABABCABAB";
char pat[] = "ABABCABAB";
KMPSearch(pat, txt);
return 0;
}


