用几何绘图软件绘制连杆曲线

1、        圆的连杆，其实就是固定一个端点的线段：

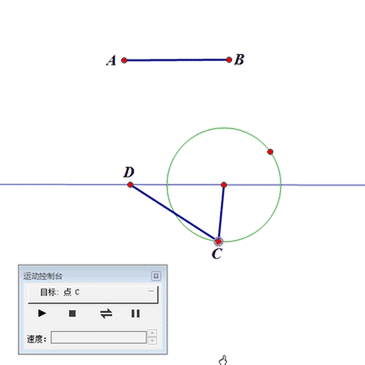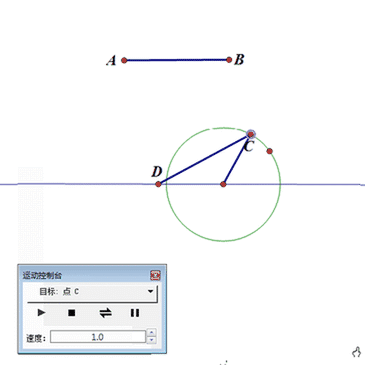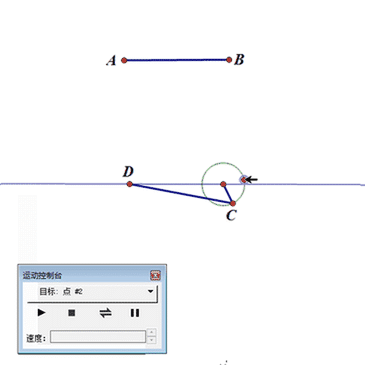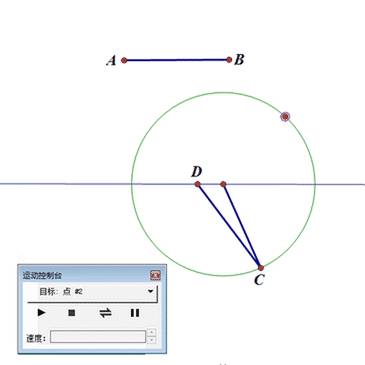
        先画一个圆O，保留圆的圆心O和控制点P；

        再构造圆上的动点C，圆外的固定线段AB（AB>圆O半径）和一条直线；

        以C为圆心、AB为半径作圆，与直线交于点D；

        选择点C，点击菜单里的“显示”——“生成点的动画”，点C就会带动线段AC运动，而且，点A是限制在直线上。

        此时，圆是动力输出中心，线段AC是传动机构。

2、        画椭圆的连杆是怎样构造的呢？我们有椭圆规，椭圆规就是利用连杆的原理来绘制曲线的一个工具。前面写过《怎么用几何画板构造椭圆规》，这里用另一种方法画一个椭圆规，步骤大体上相同，只是稍微简单点。

        以A为中心，作两条互相垂直的直线和一个圆；

        取圆上的动点B；

        作点B到两条直线的投影C、D（C、D分别位于两条直线上）；

        作直线CD；

        取直线CD上的自由点E，E的轨迹就是椭圆；

        连结线段AF（F为C、D的中点）。这就是椭圆规。

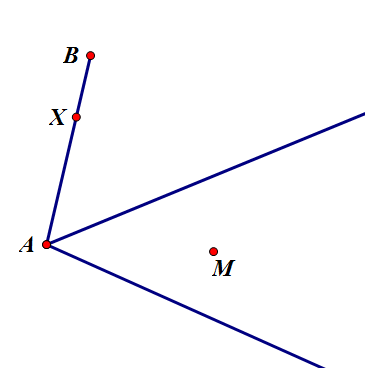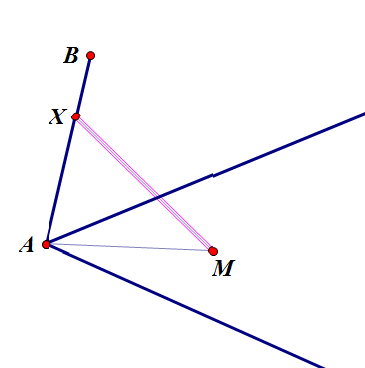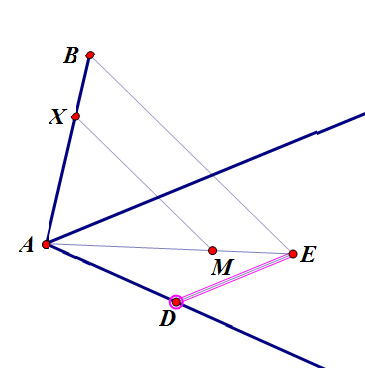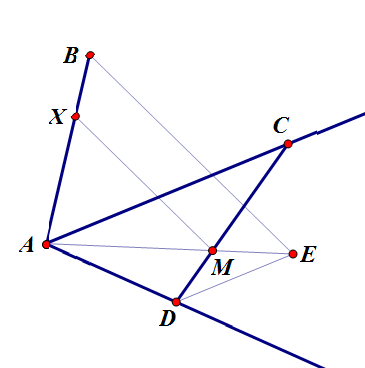
        在《怎么用几何画板构造椭圆规》里面曾给读者提了一个问题：两射线夹角内有一个点M，过M作线段与两射线交于C、D，且CM：MD=AX：XB，其中，ABX是事先给定的线段。下面解答一下这个问题：

        连结AM、XM；

        过B作XM的平行线，与直线AM交于E；

        过E作一条射线的平行线，与另一条射线交于D；

        连结DM，与对面射线交于C；

        此时必有CM：MD=AX：XB。

3、        绘制直线的连杆，第一次看到这个东西是在matrix67的博客里，其实这是利用了圆的反演变换原理实现的。

        给定A、B两点和线段GH、I J；

        以A为圆心、AB为半径作圆A，取圆A的自由点C；

        以B为圆心、I J为半径作圆B；

        以C为圆心、GH为半径作圆C；

        设圆B与圆C交于D、E；

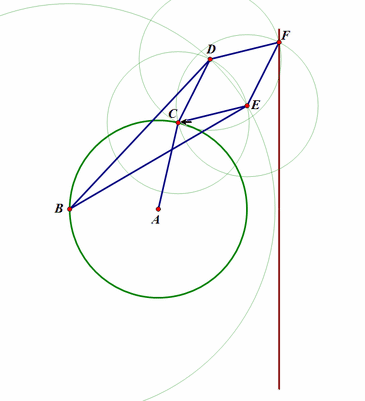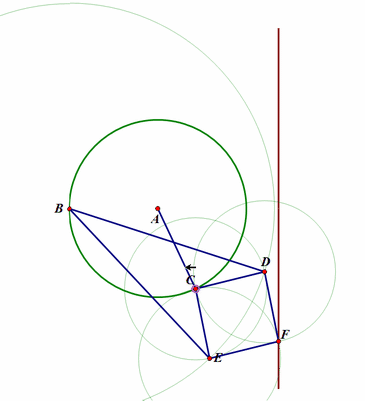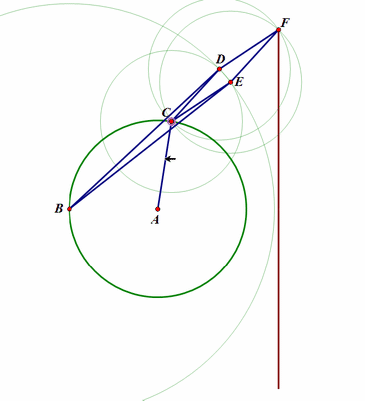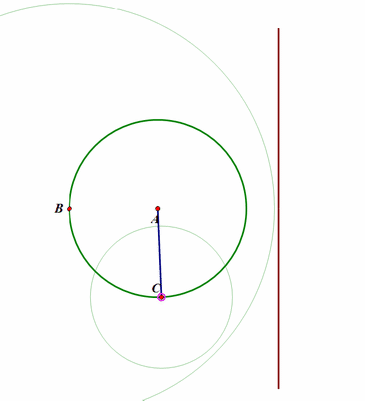
        分别以D、E为圆心，以GH为半径作圆，设两圆交于F；

        当C在圆上移动时，F的轨迹就是“直线”（实际上只是一条线段）；

        可以证明B、C、F三点共线。

        关于圆的反演变换，请参考《圆的反演变换及动态图演示》。你能够找到这个反演变换的反演中心和反演半径吗？

        当C的移动超过一定范围，图形就会消失一部分。所以，这个例子不成功，还需要修改。

4、        这里给出一个连杆系统，看看是否能够给出相应的连杆曲线的代数方程。

        以O为原点，ＡＢ为x轴；

        设OA=a，OB=b，AC=c，BC=d，AD=f；

        A点在时间t的坐标是：（cost,sint）；

        那么可以求出点D在时间t的参数坐标。D的参数坐标，正是轨迹曲线的参数方程，消去参数t，就能够变成代数方程。

        但由于具体的运算过程过于复杂，我试了一下就放下了。如果你有这个恒心，可以试试。

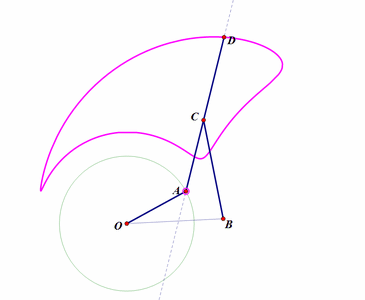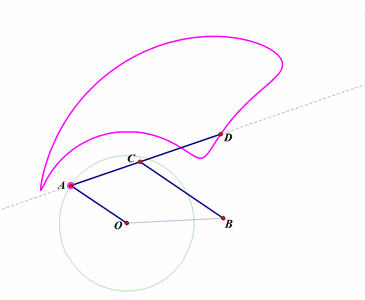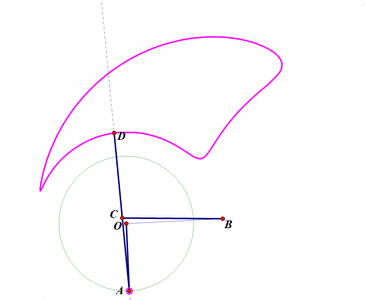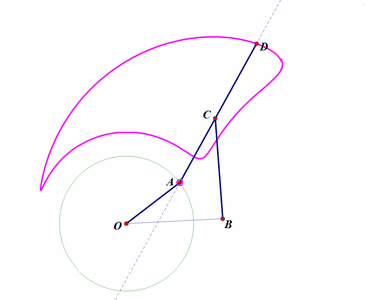
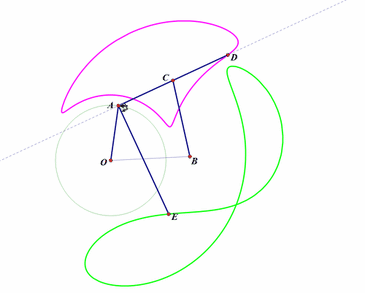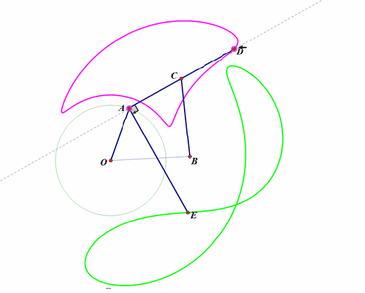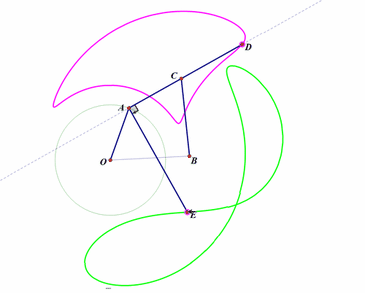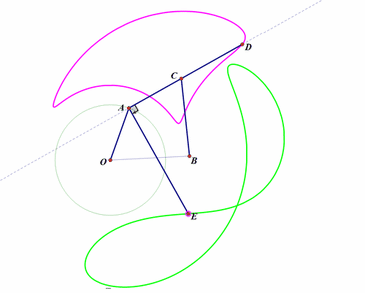
5、        再构造一个连杆系统。不同的点绘制出不同的连杆曲线，读者如果有兴趣，可以尝试着求出它们的参数方程和代数方程。如下图：

        固定两点O、B；

        构造连杆系统OACB（这里，OA、AC、CB的长度都是固定不变的）；

        D点位于直线AC上；

        E位于直线AC过A点的垂线上；

        当A绕点O转动，D的轨迹是粉红色曲线，E的轨迹是浅绿色曲线；

        改变D、E在直线上的位置，相应的轨迹也会随之改变。