相机标定：内外参数

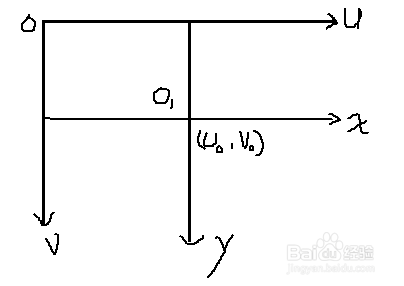
1、图像物理坐标系 转 图像像素坐标系

【注】：

图像像素坐标系o-uv，单位像素；

图像物理坐标系o1-xy，单位mm；

齐次矩阵转换关系：

其中，

u0,v0为图像像素坐标系中光轴投影坐标即主点坐标，

1/dx,1/dy分别为在x方向上每个像素的物理尺寸，在y方向上每个像素的物理尺寸，

gama为x,y不垂直时的扭曲系数，一般为0；。

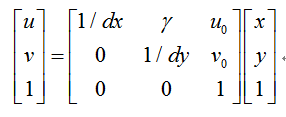
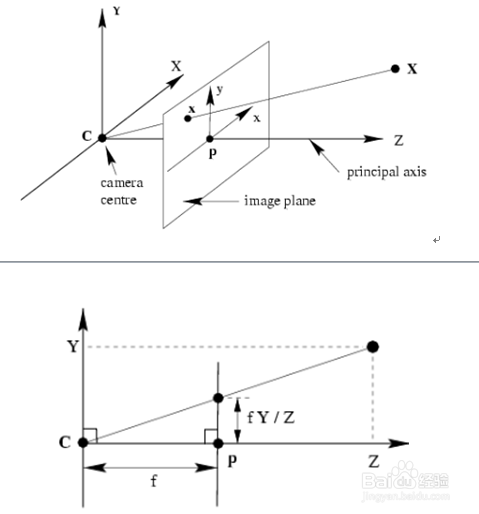
2、相机坐标系 转 图像物理坐标系

x,y为图像物理坐标系；

Xc,Yc,Zc为相机坐标系；

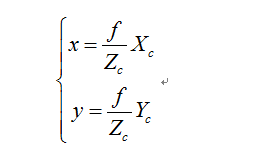
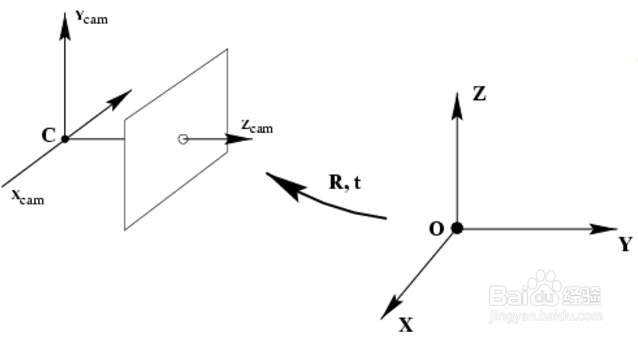
3、世界坐标系 转 相机坐标系

其中，R为旋转矩阵，T为平移向量。

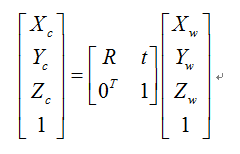
4、世界坐标系下，三维空间点投影像点，关系为：

公式2：

s为缩放因子

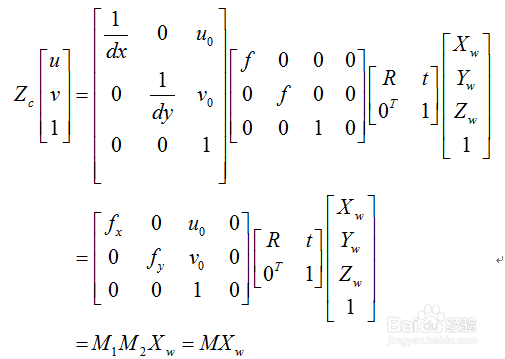
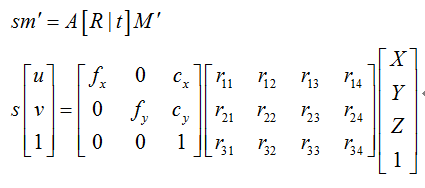
5、镜头畸变:

镜头畸变发生在成像过程中，即图像物理坐标系中。

畸变的产生：

由于理想的针孔模型，透过针孔的光线少导致相机曝光慢，因此在实际中，相机采用透镜成像模型，以使图像生成迅速，但代价就是引入了畸变。

有两种畸变对投影图像影响较大：径向畸变和切向畸变。

什么是径向畸变？

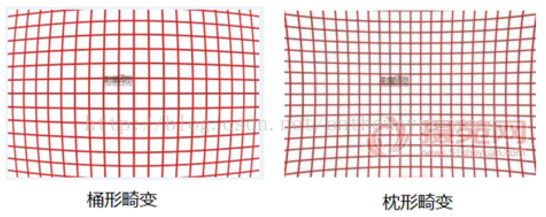
光线在远离透镜中心的地方比靠近透镜中心的地方更加弯曲，产生“筒形”或“鱼眼”现象，称为径向畸变。

一般，径向畸变在成像中心为0，越向边缘移动，畸变越严重。

径向畸变主要包含：筒形畸变和枕形畸变两种。

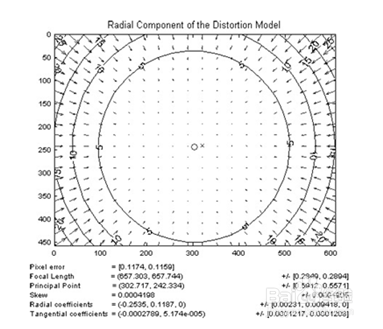
径向畸变可以由泰勒展开式校正。

径向畸变校正公式：

其中，(x,y)经透镜畸变后的坐标点，r为该点与成像中心的距离，(xcorrected,ycorrected)为畸变校正后的坐标点。

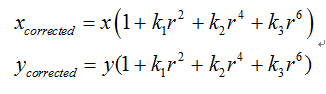
6、什么是切向畸变？

产生原因：当成像仪被贴在摄像机上时会存在误差，使透镜不完全平行图像平面。

现象：如果一个矩形被投影到成像仪上时，可能会变成一个梯形。

切向畸变校正公式：

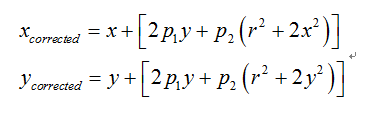
7、【注】：齐次坐标

定义：将一个n维向量用n+1维向量表示。

目的：合并矩阵运算中的乘法和加法，以最后形式为x=P*X结束。

即采用矩阵运算以使二维、三维甚至高维空间中的一个点集从一个坐标系到另一坐标系的有效方法。