【平面几何】角平分线分线段成比例证明方法

1、一方面，注意到△ABD和△ACD有相同的高AH，因此，两个三角形的面积之比等于BD:CD。

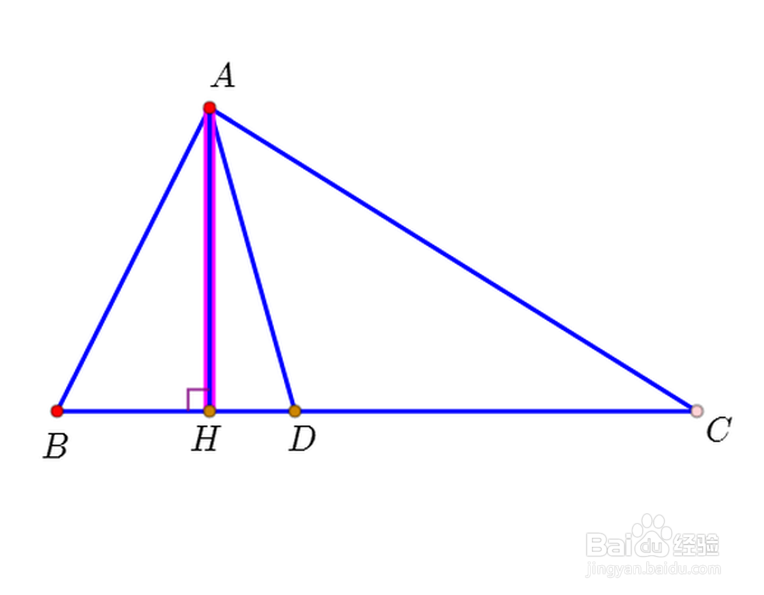
2、另一方面，点D到AB、AC的距离相等，因此，两个三角形的面积之比又等于AB:AC。

如此一来，定理得证。

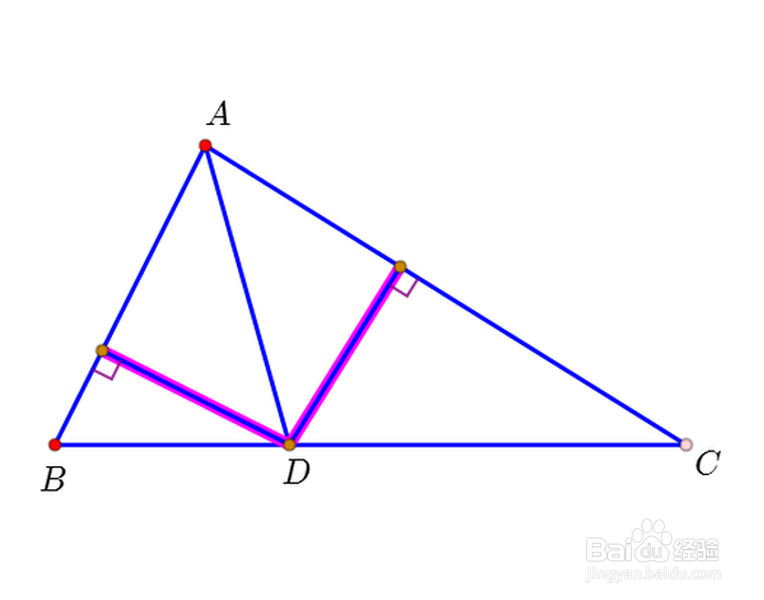
1、作B、C在直线AD上的垂足M、N，因为AD平分∠BAC，所以有：

AB:AC=BM:CN。

注意图中的相似三角形。

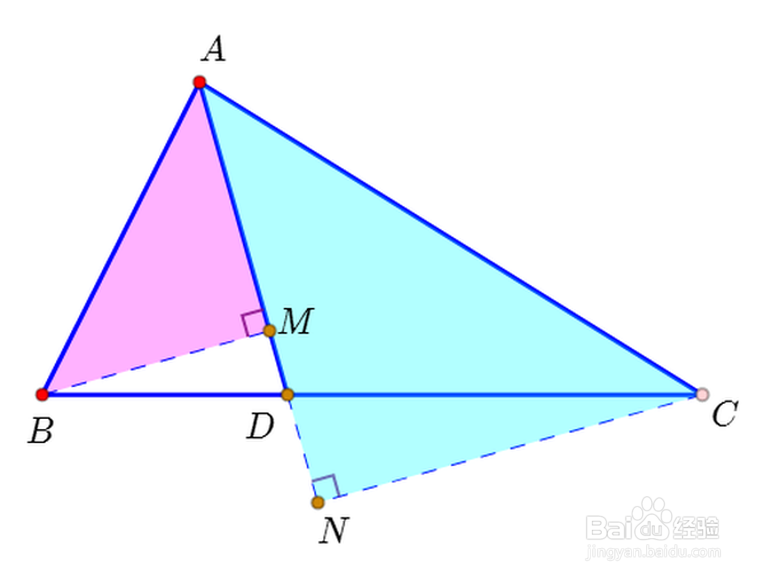
2、因为BM//CN，所以有：

BM:CN=BD:CD。

所以定理成立。

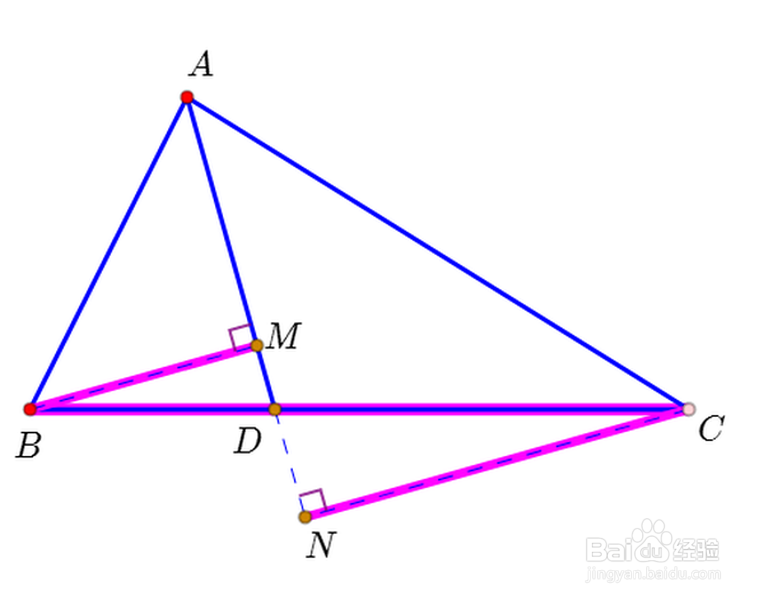
1、过点B作AD的平行线，与直线AC交于X点。

因为AD是∠BAC的平分线，所以∠AXB=∠ABX，所以AX=AB。

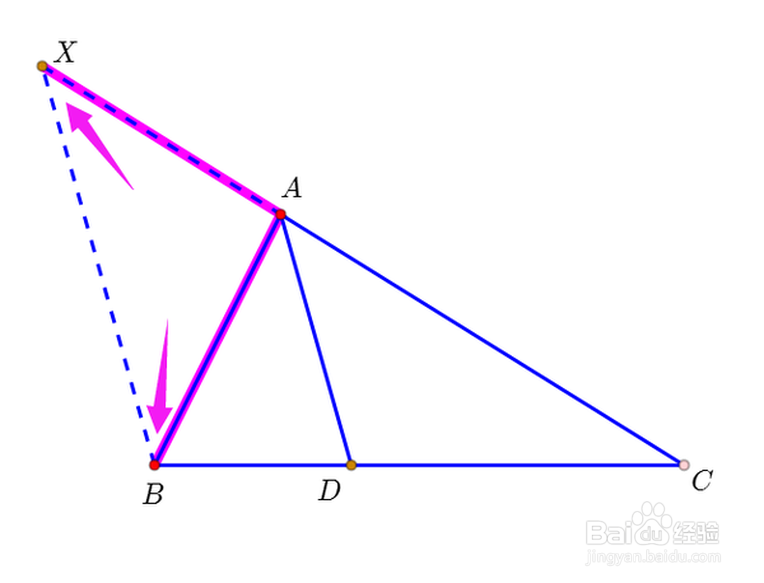
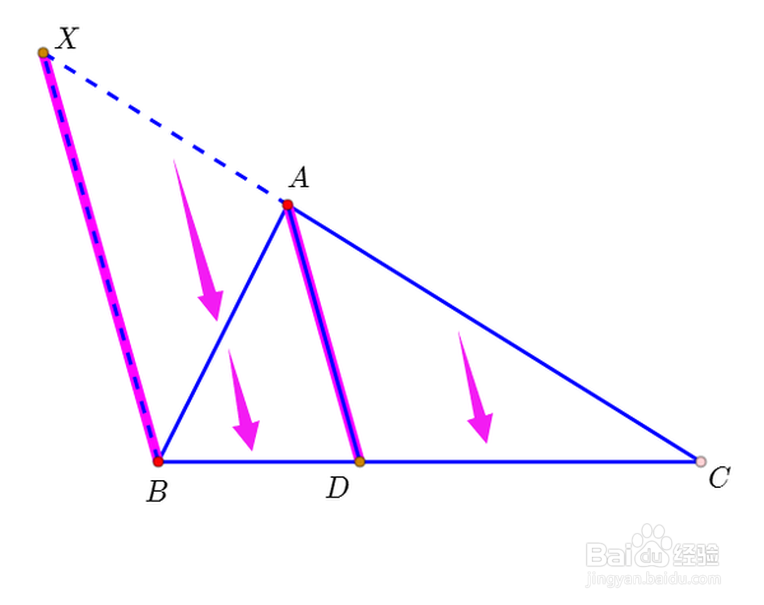
2、因为BX//AD，所以，AX:AC=BD:CD，所以AB:AC=BD:CD。

用AB替换AX。