复变函数问题一则

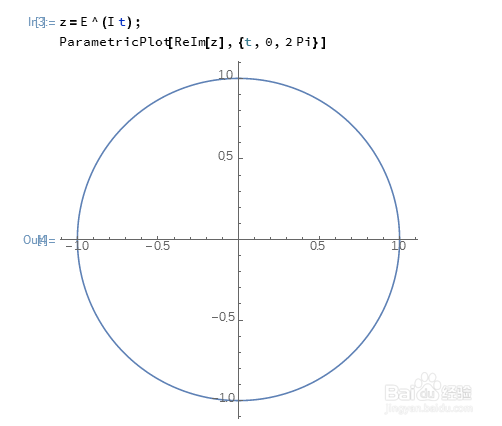
1、首先，复数z的模长等于1，那么，z在复平面上的轨迹曲线就是单位圆。设z=E^(I t)，t的取值范围为0到2*π。这样，所有满足要求的z都囊括在内了。

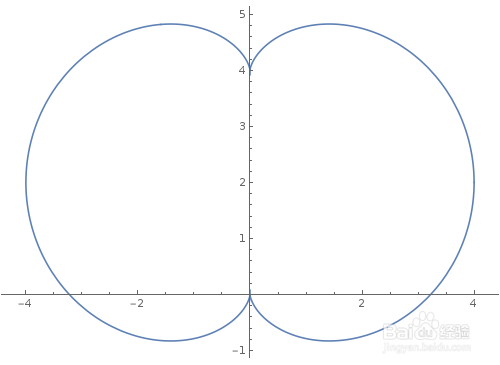
2、看看z^3+3*z+2*I在复平面上的图形，是什么样子滴！

用ComplexExpand展开z^3+3*z+2*I，然后就可以看到图形对应的参数方程（分别是实部和虚部）。曲线上，离原点最远的点，就是所有表达式的模长最大值。

3、直接用Norm求表达式的模长,是不行的。因为Mathematica把t视为全体复数了。

大家可能要问，为什么作图的时候，不会发生这个情况？

其实，作图的时候，绘图范围已经把t限制在实数范围之里了。

可是，即使在Norm前面，我们限定t>0，也无济于事，我真是无语了。

同样的，ReIm也无力。

4、所以，我用Part强行把实部和虚部分开。然后在计算模长。

令a=z^3+3 z+ 2 I;

b=ComplexExpand[z^3+3 z+ 2 I]

运行结果是：3Cos[t]+Cos[3t]+I*(2+3Sin[t]+Sin[3t])

那么，a的实部和虚部就可以求出来。

注意，最后那一步化简，用的是模长^2。

知道了模长表达式，在用Maximize，就可以求出最大值。

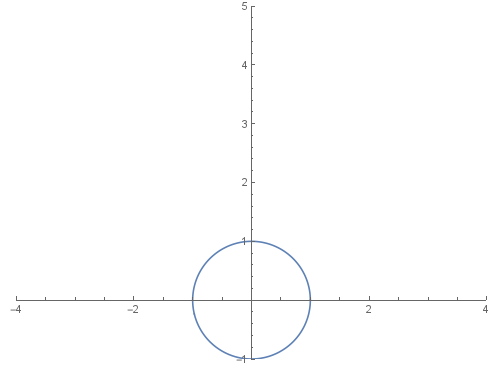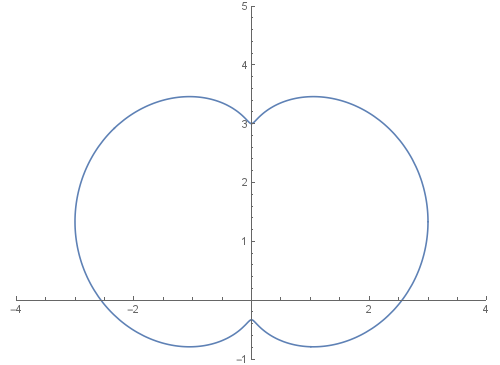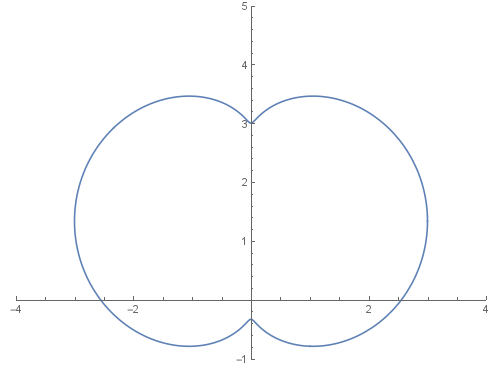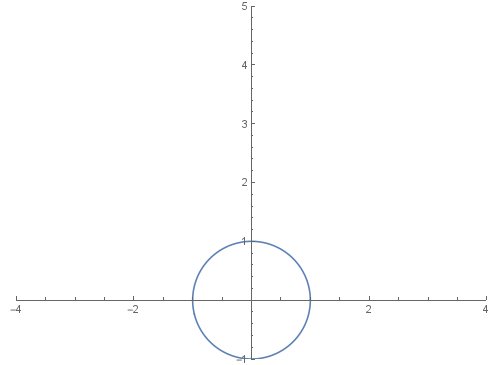
5、看看单位圆是怎么变成那另一个图形的。

z=E^(I t);a=z^3+3 z+ 2 I;

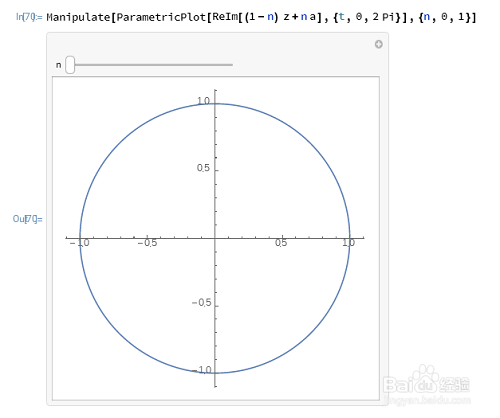
ReIm[(1-n) z+n a]的图像，随着n的变化而变化：

Manipulate[ParametricPlot[ReIm[(1-n) z+n a],{t,0,2 Pi}],{n,0,1}]