MATLAB如何实现正反傅里叶变换FFT的频域滤波？

1、教学内容

1. 系统对输入的响应(稳态)

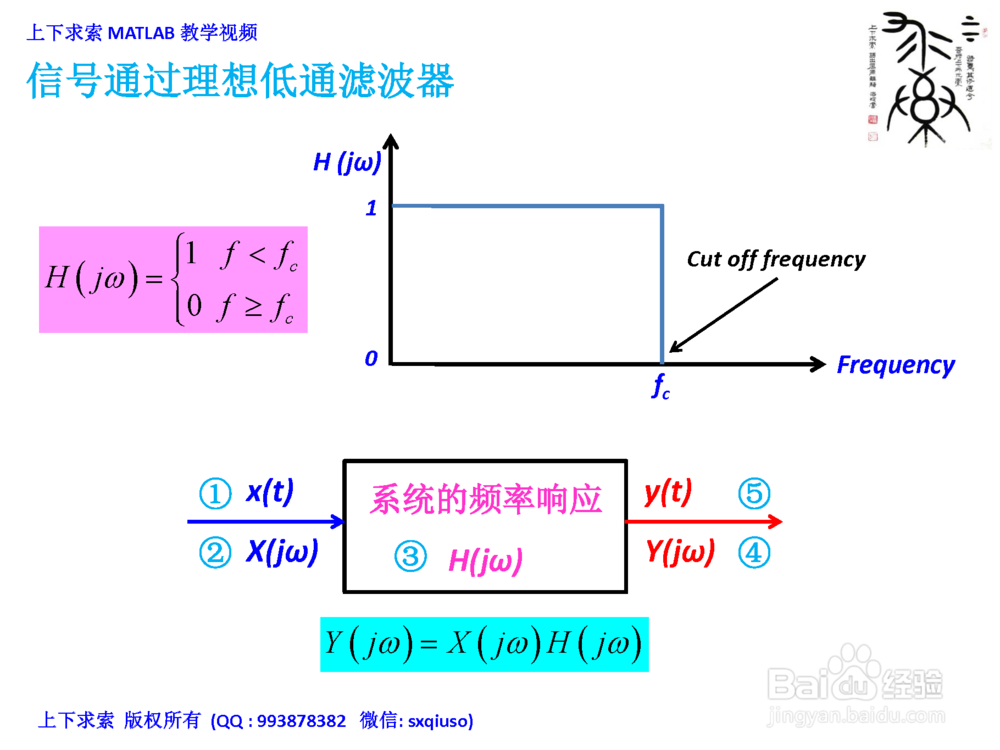
2. 信号通过理想低通滤波器

3. 信号通过RC 低通滤波器

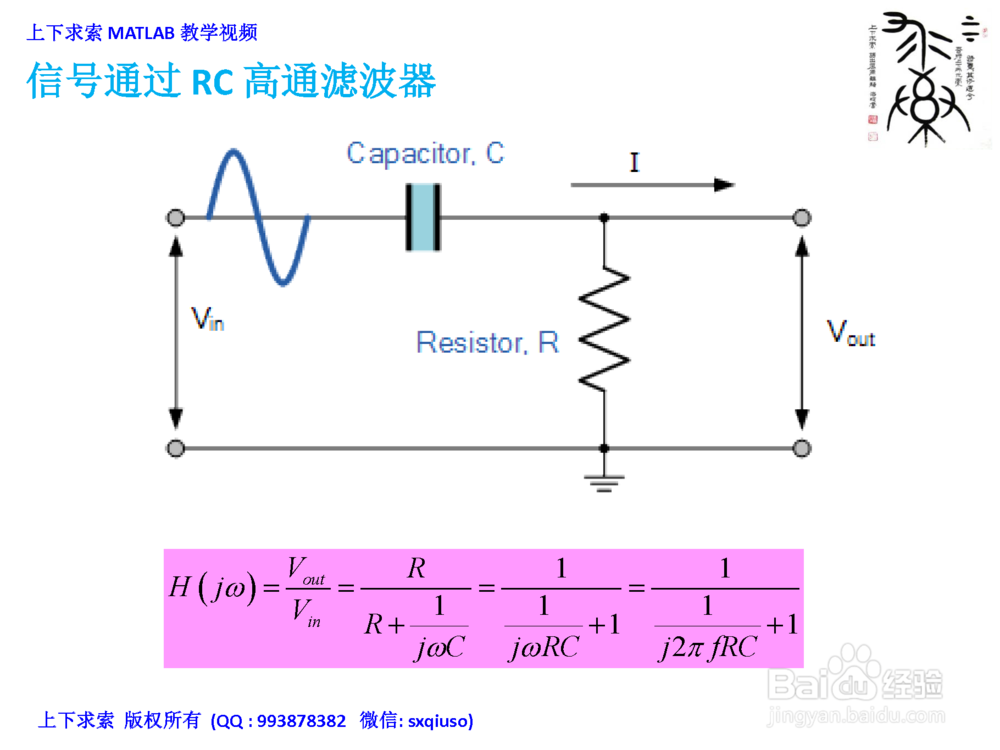
4. 信号通过RC 高通滤波器

2、系统对输入的响应(稳态)

x(t)：输入信号(时域)

X(jω)：输入信号的傅里叶变换(频域)

H(jω)：系统的频率响应

Y(jω)：输出信号的傅里叶变换(频域)

y(t)：输出信号(时域)

对Y(jω)做傅里叶反变换，得到时域输出信号y(t)

1、信号通过理想低通滤波器后，输出的时域信号

求解一个信号x(t)通过一截止频率为50Hz的理想低通滤波器后，输出的时域信号y(t)

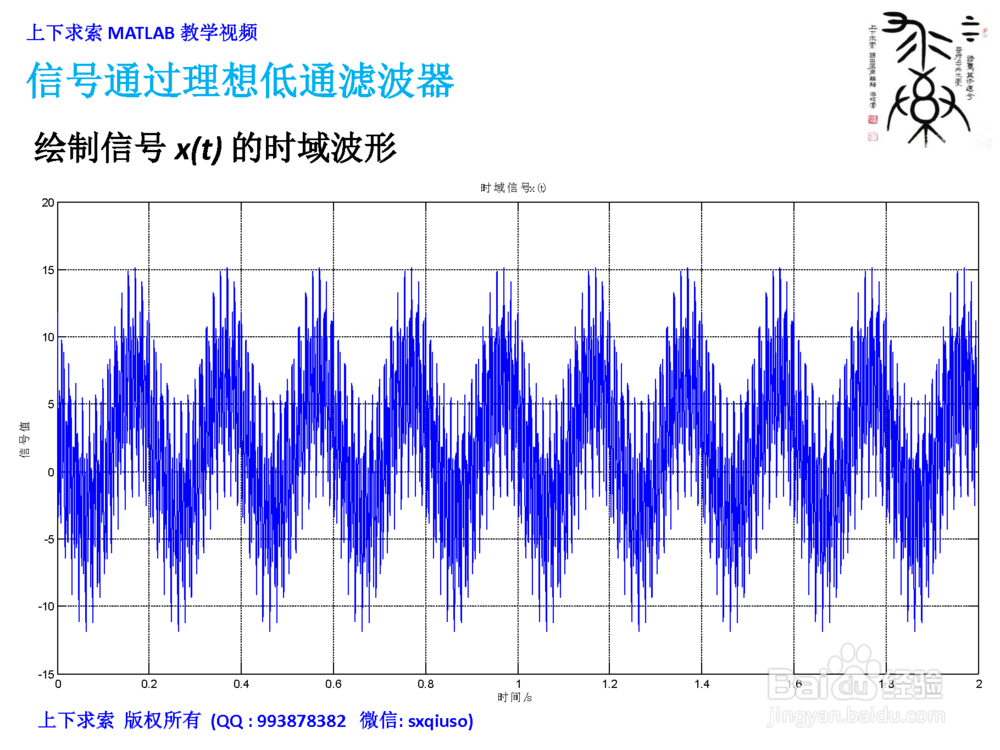
2、绘制信号FFT频谱，考察频谱的对称性

在MATLAB里绘制信号x(t)的时域波形，对信号x(t)进行FFT变换，并绘制频谱图 (实部&虚部)

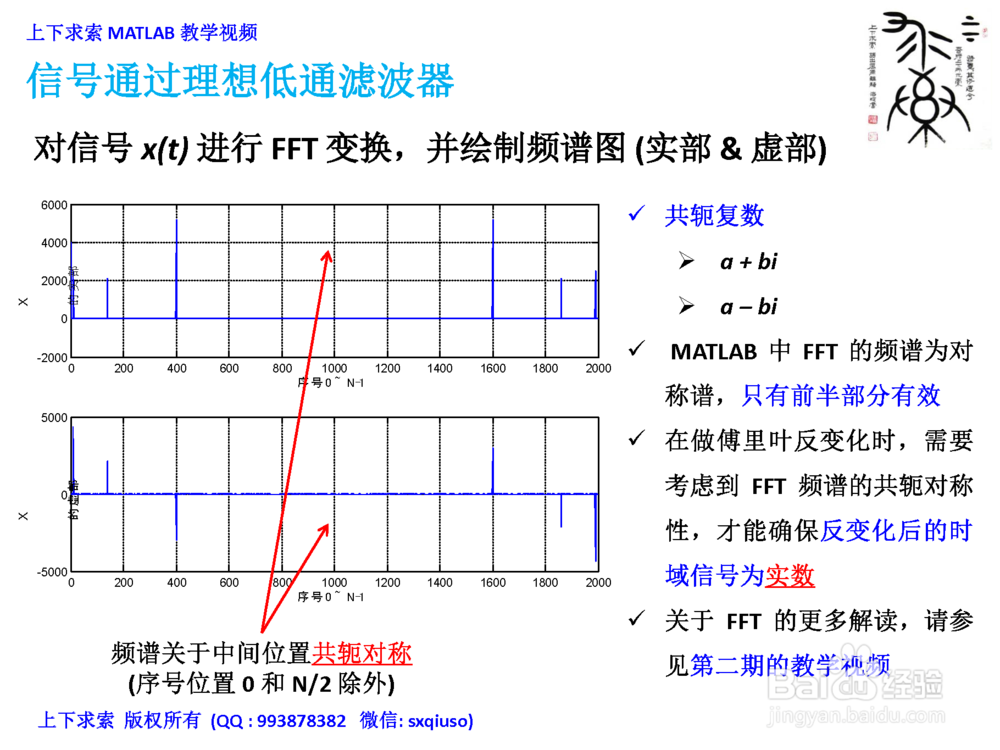
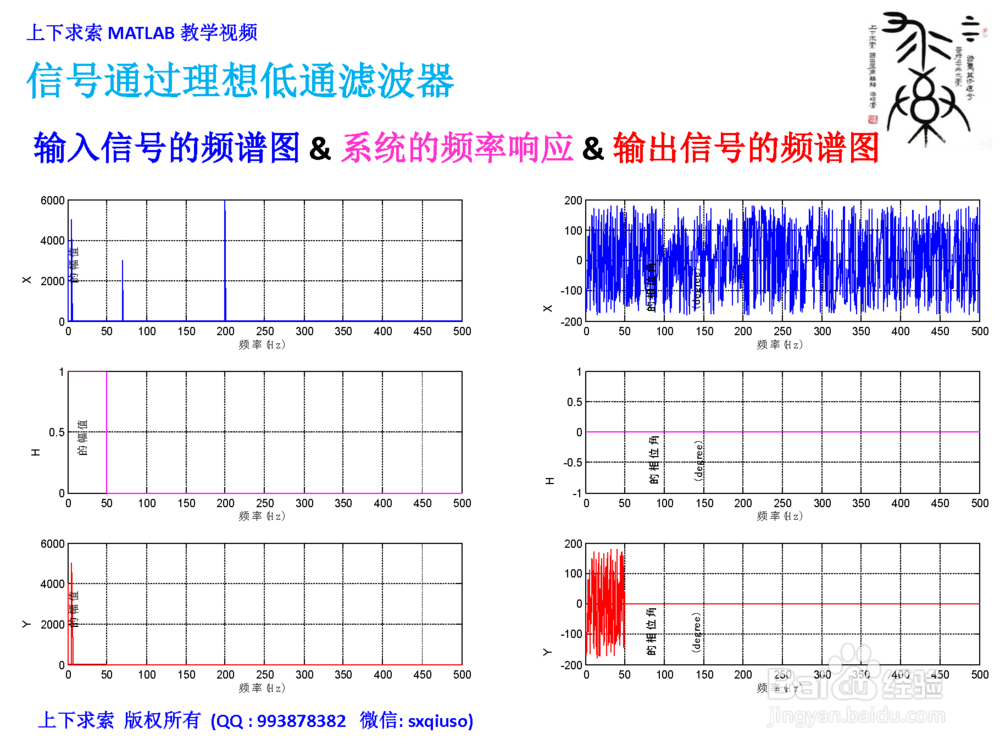
3、在MATLAB里计算并绘制

1. 输入信号的频谱图

2. 系统的频率响应

3. 输出信号的频谱图

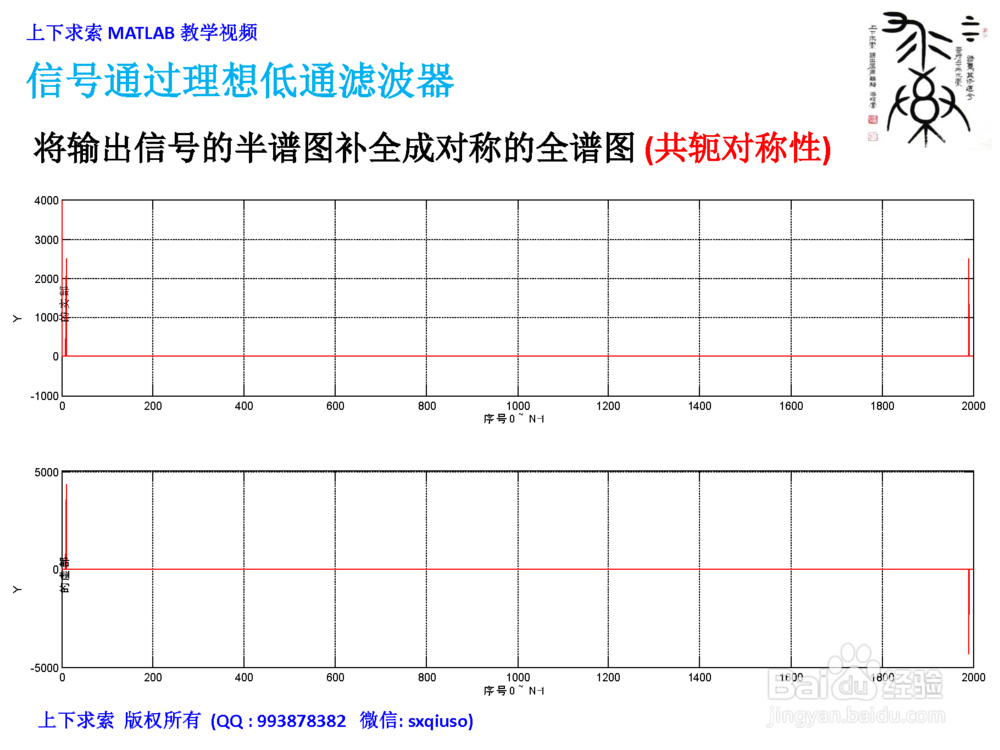
4、将输出信号的半谱图补全成对称的全谱图 (共轭对称性)

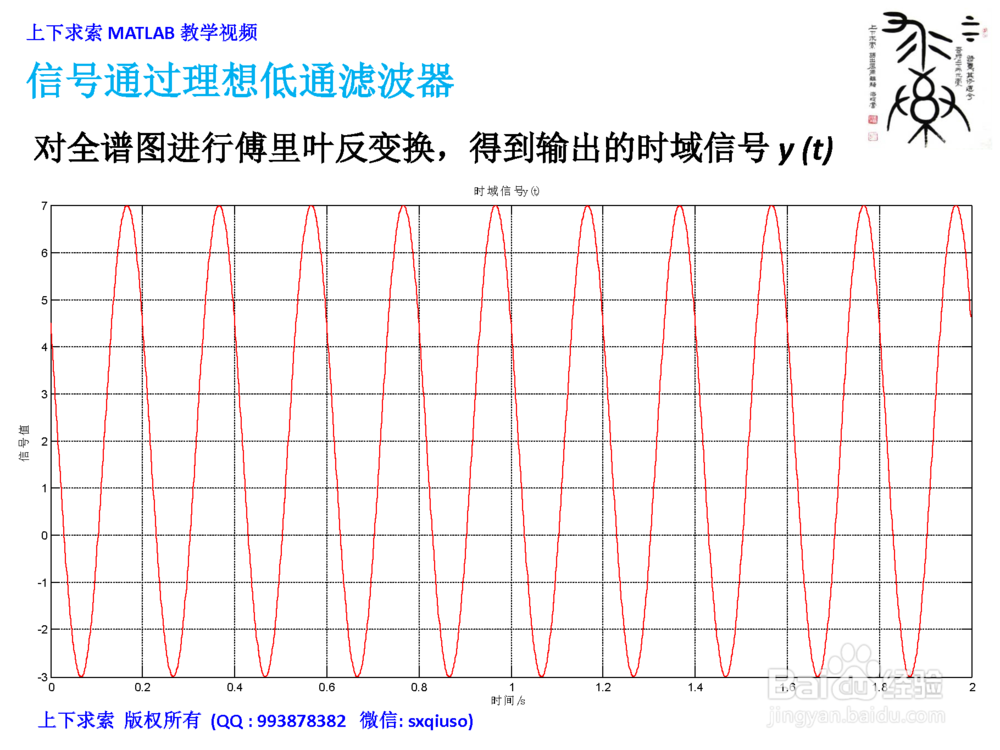
对全谱图进行傅里叶反变换IFFT，得到输出的时域信号y(t)

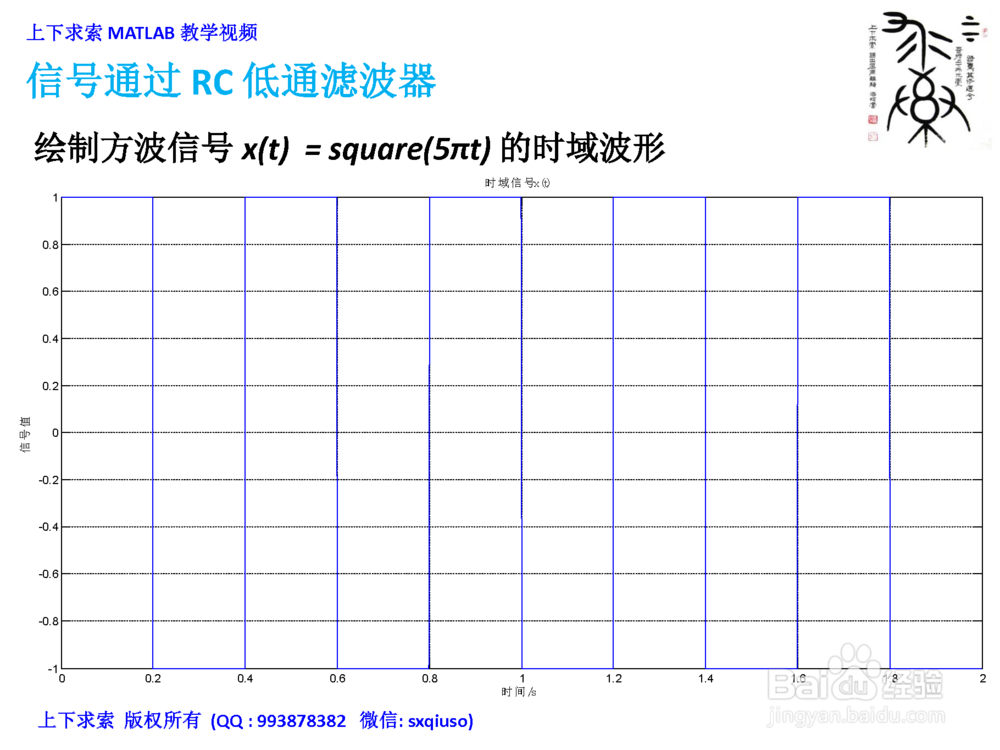
1、绘制方波信号x(t)=square(5πt)的时域波形

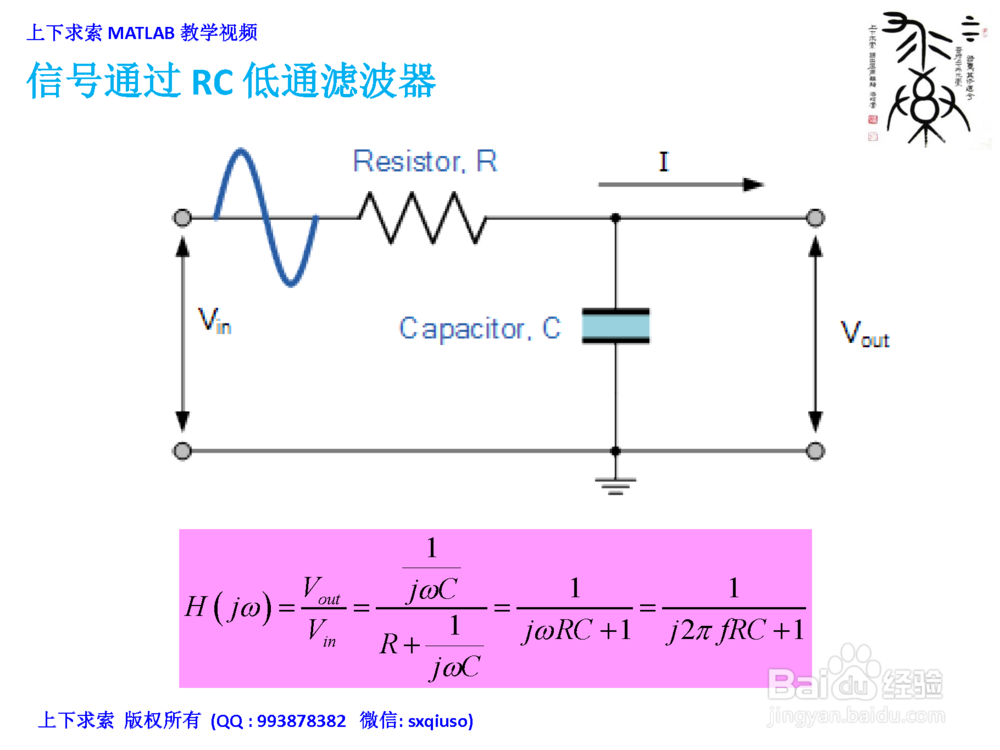
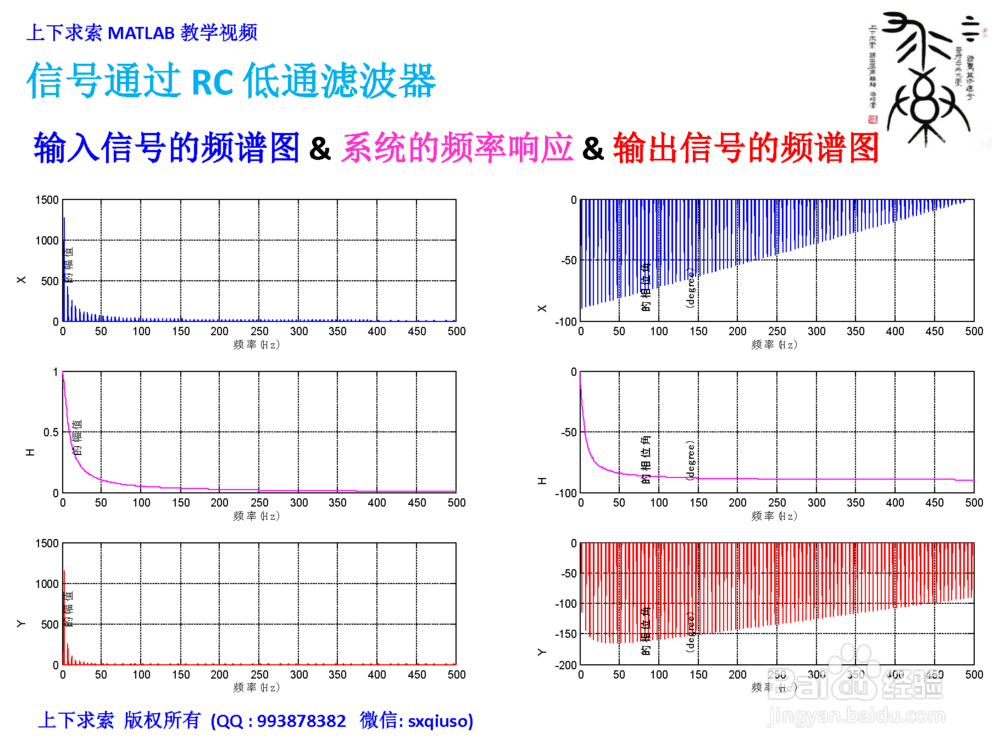
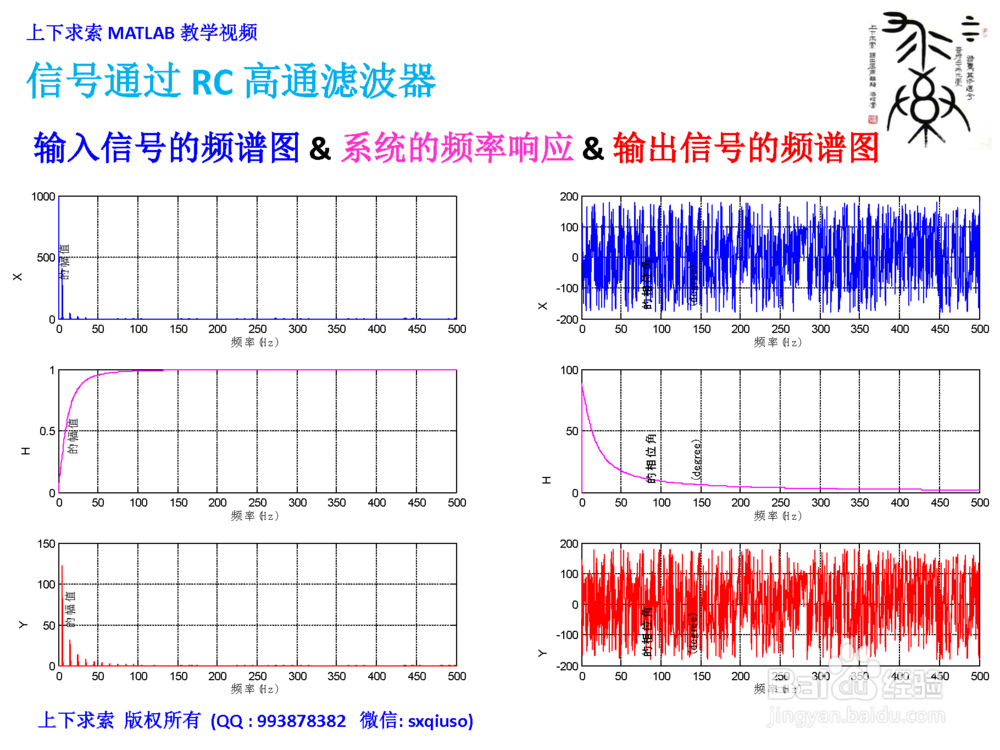
2、在MATLAB里计算并绘制

1. 输入信号的频谱图

2. 系统的频率响应

3. 输出信号的频谱图

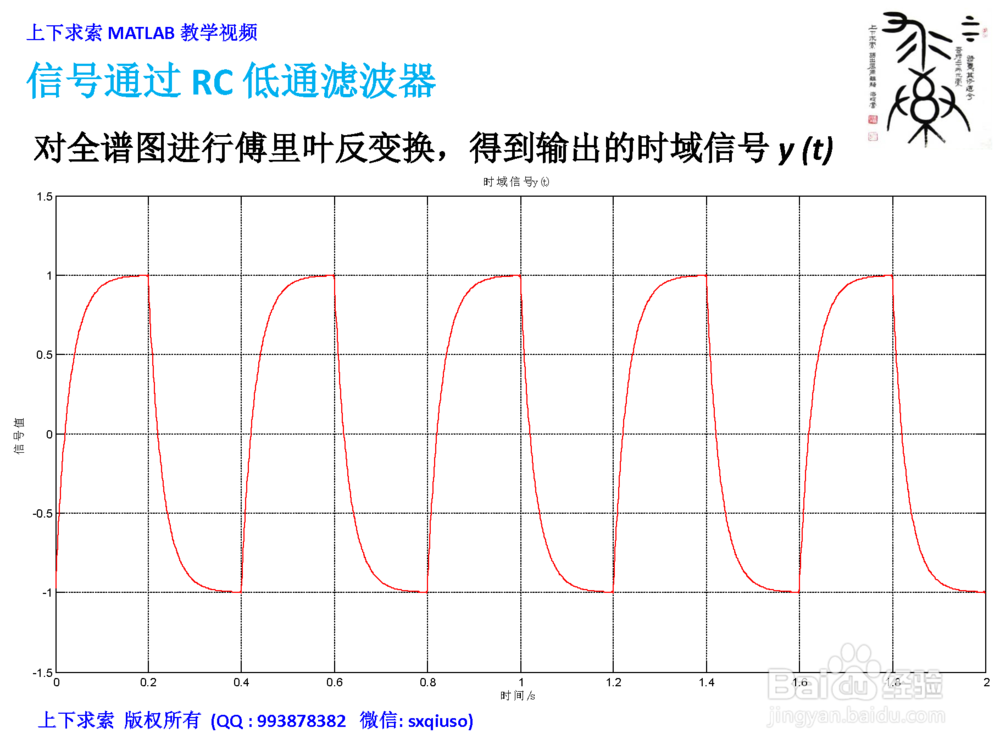
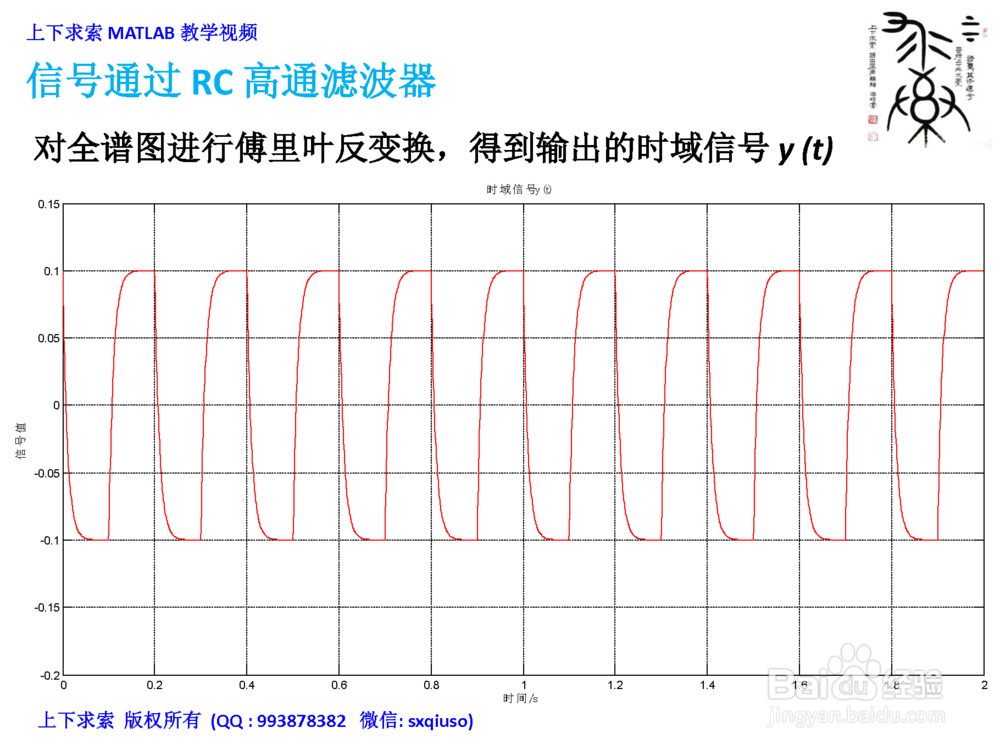
3、对全谱图进行傅里叶反变换IFFT，得到输出的时域信号y(t)

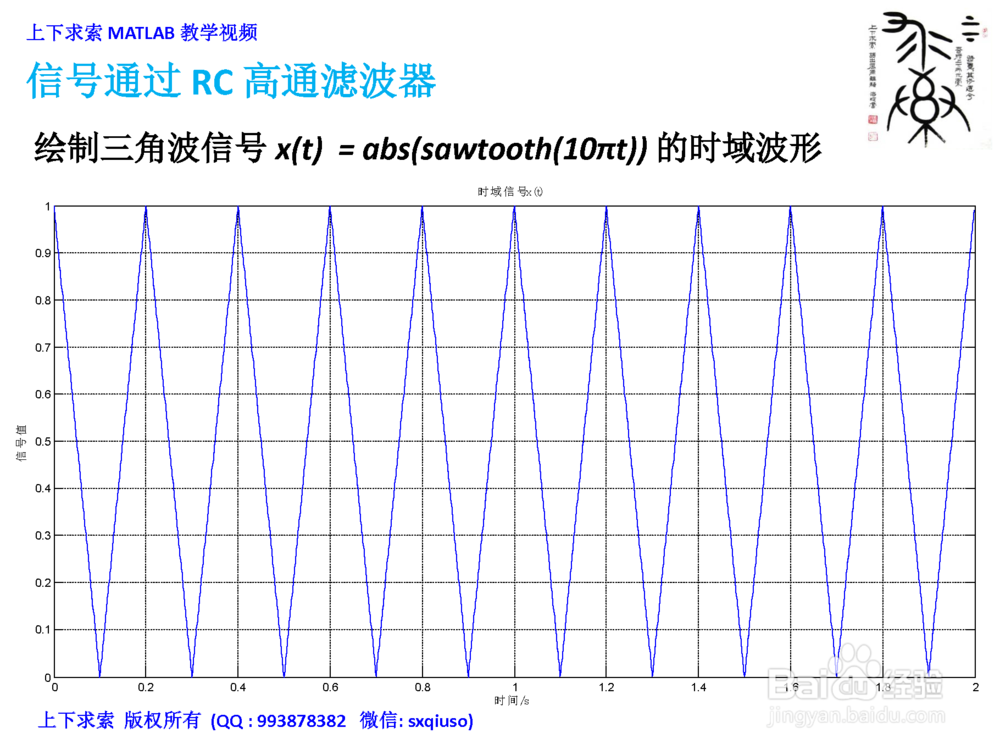
1、绘制三角波信号x(t)=abs(sawtooth(10πt))的时域波形

2、在MATLAB里计算并绘制

1. 输入信号的频谱图

2. 系统的频率响应

3. 输出信号的频谱图

3、对全谱图进行傅里叶反变换IFFT，得到输出的时域信号y(t)