等宽曲线的理解和构造

1、        举几个例子：

        等宽曲线作井口的盖子，可以保证，盖子无论怎么放置，都不会掉到井里面。

        但是，一般的井盖都是圆形的。为什么不用宽度既定而面积最小的Reuleaux三角形呢？原因是，井是圆柱形的。

2、        Reuleaux三角形

        以正三角形三个顶点为圆心、边长a为半径作圆，这三个圆的公共部分，就是Reuleaux三角形。

        Reuleaux三角形最重要的用途是，制作形状相似的钻头，可以钻出接近正方形的孔。

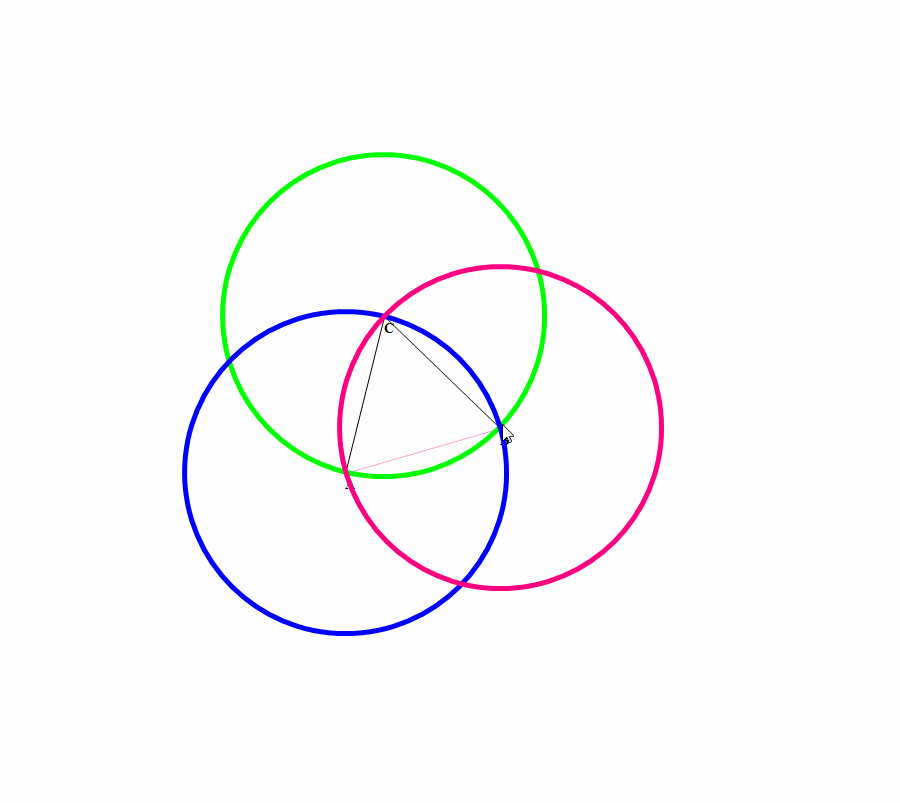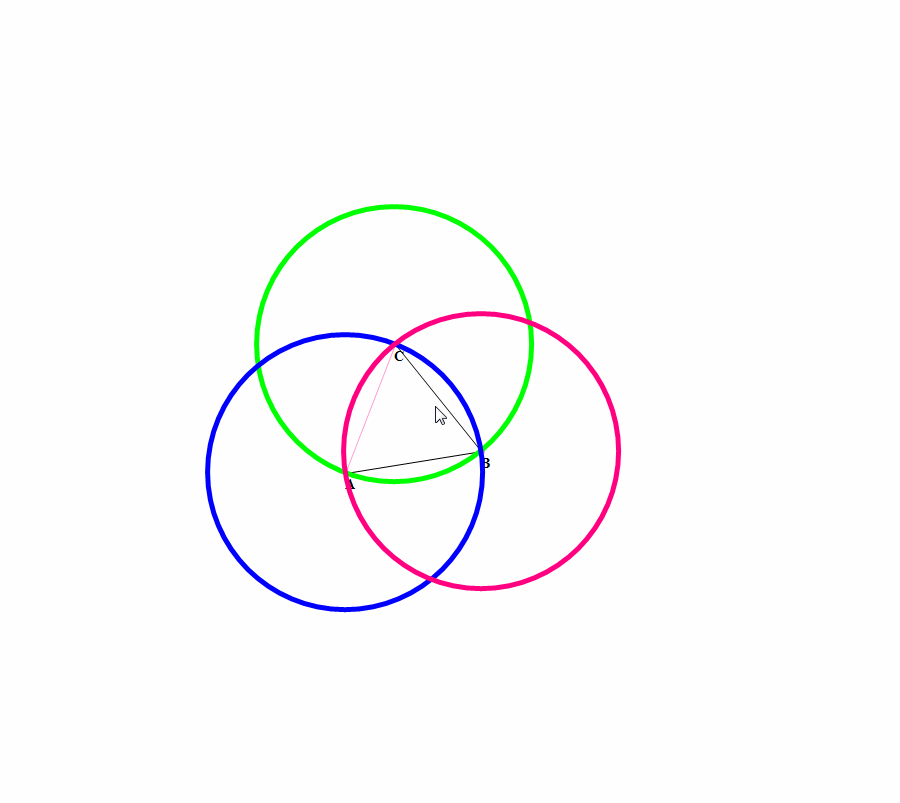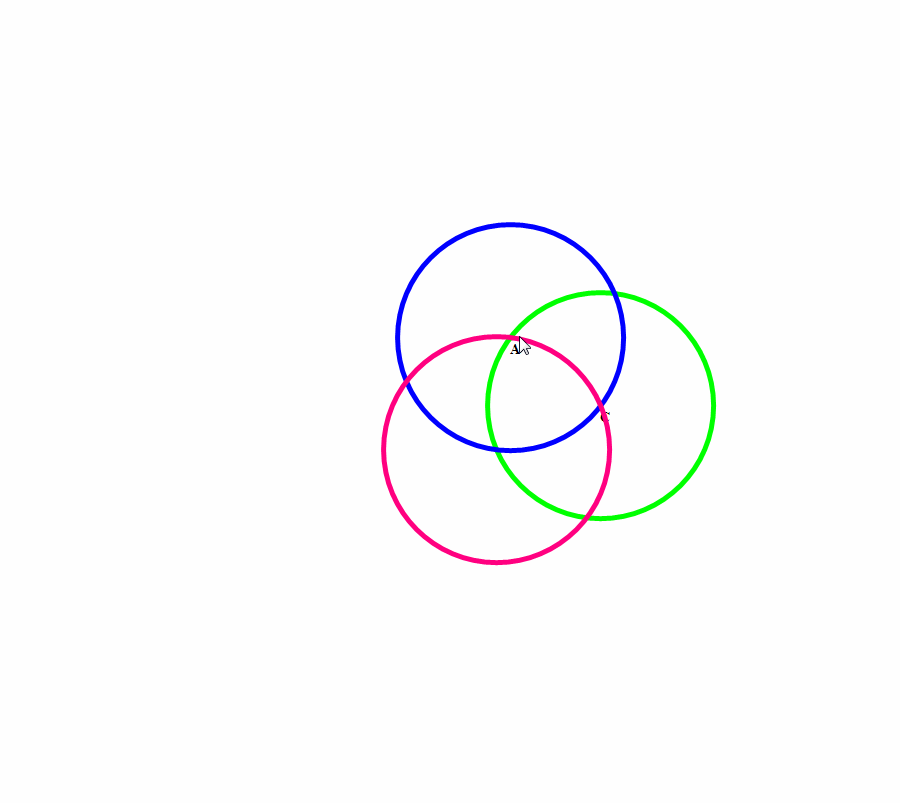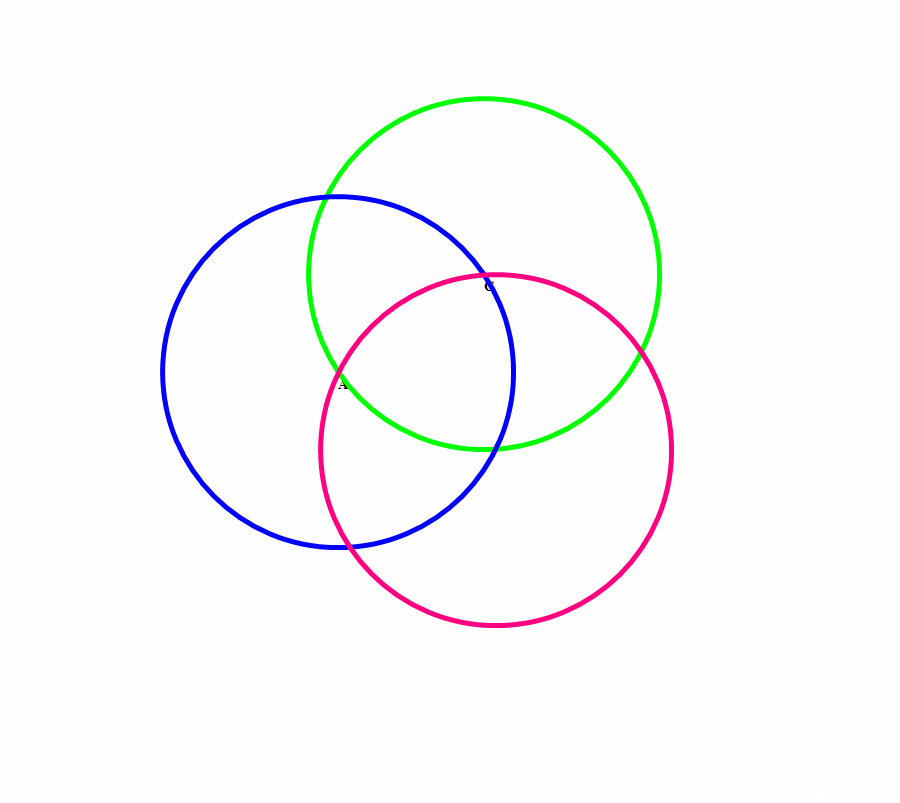
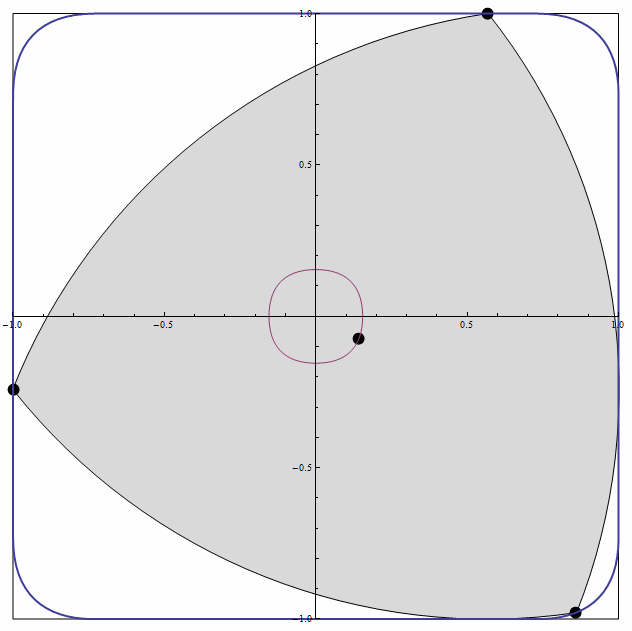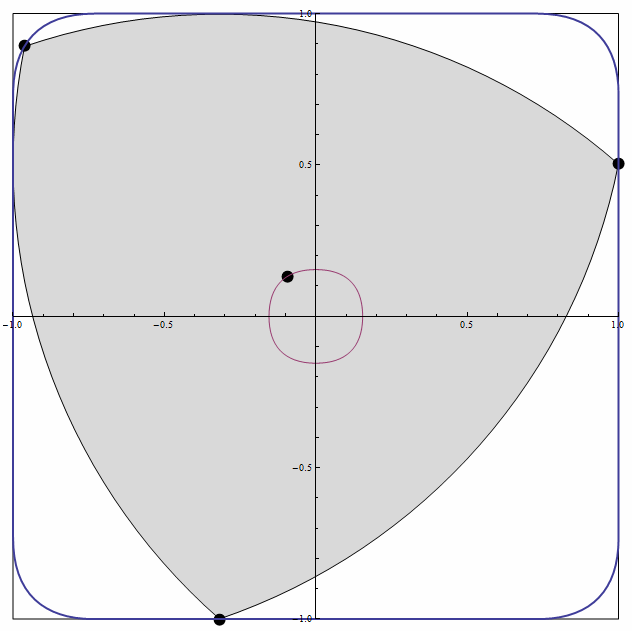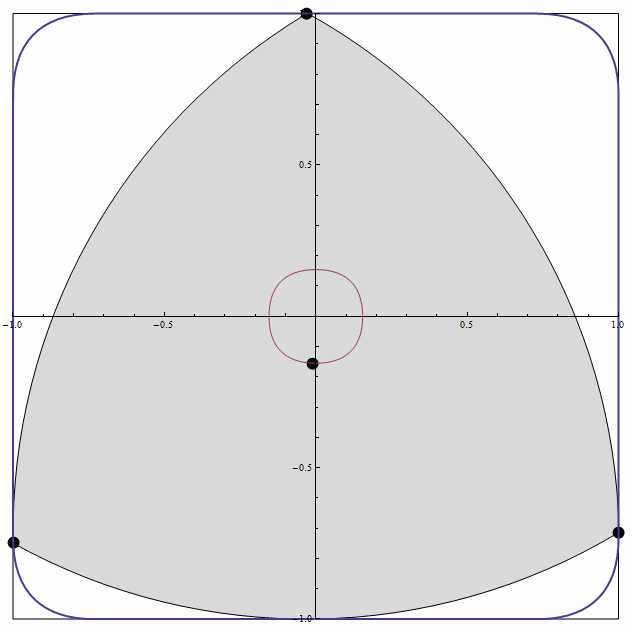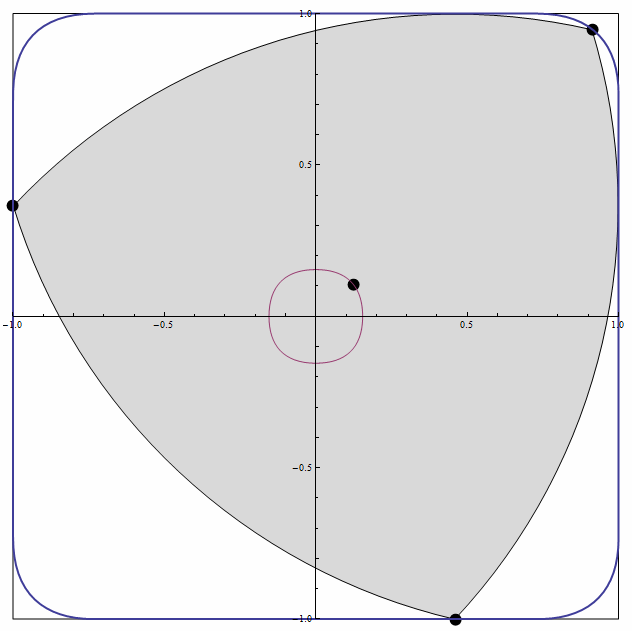
3、        把除了圆以外的等宽曲线作为自行车的车轮子，这可是闲的有毛丙？这种自行车在平坦的路面上骑行会非常颠簸，也不怕把屁股gang烂了！

        还是好好的用圆形的车轮子吧！

4、        Reuleaux多边形——边数是奇数

        先构造正2n+1边形A1A2A3······A(2n+1)，分别以2n+1个顶点为圆心、A1到A(n+1)的距离为半径作2n+1个圆，这些圆的公共部分，就是Reuleaux（2n+1）边形。

        以Reuleaux五边形为例，与它形状相似的钻头可以钻出近似正六边形的孔：

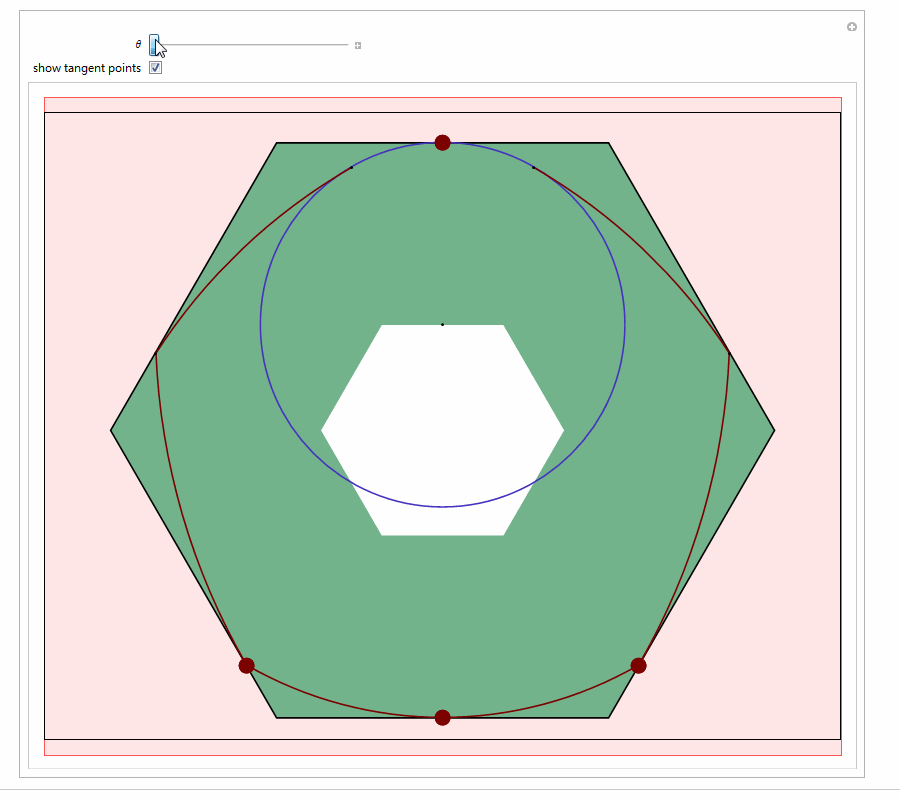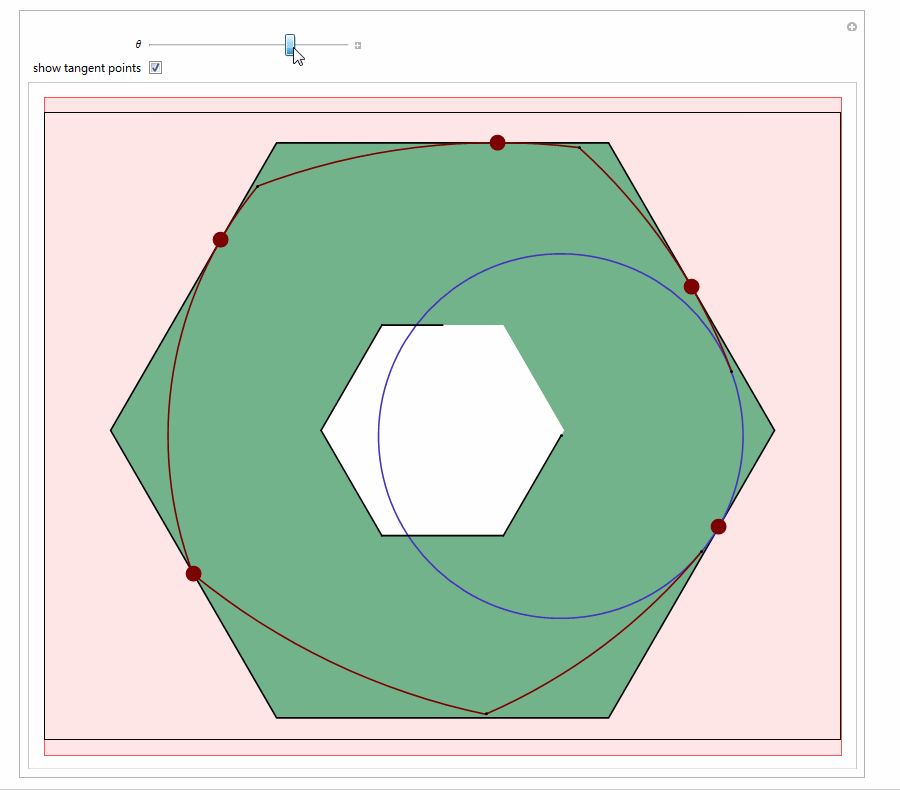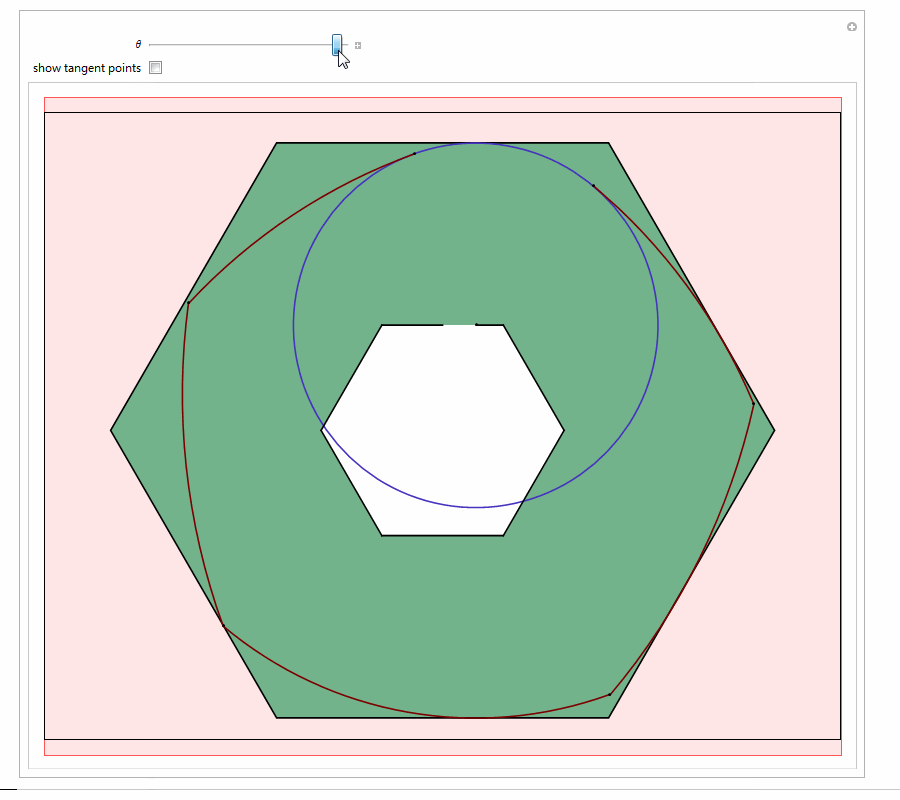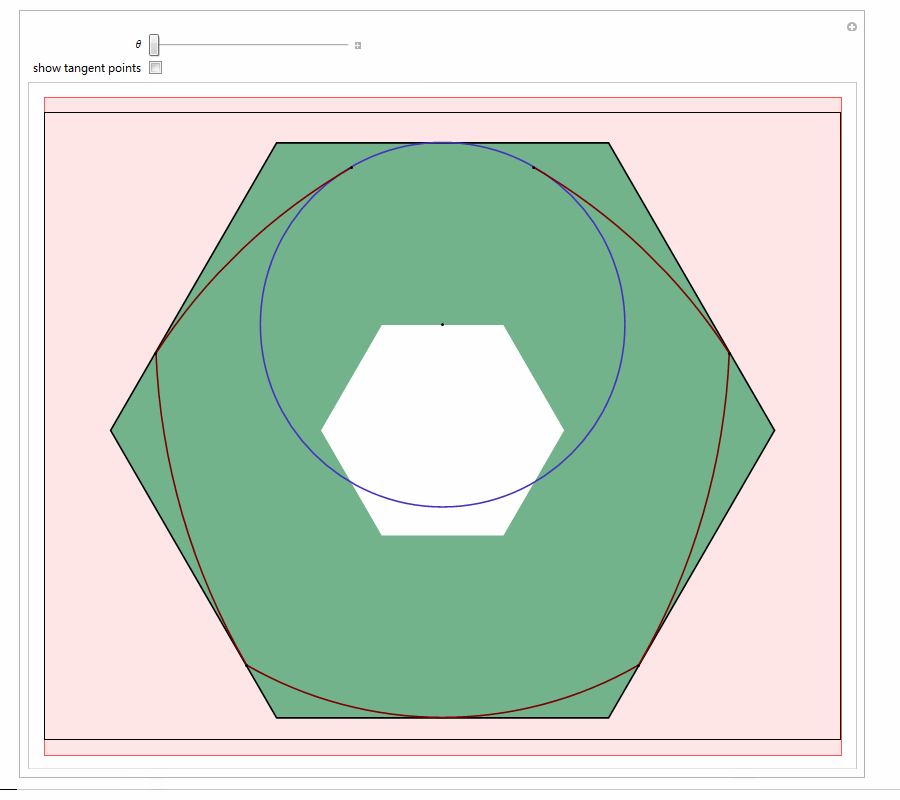
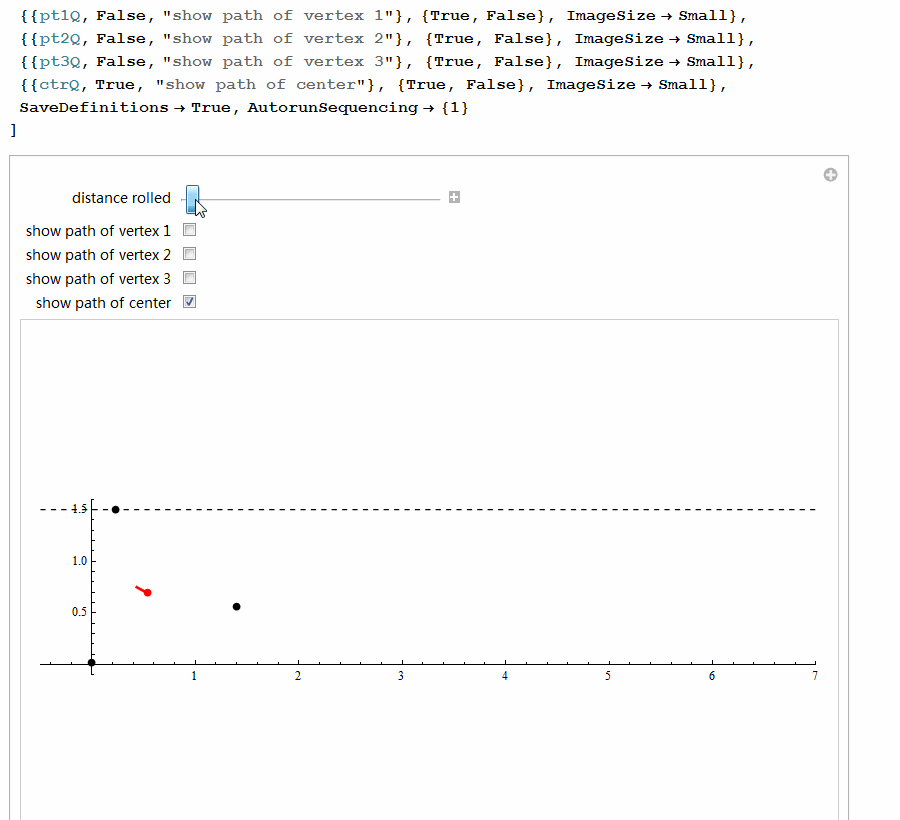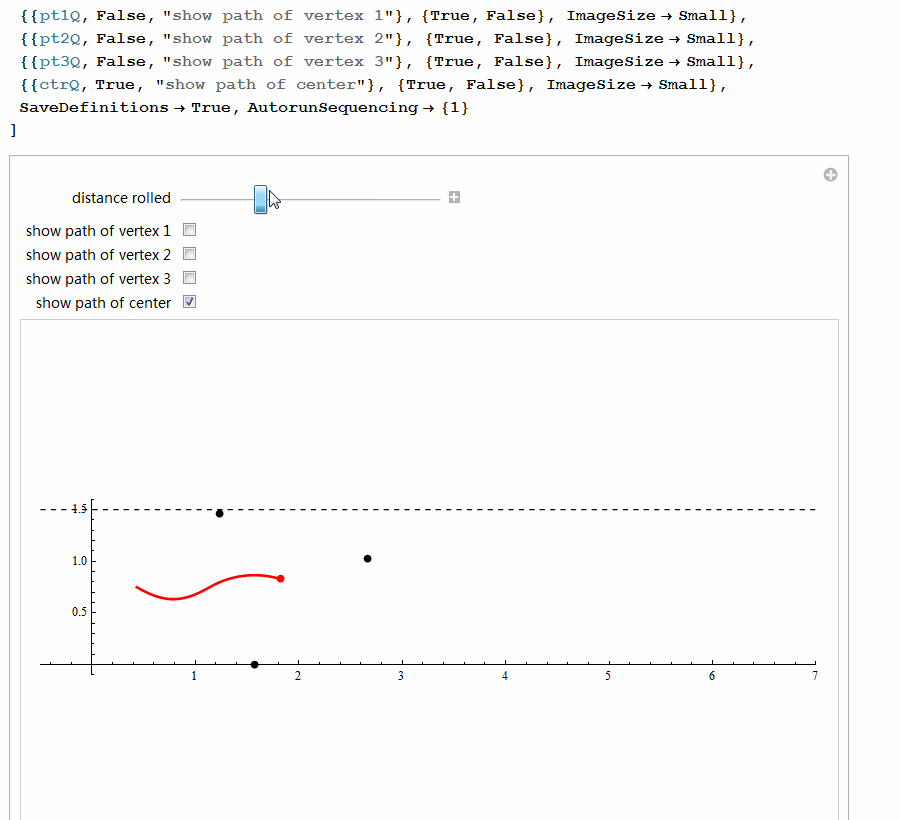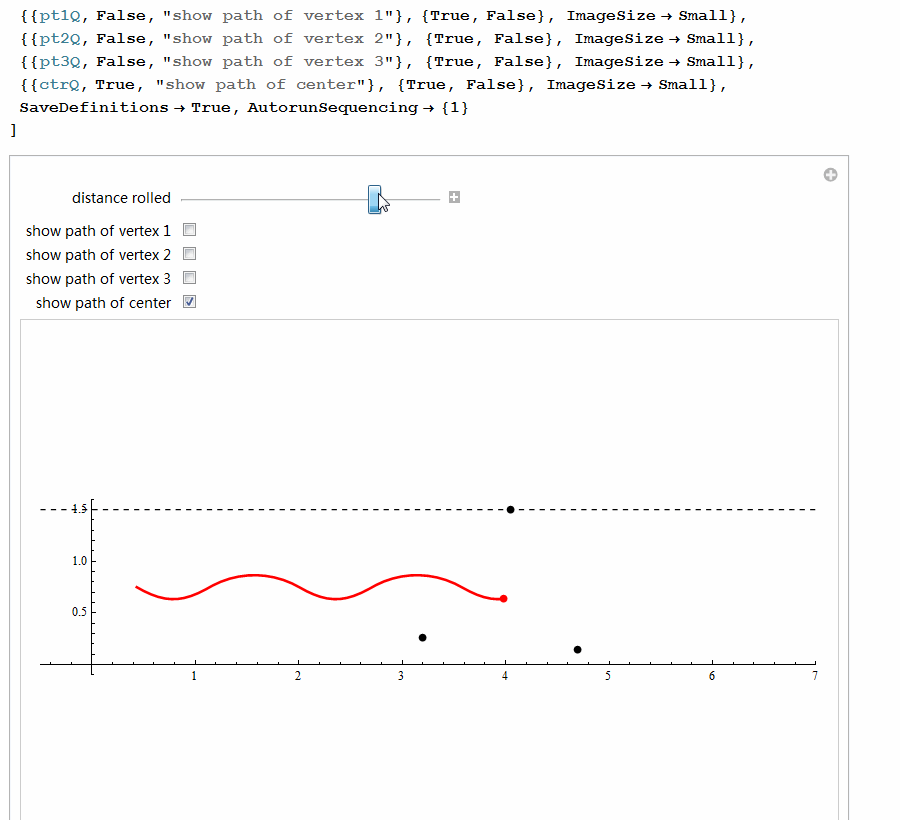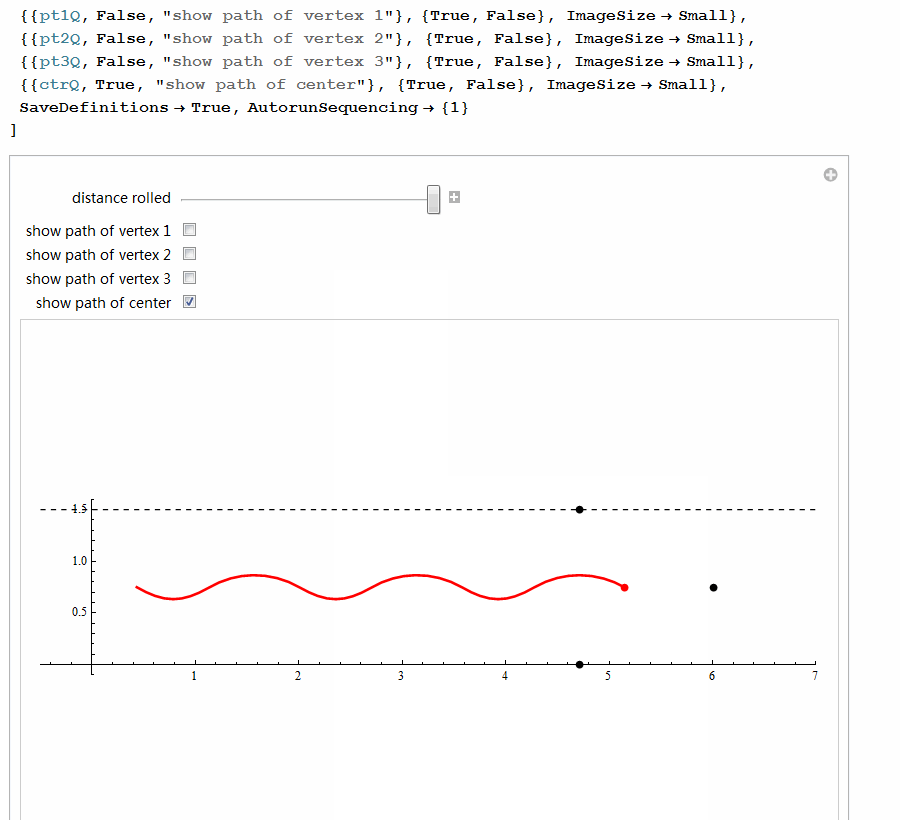
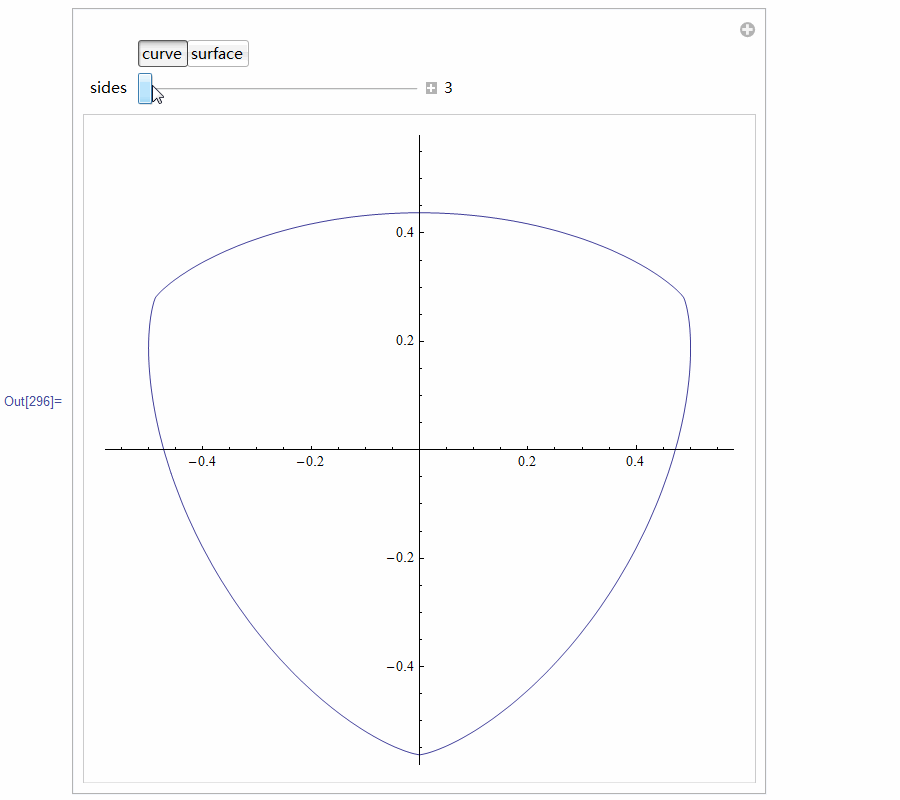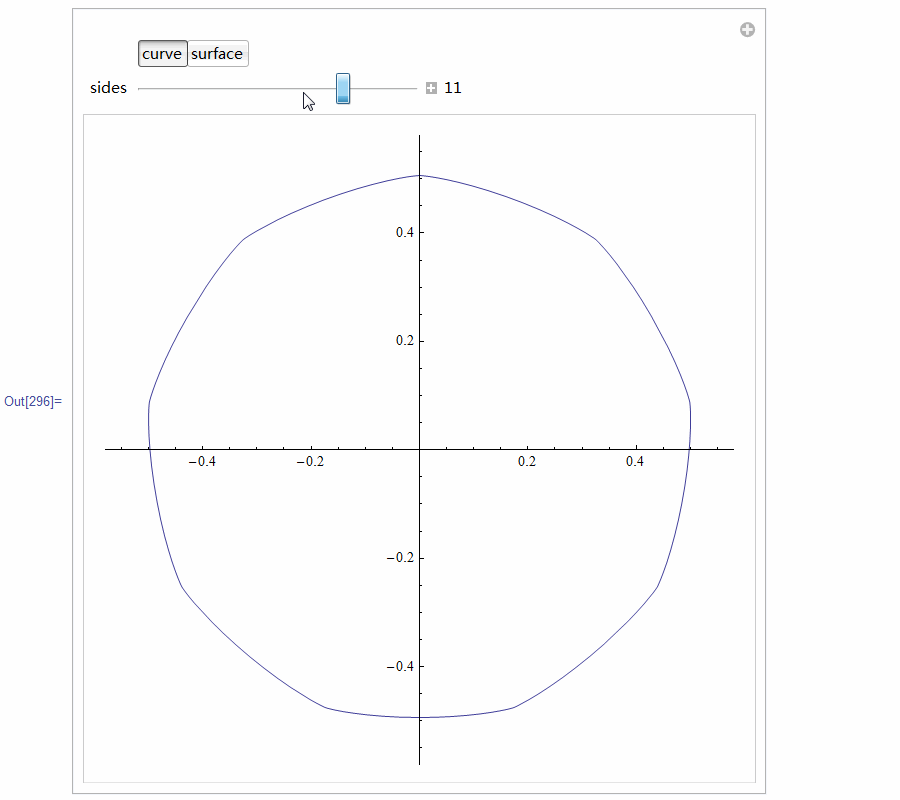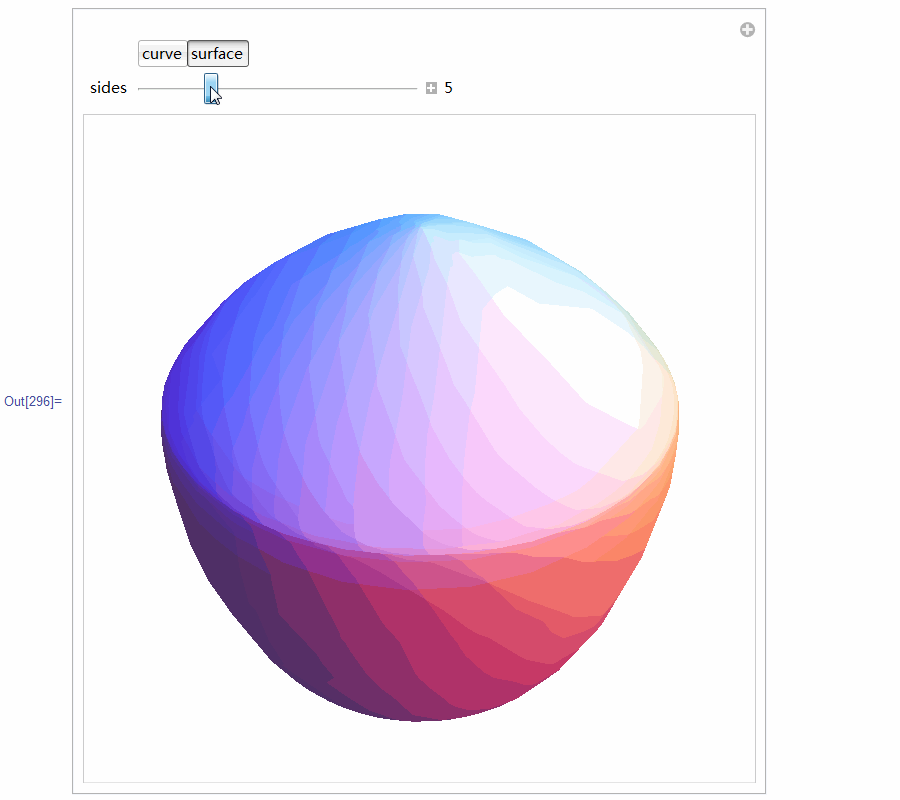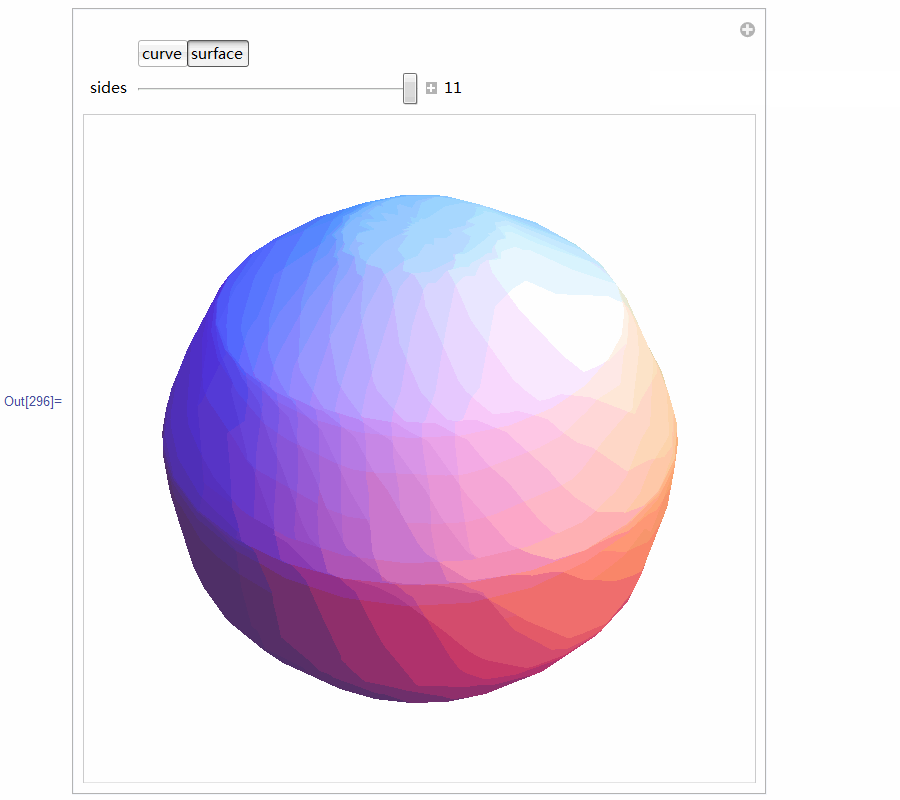
5、        用Mathematica尝试着构造等宽曲线。代码太多，截图了！

        这段代码居然构造出来等宽曲面，可是，这仅仅是等宽曲线绕对称轴的旋转体，恐怕不是等宽曲面吧？没验证过，不知道！