如何解决高中基本初等函数问题

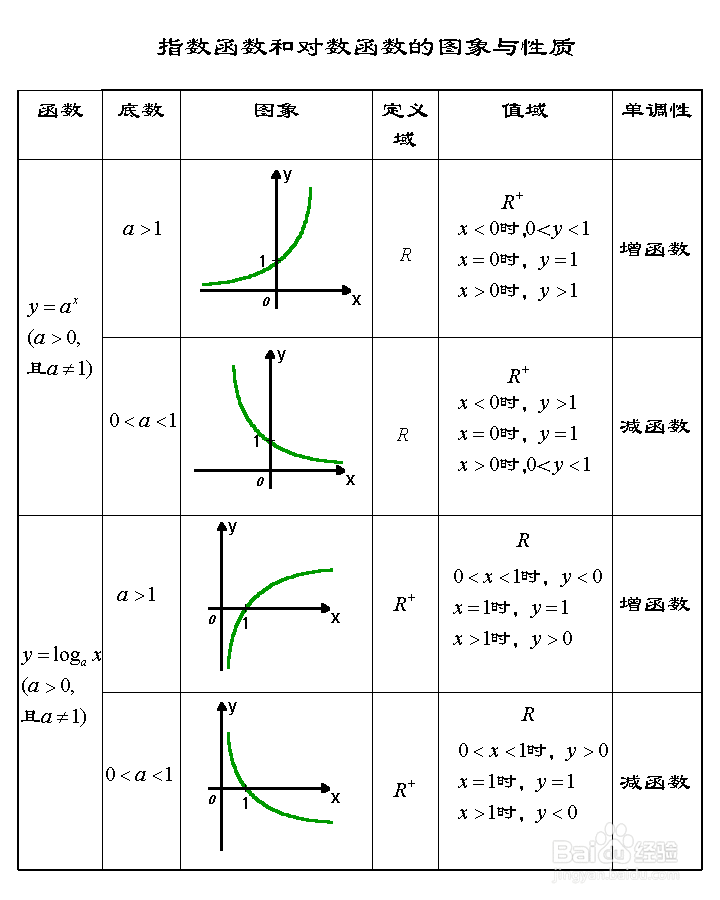
1、基本初等函数的类型、图像性质等教材上讲到就不在赘述，直接讲解例题。

例一：画出y=x²、y=x³、y=x^½、y=x^⅔的图像，部分图像如图所示。

2、最后一个y=x^⅔的图像可根据下图提供的规律，理解2/3作为分子分母的特点就能轻松画出，同时可通过代入数值检验一下。

3、例二：当x∈[-1，1]时，求函数y=3^x-2的值域.

解：首先y=3^x为单调递增函数，因为x∈[-1，1]，所以3^x∈[1/3,3]

       所以3^x-2∈[-5/3,1], 即函数的值域为[-5/3,1]

4、例三：若函数f(x)=a^x  (a>0,a≠1) 在[-1,2]上的最大值为4，最小值为m，且函数g(x)=(1-4m)√x 在[0,+∞]上是增函数，则a的值为：

解：首先要想到将a分类讨论 

当a>1时，函数f(x) 在[-1,2]上单调递增，当x=2时f(x)的最大值为4，所以a=2，当x=-1时f(-1)=2^-1=1/2为最小值, 所以m=1/2

所以g(x)=-√x，其在[0,+∞]单调递减，不符合题意

当0<a<1时，函数f(x) 在[-1,2]上单调递减，当x=-1时f(x)的最大值为4，所以a=1/4，当x=2时f(2)=(1/4)^2=1/16为最小值，所以m=1/16

所以g(x)=3/4√x，其在[0,+∞]单调递增，符合题意

综上可知，a=1/4

5、例四：已知a=㏒₂3+㏒₂√3，b=㏒₂9-㏒₂√3，c=㏒₃2，则(a+b)c的值为

解题思路：观察a、b、c的特点，a与b的底数部分相同

6、解：(a+b)c=(㏒₂3+㏒₂√3+㏒₂9-㏒₂√3)㏒₃2

                =3㏒₂3*㏒₃2

                =3(㏒₃3)/(㏒₃2)*㏒₃2

                =3

即(a+b)c的值为3