【MATLAB】利用矩阵解线性方程组
1、线性方程组的唯一解。线性方程组的形式可以表示为AX=b,其中,A为系数矩阵、X为未知数向量、b为常数项向量。该方程的唯一解应为X=A^(-1)b。
例如求解
x+2y+z=7
2x-y+3z=7
3x+y+2z=18
第一种方法是:X=inv(A)*b

2、求解
x+2y+z=7
2x-y+3z=7
3x+y+2z=18
第二种方法是:X=A\b

3、求解
x+2y+z=7
2x-y+3z=7
3x+y+2z=18
第三种方法是:X=sym(A)\sym(b)

4、求齐次线性方程组的通解。齐次线性方程组的形式为AX=0,求解的格式为:
Z=null(A,'r'),Z的列向量时方程AX=0的有理基础解系。
例如求解
a+2b+2c+d=0
2a+b-2c-2d=0
a-b-4c-3d=0

5、通解表示的程序如下
syms k1 k2
X=k1*Z(:,1)+k2*Z(:,2)

6、运行后可以将结果清楚地展现出来。

7、求非齐次线性方程组的通解。对于非齐次线性方程组的求解,有以下步骤:
1.判断AX=b是否有解;
2.求AX=b的一个特解;
3.求AX=0的通解;
4.AX=0的通解+AX=b的一个特解即为要求的结果。

8、例如求解
a+b-3c-d=1
3a-b-3c+4d=4
a+5b-9c-8d=0
建立M文件如下:

9、运行后产生结果如下:
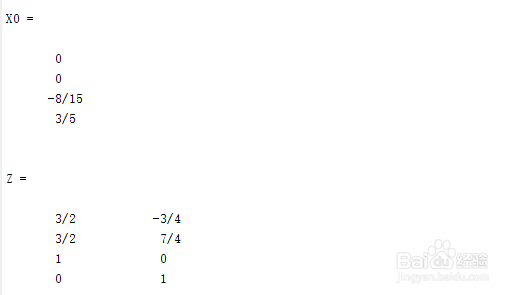
10、即可得到方程组的解
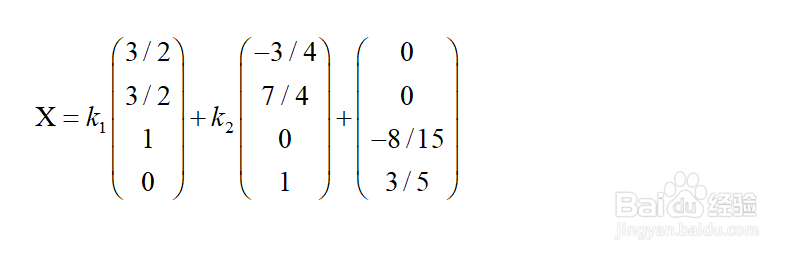
声明:本网站引用、摘录或转载内容仅供网站访问者交流或参考,不代表本站立场,如存在版权或非法内容,请联系站长删除,联系邮箱:site.kefu@qq.com。
阅读量:34
阅读量:124
阅读量:57
阅读量:150
阅读量:84