二项式常数项怎么求

1、二项式，我们约定n是非负整数，否则就没有常数项的概念了。

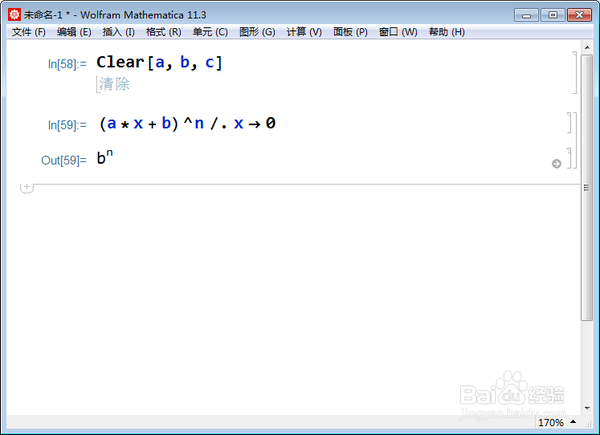
常数项，只需要令x=0，结果就是常数项：

(a*x + b)^n /. x -> 0，

答案是b^n。

2、尝试着展开二项式：

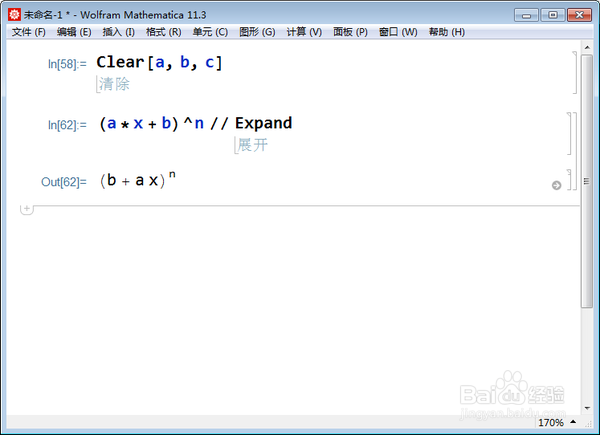
(a*x + b)^n // Expand，

没成功，原因很可能是，Mathematica没有把n当成正整数。

3、退而求其次，对n赋予具体的数值，看看能不能展开：

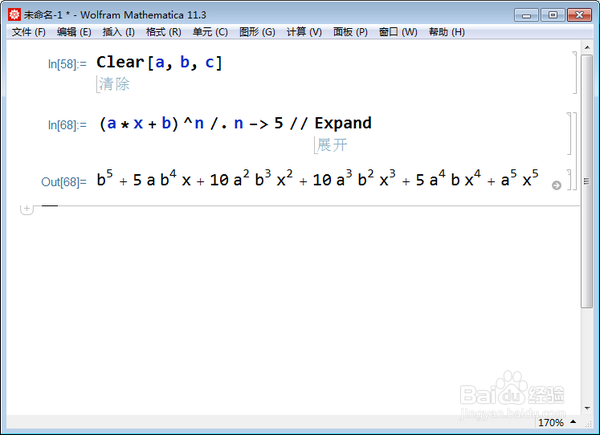
(a*x + b)^n /. n -> 5 // Expand，

展开之后，各项系数一目了然。

4、可不可以直接算出各项系数呢？试一试吧。

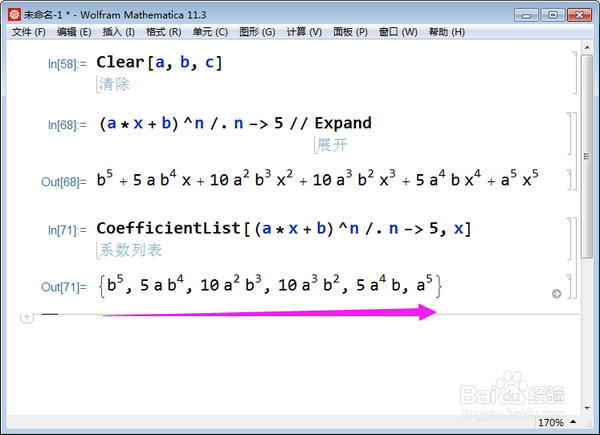
CoefficientList[(a*x + b)^n /. n -> 5, x]，

运行结果，系数是从低次项到高次项排列，第一项就是常数项。

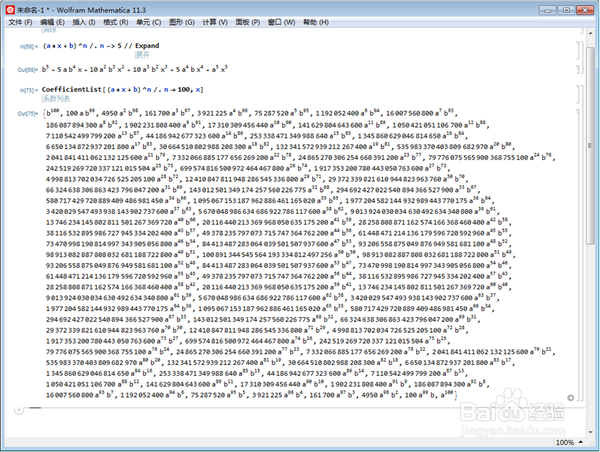
5、换一个大一点的指数：

CoefficientList[(a*x + b)^n /. n -> 100, x]，

项数多，系数长。

6、一个自然的问题是，如果不给n赋值，有没有什么办法，给出二项式各项的系数呢？

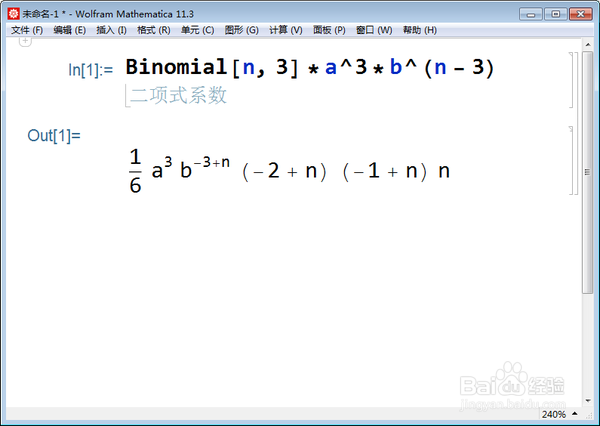
比如，计算(a*x+b)^n的三次项系数：

Binomial[n, 3]*a^3*b^(n - 3)，

这是直接套用二项式定理的结果。

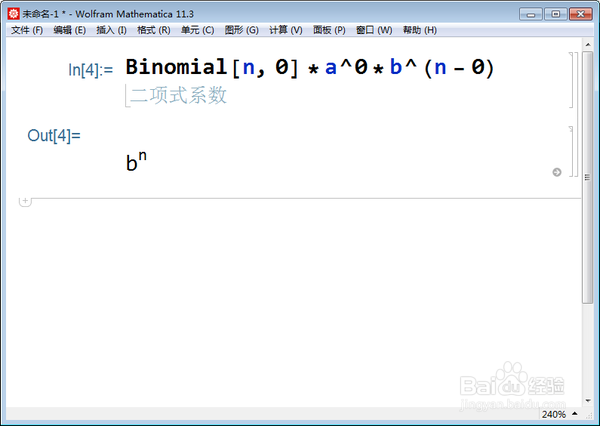
7、如此一般，可以求出(a*x+b)^n的常数项：

Binomial[n, 0]*a^0*b^(n - 0)。